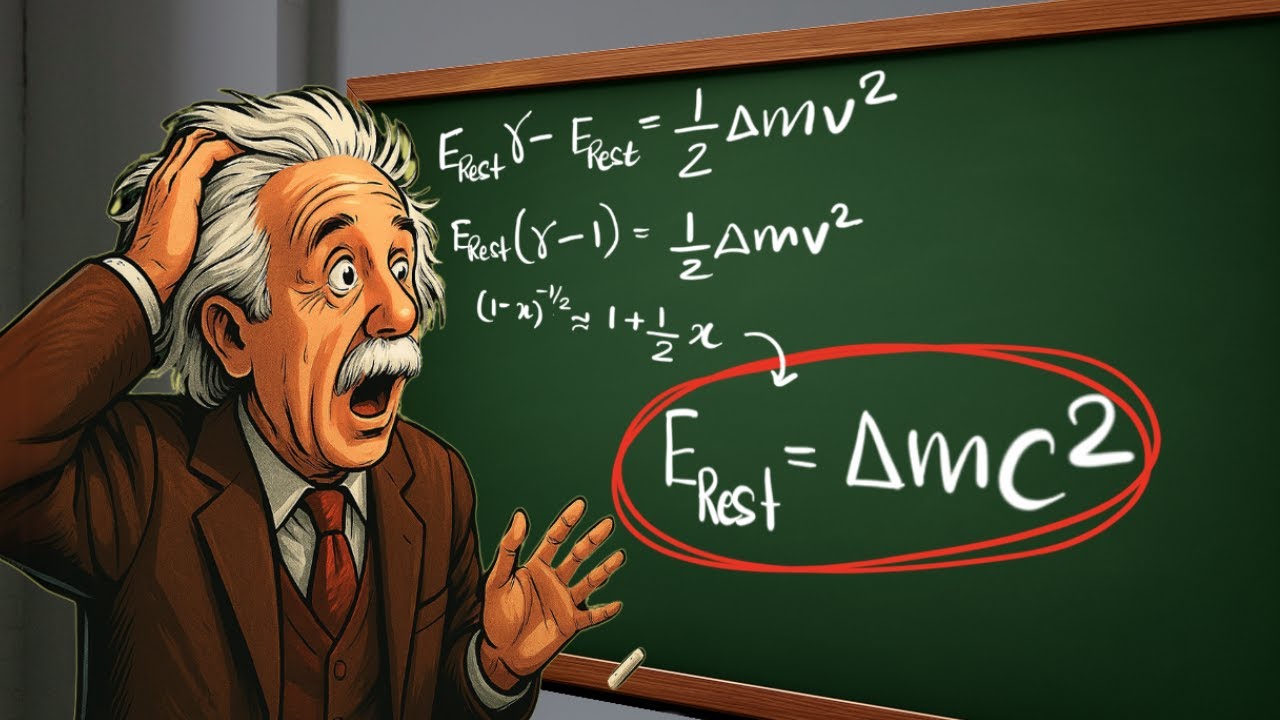Deriving Einstein's most famous equation: Why does energy = mass x speed of light squared?

Physics Explained

18 Jan 202136:48

EducationalLearning

32 Likes 10 Comments

TLDRThis video derives Einstein's famous equation E=mc^2, starting from Galilean relativity and making a key realization - if light speed is the same for all observers, their sense of time must differ. This time dilation is quantified and leads to the relativistic expressions for momentum and kinetic energy. The total energy contains a rest mass term mc^2 representing energy stored in mass. Converting mass to energy releases huge amounts, limited only by relativistic increase of mass at velocities nearing c. Finally, the relativistic energy-momentum equation underlies modern particle physics, with invariant mass measurable despite differing observer energies and momenta.

Takeaways

😲 The purpose of mechanics is to describe how bodies change position over time relative to different frames of reference.
😃 Galileo introduced the principle of relativity - laws of physics should be the same in all inertial frames of reference.
🔬 Moving clocks run slower due to time dilation - a key prediction of special relativity.
💡 The total energy of an object is equal to gamma times its rest mass energy.
🌟 E = mc^2 represents the rest energy of an object when at rest.
🚀 It would take infinite energy to accelerate a massive object to the speed of light.
😮 Massless particles like photons have momentum and energy but no rest mass.
📏 The energy-momentum relationship allows invariant mass to be calculated across frames of reference.
🔭 The discovery of the Higgs boson in 2012 relied on the energy-momentum relationship.
😃 Understanding relativity brings us closer to comprehending the mysteries of the universe.

Q & A

What is the principle of inertia?
-The principle of inertia states that a body removed sufficiently far from other bodies continues in a state of rest or uniform motion in a straight line unless acted on by an external force.
What is time dilation and how does it occur?
-Time dilation is the difference in elapsed time between stationary and moving frames of reference. It occurs due to the constancy of the speed of light - moving clocks tick slower than stationary clocks by a factor called gamma to preserve this constancy.
How is mass-energy equivalence derived?
-By considering a moving object, deriving expressions for its relativistic momentum and force, and then integrating to determine its kinetic energy. This results in the famous equation E = mc^2 relating energy and mass.
What happens as an object approaches the speed of light?
-As an object approaches the speed of light, the factor gamma approaches infinity, and therefore its energy also approaches infinity. Thus it would take an infinite amount of energy to accelerate a massive object to the speed of light.
What is the significance of the energy-momentum relationship?
-The energy-momentum relationship E^2 = p^2c^2 + m^2c^4 allows different observers to determine the invariant mass of a system based on their measured values of energy and momentum, and underlies modern particle physics.
What did the Michelson-Morley experiment demonstrate?
-The Michelson-Morley experiment showed that the speed of light is the same in all inertial reference frames, providing early evidence against the existence of a luminiferous aether and supporting Einstein's postulate of the constancy of the speed of light.
What is the difference between rest mass energy and kinetic energy?
-Rest mass energy mc^2 exists even for stationary objects and represents the energy stored in the mass. Kinetic energy depends on an object's motion and is equal to 1/2mv^2 in the low velocity limit per classical physics.
Why don't we notice time dilation in everyday life?
-In everyday situations, velocities are very small compared to the speed of light c. Therefore the factor gamma is extremely close to 1, leading to a negligible difference between moving and stationary clocks that is undetectable without precise measurements.
How did the discovery of muons provide evidence for time dilation?
-Muons produced in the upper atmosphere decay very quickly, but are detected on Earth's surface. Their lifetime is elongated by time dilation due to their high velocities, allowing the muons to reach Earth before decaying.
What is the significance of Einstein's equation E=mc^2?
-E=mc^2 shows that mass and energy are equivalent. Even a stationary object contains rest energy given by its mass. This insight enabled the discovery that mass can be converted to energy in nuclear reactions.

Outlines

00:00

ð Introduction to physics concepts, Galilean relativity and inertial reference frames

Introduces foundational concepts in physics such as motion, velocity, reference frames and the principle of inertia. Discusses Galileo's principles of relativity and the notion of inertial reference frames in constant motion where physics laws hold.

05:01

ð Adding velocities using Galileo's framework and issues when applied to light propagation

Explains the Galilean approach to adding velocities in different reference frames and brings up issues when trying to apply this framework to reconcile the experimentally measured speed of light being the same in all frames.

10:03

ð¬ Deriving how moving clocks run slower due to time dilation in Special Relativity

By considering light clocks in motion, derives the time dilation equation showing moving clocks run slower. Emphasizes all phenomena slow down in moving frames to preserve consistency per the relativity principle.

15:04

ð Why we don't notice time dilation in everyday situations with examples

Explains why time dilation due to motion is negligible at everyday speeds. Gives example calculation for Usain Bolt showing the effect is tiny until speeds approach a good fraction of the speed of light.

20:05

ð¬ Deriving the relativistic expression for kinetic energy

Step-by-step derivation of the relativistic equation for the kinetic energy of an object, culminating in the compact form K = mc^2(Î3 - 1).

25:05

ð¡ The deeper meaning and implications of E = mc^2

Provides deeper insight into the mass-energy equivalence relation E = mc^2, interpreting the rest mass energy that exists even for stationary objects and giving examples of mass-energy conversions.

30:06

ð¦ Why massive objects cannot reach the speed of light

Explains why accelerating massive objects to light speed would require infinite energy, revealing the speed of light as an absolute speed limit in the universe.

35:06

ð¡ Energy-momentum relation - the pivotal equation underpinning particle physics

Derives the famous energy-momentum equation for particles, showing it applies to both massless and massive particles. Notes this pivotal relation underlies conservation laws in particle physics.

Mindmap

Keywords

💡inertial frame of reference

An inertial frame of reference is a non-accelerating frame of reference that moves at a constant velocity. It is a key concept in Einstein's theory of special relativity, which only applies to inertial frames. The video explains that the principle of relativity introduced by Galileo states that the laws of physics should be the same in all inertial frames. An example is the train moving at a constant velocity relative to the railway track.

💡time dilation

Time dilation refers to the phenomenon that time passes more slowly for an observer who is moving relative to another observer. This is a key prediction of Einstein's theory of special relativity. The video derives the time dilation equation and shows that moving clocks run more slowly. It explains that this slowing of time is necessary so that the principle of relativity holds true.

💡speed of light

The speed of light in a vacuum is a fixed constant in physics, equal to 3 x 10^8 m/s. Einstein realized that the only way a stationary and moving observer can measure the same speed of light is if their sense of space and time is not the same. The video also explains that the speed of light represents a fundamental limit - no objects with mass can reach this velocity.

💡principle of relativity

The principle of relativity states that the laws of physics should be the same in all inertial frames of reference moving at a constant velocity relative to one another. Einstein based his theory of special relativity on this principle. The video traces this idea back to Galileo and uses it to reconcile how light can have the same speed to both stationary and moving observers.

💡mass-energy equivalence

The video shows that the rest energy of an object at rest is equal to mc^2. This famous equation expresses the equivalence of mass and energy. The video explains that this rest energy is the energy stored within an object's mass. It can be released in certain reactions, like nuclear fusion in stars or matter-antimatter annihilation.

💡relativistic mass

Relativistic mass refers to the mass of an object when it is moving at relativistic velocities near the speed of light. The video shows that the total energy of a moving object can be written as gamma*mc^2, where gamma depends on the object's velocity. An object's relativistic mass increases as its speed approaches c.

💡relativistic momentum

The classical equation for momentum (p = mv) must be modified in Einstein's theory to correctly describe objects moving at relativistic velocities. The video derives an expression for the relativistic momentum, which depends on the object's rest mass, velocity, and the factor gamma.

💡relativistic kinetic energy

Like momentum, the classical kinetic energy equation must also be revised to account for relativistic effects. The video shows how to calculate the work done on an accelerating relativistic object to derive an expression for its kinetic energy.

💡energy-momentum relation

One of the key equations in modern physics that connects the energy, momentum, and mass of particles and objects. The video shows how squaring the relativistic energy equation leads to this famous E^2 = (pc)^2 + (mc^2)^2 expression. It explains why this relation is invariant across observers.

💡 invariance of the speed of light

A core assumption of Einstein's theory of special relativity is that speed of light in vacuum is the same for all inertial observers, regardless of their relative motion. The video grapples with how this can be consistent with the expected addition of velocities. It concludes only with a differing sense of space and time can c remain invariant.

Highlights

Derives the famous mass-energy equivalence equation E=mc^2 using relativistic mechanics and the principle of relativity

Explains the meaning of inertial frames of reference and their importance in special relativity

Demonstrates time dilation - how time passes slower in moving frames of reference

Verifies time dilation using the decay of high speed muons created in the upper atmosphere

Shows the total energy of an object is equal to gamma times the rest mass energy

Interprets E=mc^2 as the rest energy that exists even for stationary objects

Explains how mass can be converted to energy during nuclear processes

Determines that infinite energy is required to accelerate a massive object to the speed of light

Shows that the momentum of a massless photon is proportional to its energy

Derives the famous relationship between energy, momentum and mass

Explains how the invariant mass allows different observers to agree on properties

Notes that the higgs boson mass was determined by the energy-momentum relation

Encourages curiosity and questioning to comprehend the mysteries of nature

Aims to help comprehend a little of the mystery of relativity each day

Derives key equations of special relativity from first principles using thought experiments

Transcripts

Browse More Related Video

Why does E=MC²?

Why speed of light results in E = mc^2 ? [Einstein's original proof]

Special Relativity | Lecture 3

How can a photon have momentum?

Kinetic Energy EXPLAINED in 5 Levels - Beginner to Advanced (Classical Physics by Parth G)

Why light has energy, but no mass? (Understanding E = mc2)