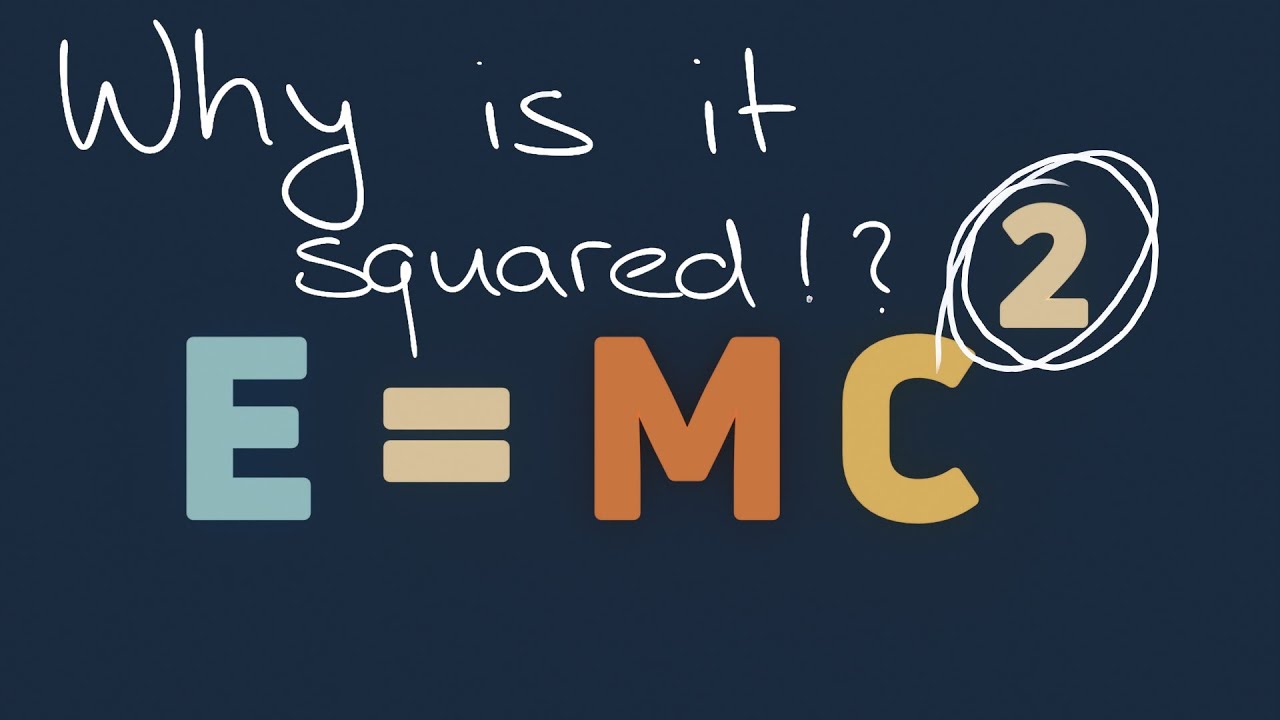Why speed of light results in E = mc^2 ? [Einstein's original proof]
TLDRThe video script presents an intuitive derivation of Einstein's mass-energy equivalence principle, E=mc². It begins with a thought experiment involving a radioactive atom emitting photons and uses the concept of the Doppler effect to explain how the energy loss from the atom is related to a change in its mass. The script then applies the principles of special relativity, including time dilation and the relativistic Doppler effect, to show that the energy of the photons as observed from a moving frame is greater than in the rest frame. This leads to the conclusion that the lost energy corresponds to the lost mass, thus confirming the famous equation E=mc², highlighting the interplay between energy, mass, and the speed of light.
Takeaways
- 🌟 Einstein's thought experiment on a radioactive atom losing energy by emitting two photons leads to the concept of mass-energy equivalence.
- 🚀 The constant speed of light and the emission of photons in opposite directions are crucial to understanding the lack of recoil on the atom.
- 🧠 The perspective from a moving rocket reveals additional kinetic energy and Doppler effect on the frequencies of the emitted photons.
- 💡 The Doppler effect causes a difference in observed photon energies between the stationary and moving frames, leading to the conclusion that energy loss equals mass loss.
- 📐 The historic derivation of E=mc² is showcased through a step-by-step visualization of the necessary math from scratch.
- 🌈 The blue-shifted and red-shifted photons have different energies due to the Doppler effect, which is a direct result of the source's motion.
- 🔄 The relativistic Doppler effect calculation involves taking into account time dilation and the change in wavelength due to the motion of the source.
- 📈 The total energy of the photons in the moving frame is found to be higher than in the rest frame, which necessitates a loss of mass from the atom.
- 🌌 The lack of a medium for light is key to observing the Doppler effect on photon energies, unlike sound waves which require a medium and do not exhibit this discrepancy.
- 📊 The mathematical approximation of the Doppler effect for low velocities involves a first-order expansion, simplifying the complex equations into a more manageable form.
- ✨ The video script provides an intuitive understanding of the derivation of E=mc², making a complex concept accessible and engaging for the audience.
Q & A
What is the main concept discussed in the video?
-The main concept discussed in the video is the derivation of the mass-energy equivalence principle, E=mc², through an intuitive explanation of Einstein's thought process in 1905.
How does the video begin its explanation of E=mc²?
-The video begins by asking us to imagine a radioactive atom with 10 units of energy that emits two photons of light, each carrying one unit of energy, and explores the consequences of this process from different reference frames.
What role does the constant speed of light play in the derivation?
-The constant speed of light is crucial as it leads to the conclusion that the atom must have lost mass equivalent to the energy it emitted, as the speed of light does not change in any reference frame, resulting in the mass-energy equivalence principle.
Why does the video mention two photons being emitted in opposite directions?
-Two photons are emitted in opposite directions to ensure that the atom remains at rest and does not recoil, allowing for a clear demonstration of the mass-energy relationship without the complexity of momentum considerations.
How does the rocket's reference frame change the perceived energy of the atom?
-From the rocket's reference frame, the atom appears to be moving, and thus it is assigned additional kinetic energy. This results in the calculation of the atom's energy being 8 units plus half of the product of the mass and the square of the velocity (MV²).
What is the significance of the Doppler effect in this explanation?
-The Doppler effect is significant because it shows that the frequency of light changes depending on the relative motion between the source and the observer, which leads to a difference in the perceived energy of the photons and ultimately to the conclusion that energy loss equates to mass loss.
Why does the video emphasize that light does not require a medium for propagation?
-The video emphasizes this point because it is the lack of a medium for light that leads to the observed Doppler shift in the frequency of light. This is key to understanding why the mass-energy equivalence principle holds true specifically for light and not for other types of waves that do require a medium.
How does the video address the discrepancy between the energy observed from different reference frames?
-The video addresses the discrepancy by showing that when accounting for the Doppler shift and the time dilation due to special relativity, the energy observed from the moving frame is always higher than that from the rest frame. This leads to the conclusion that the atom must have lost mass in the process of emitting the photons.
What is the final equation derived from the video's explanation?
-The final equation derived from the video's explanation is that the mass lost (Δm) is equal to the energy lost (E) divided by the square of the speed of light (c²), which is expressed as Δm = E / c².
How does the video relate the concept of time dilation to the Doppler effect?
-The video relates time dilation to the Doppler effect by explaining that the frequency of the light emitted by a moving source appears different to a stationary observer due to the time dilation effect of special relativity. This results in a change in the observed energy of the photons, which is a key part of deriving the mass-energy equivalence principle.
What is the significance of the video's approach to explaining E=mc²?
-The significance of the video's approach is that it provides an intuitive and step-by-step explanation of a complex physical concept without relying on advanced mathematical derivations, making it accessible and understandable to a broader audience.
Outlines
🌟 Intuitive Derivation of E=mc²
The paragraph discusses the historic derivation of the mass-energy equivalence formula, E=mc², as initially presented by Einstein in 1905. It begins with a thought experiment involving a radioactive atom emitting two photons, which leads to the conclusion of the constant speed of light being a key factor in the derivation. The narrative then moves to a rocket scenario where Einstein explains the concept of relativity and the Doppler effect, demonstrating how the energy and mass of the atom change from different reference frames. The paragraph emphasizes the step-by-step visualization of the math involved in this famous equation's derivation.
🚀 Doppler Effect and Energy Conservation
This paragraph delves deeper into the implications of the Doppler effect on light and energy conservation. It explains how the Doppler effect causes a change in the observed frequency and energy of photons when the source is in motion. The discussion focuses on the paradox that arises when comparing the energy of the atom from a stationary frame and a moving frame (the rocket). The paragraph highlights Einstein's realization that the discrepancy in energy can only be resolved by acknowledging that the atom loses mass when it emits photons, laying the groundwork for the mass-energy equivalence principle.
🌌 Special Relativity and the Nature of Light
The paragraph explores the subtleties of the Doppler effect and its unique application to light due to its lack of need for a medium. It contrasts the behavior of light with other types of waves, such as sound waves, which require a medium and do not exhibit the same kind of Doppler shift. The explanation highlights that the constancy of the speed of light in all reference frames is crucial for the energy-momentum relationship. The paragraph also emphasizes the significance of this understanding in the development of the E=mc² equation and the broader implications for the theory of special relativity.
📐 Calculating Relativistic Doppler Shifted Frequencies
This paragraph presents a detailed and intuitive approach to calculating the relativistic Doppler shifted frequencies for a moving atom emitting photons. It explains the process of determining the frequency and wavelength of light from both the rest frame and the moving frame, taking into account time dilation and the effects of special relativity. The explanation is methodical, walking through the steps of calculating the blue-shifted and red-shifted photon energies and how these calculations lead to the conclusion that the energy lost by the atom is equal to the mass lost, as predicted by the mass-energy equivalence principle.
🎓 Deriving E=mc² Through Doppler Shifted Energies
The paragraph concludes the script with the climactic derivation of the E=mc² equation through the analysis of Doppler shifted energies of photons. It simplifies the complex mathematical expressions using approximation techniques and binomial expansion, leading to the final equation that relates the lost mass to the energy of the emitted photons. The summary emphasizes the elegance and simplicity of the derivation, offering a profound understanding of the fundamental principles of special relativity and the mass-energy equivalence.
Mindmap
Keywords
💡Einstein
💡Mass-energy equivalence
💡Radioactive atom
💡Photons
💡Constant speed of light
💡Doppler effect
💡Reference frame
💡Momentum
💡Rocket
💡Time dilation
💡Relativistic Doppler effect
Highlights
The video presents an intuitive derivation of E=mc², showcasing Einstein's original method from 1905.
The derivation begins with a thought experiment involving a radioactive atom emitting two photons, illustrating the conservation of momentum.
The video explains how the constant speed of light leads to the concept of mass-energy equivalence through a step-by-step visualization of the necessary math.
A key point is that the atom emits two photons in opposite directions to ensure it remains at rest, highlighting the importance of the atom's initial and final states in the energy calculation.
The video introduces a rocket moving at a constant velocity, with Einstein jumping into it, to explore the energy of the atom from a moving reference frame.
The Doppler effect is introduced as a crucial concept, explaining how it affects the observed frequency and energy of the photons due to the moving atom.
The video emphasizes that the discrepancy in the observed energy of the photons between the stationary and moving frames implies a loss of mass by the atom.
Einstein's thought process is highlighted, showing how he approached the problem without preconceived notions and was open to the possibility that losing energy means losing mass.
The video contrasts the Doppler effect for light with that for sound waves, explaining why the mass-energy equivalence is only observed in the case of light due to its lack of a medium and constant speed in all reference frames.
The derivation continues with a detailed explanation of how to calculate the relativistic Doppler shift for the photons, providing a clear and logical approach to understanding the effect.
The video demonstrates the calculation of the blue-shifted and red-shifted photon energies, leading to the conclusion that the total energy in the moving frame is greater than in the rest frame.
The final step of the derivation is presented, where the equation for the energy lost in the photons is equated to the mass lost, resulting in the famous equation E=mc².
The video emphasizes the importance of special relativity in understanding the mass-energy equivalence and how it emerges naturally from the principles of physics.
The derivation concludes with a summary that ties together the atom's energy loss, photon emission, and mass loss, reinforcing the concept of mass-energy equivalence.
The video's approach to explaining E=mc² is praised for its clarity and intuitive nature, aiming to provide viewers with a deep understanding of the concept.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: