Solving Polynomial and Rational Equations

Stacy Colaiacovo

15 Jan 202436:47

EducationalLearning

32 Likes 10 Comments

TLDRThe video script offers a comprehensive review of solving polynomial and rational equations. It explains that a polynomial equation consists of terms with the form K * x^n, where K is a real number and n is a positive integer. The degree of the polynomial dictates the number of solutions, with linear, quadratic, cubic, and higher degree equations being discussed. The script covers solving strategies such as isolating variables, using inverse operations, and applying the quadratic formula. It also introduces rational equations, which involve fractions with polynomials in the denominator. The importance of considering restrictions on the values of the variable that make the denominator zero is emphasized. Techniques for solving rational equations include cross-multiplication for proportions and using the least common denominator (LCD) to eliminate fractions. The script concludes with a reminder to check solutions against any restrictions to ensure they are valid, and mentions the possibility of extraneous solutions where the only solution obtained is not valid due to restrictions.

Takeaways

📚 An equation is a mathematical statement where two expressions are equal to each other.
🔢 A polynomial equation consists of terms in the form of K * x^n, where K is a real number and n is a positive integer.
📈 The degree of a polynomial equation is the highest exponent on the variable x and dictates the number of solutions the equation has.
🔍 Linear equations (degree 1) have one solution, quadratic equations (degree 2) have two solutions, and so on.
🤔 To solve polynomial equations, use isolation techniques and inverse operations, such as taking the square root for quadratic equations.
🔑 Factoring and the quadratic formula are common strategies for solving quadratic equations, especially when the equation cannot be simplified by isolating x^2.
🚫 When dealing with rational equations, it's crucial to identify and exclude any values of x that would make the denominator zero.
🤓 Rational equations can be solved by cross-multiplication if they represent a proportion or by multiplying through by the least common denominator (LCD).
📉 Rational equations may have no valid solutions if the only solution found is an extraneous solution (a restricted value).
📝 When solving rational equations, always check the solution against the restrictions to ensure it doesn't result in a zero denominator.
📈 The process of solving polynomial and rational equations involves simplifying, factoring, applying algebraic techniques, and checking for extraneous solutions.

Q & A

What is the fundamental form of terms in a polynomial equation?
-The fundamental form of terms in a polynomial equation is K * x to the N power, where K is a real number coefficient and N is a positive integer exponent.
What is the name given to a polynomial equation with a degree of one?
-A polynomial equation with a degree of one is called a linear polynomial or a linear equation.
How many solutions does a quadratic equation have?
-A quadratic equation, which has a degree of two, should have two solutions.
What is the process called when you isolate the variable x by itself in an equation?
-The process is called isolating the variable or isolating x, and it involves using inverse operations to get the variable x alone on one side of the equation.
What is the term for an equation that contains a fraction of polynomials?
-An equation that contains a fraction of polynomials is called a rational equation.
What is the main restriction when solving rational equations?
-The main restriction when solving rational equations is that the denominator cannot be equal to zero, as this would make the fraction undefined.
How can you identify if a rational equation is a proportion?
-A rational equation is a proportion if there is one term on both sides of the equal sign, indicating that one fraction is equal to another fraction.
What is the method used to solve a proportion?
-The method used to solve a proportion is cross-multiplication, which involves multiplying the numerator of one fraction by the denominator of the other, and vice versa, and then checking if the cross products are equal.
What is the term for a solution that results from solving an equation but is not valid due to restrictions?
-The term for such a solution is an extraneous solution.
What is the least common denominator (LCD) used for in the context of rational equations?
-The least common denominator (LCD) is used to eliminate fractions in a rational equation by multiplying every term by the LCD, which converts the equation into a polynomial equation that is easier to solve.
How can you check the validity of a solution obtained from solving an equation?
-You can check the validity of a solution by plugging it back into the original equation. If the equation holds true with the given solution, it is considered valid. If it results in a denominator of zero, the solution is not valid.
What is the preferred form for expressing the solutions of polynomial equations?
-The preferred form for expressing the solutions of polynomial equations is as reduced fractions rather than decimals, as fractions are more precise and do not require rounding.

Outlines

00:00

📚 Introduction to Polynomial and Rational Equations

The video begins with an introduction to solving polynomial and rational equations. It explains what constitutes a polynomial equation, characterized by terms in the form of K * x^N, where K is a real number and N is a positive integer. The importance of the degree of the polynomial is emphasized as it determines the number of solutions the equation will have. The video outlines different types of polynomial equations: linear, quadratic, cubic, and so on, and mentions solving strategies such as isolating variables and using inverse operations. It also states the focus will be on quadratic equations, but linear equations will be reviewed as well.

05:01

🔍 Techniques for Solving Quadratic Equations

This paragraph delves into solving quadratic equations, which are polynomial equations of degree two. It discusses various methods to address these equations, including isolating the squared term, factoring, and using the quadratic formula. The process of taking the square root of both sides is covered, along with the necessity of considering both positive and negative roots. The paragraph also touches on solving equations with irrational solutions and the preference for exact fractional solutions over decimal approximations.

10:04

📝 Factoring and Quadratic Formula Application

The speaker discusses the application of factoring and the quadratic formula in solving quadratic equations. It highlights that factoring is a preferred method when possible, but the quadratic formula is a reliable alternative. The paragraph includes a step-by-step demonstration of factoring quadratic expressions and finding the solutions that make each factor equal to zero. It also addresses the use of the quadratic formula, emphasizing the importance of correctly identifying and substituting the coefficients (a, b, and c) into the formula.

15:06

🚫 Addressing Non-Factorable Quadratic Equations

This section addresses quadratic equations that cannot be factored. It explains that if factoring is not possible, the quadratic formula must be used. The paragraph provides a detailed example of applying the quadratic formula, including the process of simplifying the radical and cautioning against improper division into the radical. It also explains how to handle the results of the quadratic formula, emphasizing the need to simplify and check for extraneous solutions.

20:06

🌐 Overview of Rational Equations and Their Solutions

The video moves on to rational equations, which are equations containing fractions with polynomials in the numerator and/or the denominator. It stresses the importance of recognizing that the denominator cannot be zero and that any value of x that makes the denominator zero must be restricted. The paragraph outlines two types of rational equations: proportions (where cross-multiplication can be used) and non-proportional rational equations (which may require finding a common denominator or other algebraic manipulations to solve).

25:07

🧐 Solving Proportions and Rational Equations with Restrictions

This paragraph focuses on solving proportions and rational equations, including how to identify and handle restricted values. It provides examples of cross-multiplying to solve proportions and using the least common denominator (LCD) to clear fractions in non-proportional rational equations. The importance of checking the validity of the solution against the restrictions is emphasized, and the concept of extraneous solutions is introduced.

30:09

🔗 Multiplication by LCD to Clear Fractions

The speaker demonstrates the technique of multiplying every term in a rational equation by the LCD to eliminate fractions, turning the equation into a simpler polynomial equation that can be solved more easily. The paragraph shows step-by-step multiplication by the LCD, factoring out common terms, and solving the resulting linear equation. It also reminds viewers to consider the restrictions throughout the process and to verify that the obtained solution does not violate any of them.

35:10

🚷 Identifying and Handling Extraneous Solutions

The final paragraph discusses the concept of extraneous solutions in rational equations. It clarifies that if the only solution obtained for a rational equation is one that is restricted (i.e., it makes a denominator zero), then the equation has no valid solution. The importance of checking solutions against restrictions is reiterated, and the video concludes with an invitation for viewers to ask questions and an assurance that the covered material will be reviewed in more detail later in the course.

Mindmap

Keywords

💡Polynomial Equation

A polynomial equation is a mathematical statement where the sum of the terms, each consisting of a variable raised to a non-negative integer power and multiplied by a coefficient, is equal to zero. In the video, the instructor explains that polynomial equations can take various forms but are characterized by terms like K * x^N, where K is a real number and N is a positive integer. The degree of the polynomial dictates the number of solutions it has, with linear, quadratic, cubic, and quartic being common classifications based on the highest power of the variable.

💡Degree of a Polynomial

The degree of a polynomial is the highest power of the variable in the polynomial equation. It is a key determinant of the number of solutions the equation will have. For instance, a linear polynomial (degree 1) has one solution, a quadratic (degree 2) has two solutions, and so on. In the script, the degree is used to classify polynomials and to anticipate the number of solutions that will be sought during the solving process.

💡Quadratic Equation

A quadratic equation is a specific type of polynomial equation with a degree of two. It is of the form ax^2 + bx + c = 0, where a, b, and c are constants and a ≠ 0. The video focuses on solving quadratic equations, which can be done using various methods such as factoring, completing the square, or applying the quadratic formula. Quadratic equations are important in many areas of mathematics and have two solutions, which can be real or complex numbers.

💡Rational Equation

A rational equation is an equation that contains at least one fraction with a variable in the denominator. These equations require special consideration because the variable cannot take on values that would make the denominator equal to zero. In the video, the instructor discusses how to solve rational equations by either transforming them into a proportion (if there is only one term on both sides) or by using the least common denominator to eliminate the fractions.

💡Least Common Denominator (LCD)

The least common denominator is the smallest multiple that each of the denominators of a set of fractions can divide into. When solving rational equations, the LCD is used to multiply both sides of the equation to eliminate fractions, converting the equation into a polynomial form that is easier to solve. The video script illustrates the process of finding the LCD and using it to simplify rational equations.

💡Extraneous Solution

An extraneous solution is a value that may solve the algebraic manipulation of a rational equation but is not a valid solution to the original equation because it would make the denominator of one of the fractions equal to zero. In the context of the video, the instructor emphasizes the importance of checking that the solutions obtained for rational equations do not include any restricted values, which are the values that would result in division by zero.

💡Factoring

Factoring is a mathematical method of breaking down a polynomial into a product of its factors. It is a common technique used to solve polynomial equations, especially quadratic equations. In the video, the instructor demonstrates how to factor quadratic equations to find their solutions and also mentions that factoring can be applied to higher degree polynomials if possible.

💡Quadratic Formula

The quadratic formula is a standard algebraic method used to find the solutions for any quadratic equation. The formula is x = (-b ± √(b² - 4ac)) / (2a), where a, b, and c are coefficients from the quadratic equation ax² + bx + c = 0. The video script includes the use of the quadratic formula as one of the methods to solve quadratic equations when factoring is not possible.

💡Cross-Multiplication

Cross-multiplication is a technique used to solve proportions or equations that can be written in the form of a proportion (a single fraction equals a single fraction). By multiplying the numerator of one fraction by the denominator of the other, and vice versa, and setting the products equal to each other, one can solve for the variable. The video demonstrates the use of cross-multiplication in solving rational equations that are proportions.

💡Linear Equation

A linear equation is a polynomial equation of the first degree, meaning it has a degree of one. It is of the form ax + b = 0, where a and b are constants and x is the variable. In the video, the instructor explains how to solve linear equations, which typically involves isolating the variable x to find its value. Linear equations have a single solution.

💡Inverse Operations

Inverse operations are mathematical procedures that 'reverse' a given operation. For example, the inverse of multiplication is division, and the inverse of addition is subtraction. In the context of solving equations, inverse operations are used to isolate the variable. The video script describes using inverse operations to solve both linear and quadratic equations by reversing the operations that were used to form the equation.

Highlights

A polynomial equation is defined by its terms being in the form of K * x to the N power, where K is a real number and N is a positive integer.

Polynomial equations can be categorized by their degree, which dictates the number of solutions (linear, quadratic, cubic, etc.).

Linear equations with a degree of one have a single solution and are solved by isolating x to the first power.

Quadratic equations with a degree of two have two solutions and can be solved using various techniques, including factoring and the quadratic formula.

To solve polynomial equations, one can use isolation techniques and inverse operations, such as taking the square root for a quadratic.

Rational equations involve fractions with polynomials in the numerator and/or the denominator.

Solving rational equations requires identifying and restricting values of x that would make any denominator zero.

Proportions, a type of rational equation, can be solved using cross-multiplication.

When solving rational equations, it's essential to check for extraneous solutions that result from restricted values.

The least common denominator (LCD) method can be used to eliminate fractions in rational equations by multiplying both sides by the LCD.

When using the quadratic formula, it's crucial to identify the coefficients a, b, and c correctly and follow the formula accurately.

Factoring is a preferred method for solving quadratic equations when possible, as it can be simpler than using the quadratic formula.

If factoring is not possible, the quadratic formula provides a consistent method to find the solutions to any quadratic equation.

Solutions to polynomial equations can be real, complex, or a combination, depending on the nature of the equation.

When taking the square root during the solution process, a plus or minus sign should be included to account for both possible values.

Rational equations can sometimes be simplified to a proportion by ensuring there is only one term on each side of the equation.

It's important to simplify radicals to their simplest form when presenting the final solutions to an equation.

Checking solutions by plugging them back into the original equation can validate the correctness of the solution.

Fractions are often preferred over decimals in solutions for their precision and to avoid rounding errors.

Transcripts

Browse More Related Video

Solving Higher-Degree Polynomials by Synthetic Division and the Rational Roots Test

Solving Polynomial Equations By Factoring and Using Synthetic Division

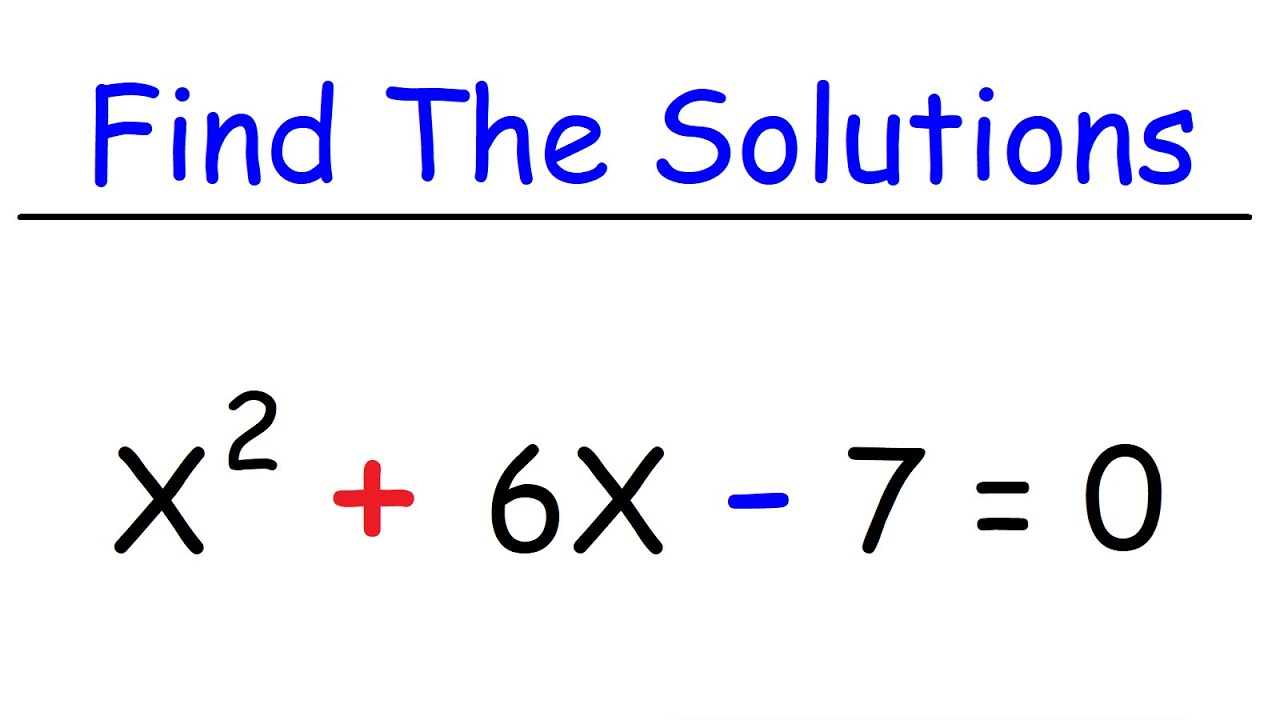
How To Find The Real & Imaginary Solutions of Polynomial Equations

Solving Polynomial Inequalities

Finding All Zeros of a Polynomial Function Using The Rational Zero Theorem

Ch. 1.5 Equations

Related Tags

Polynomial Equations Rational Equations Quadratic Solving Linear Algebra Mathematical Review Educational Content Inverse Operations Factoring Techniques Quadratic Formula Cross Multiplication Algebraic Strategies