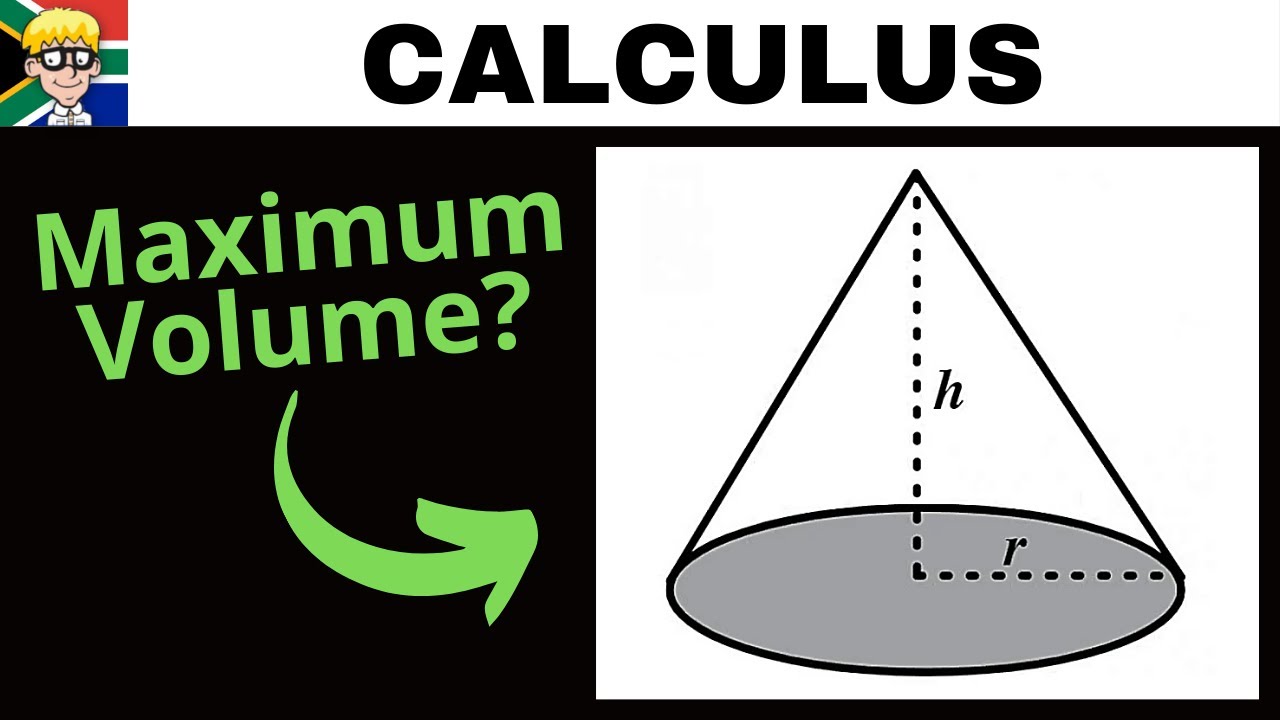
Find the Volume of Any Shape Using Calculus
TLDRThis educational video script demonstrates how to use calculus to derive the volumes of various geometric shapes, such as a cone, which is not as straightforward as calculating the volume of a cylinder. The presenter guides viewers through the process of approximating the volume of a cone with a series of disks (cylinders), and then refines the approximation by shrinking the height of these disks to an infinitesimal scale. The key steps involve setting up a sum of the volumes of these disks, expressing the sum in terms of height, and performing the integration. The script challenges viewers to find the relationship between the radius and height of the cone and provides a detailed walkthrough of the mathematical derivation. The video aims to illustrate the practical applications of calculus and inspire viewers to explore the derivation of other shapes, such as spheres or pyramids.
Takeaways
- 📚 The video teaches how to use calculus to derive the volume of different shapes, starting with a cone as an example.
- 📐 The volume of a cylinder is given by the formula base area (πr²) times height, which is a simpler shape to understand.
- 🍦 The volume of a cone is approximated using a series of disks (cylinders), each with a height ΔH and a radius R.
- 🔍 Calculus is applied by shrinking ΔH to an infinitely small size, leading to an infinite number of disks, which makes the approximation exact.
- 🧩 The process involves setting up a sum of the volumes of these disks, expressing the sum in terms of height, and then integrating.
- 🤔 The video challenges viewers to find the relationship between the radius R and the height H of the cone, hinting at an inverse relationship.
- 📉 The relationship between R and H is derived as R = (H - h) / H, which simplifies the expression for the radius in terms of height.
- 📈 The volume of the cone is expressed as an integral from 0 to H with the formula πR²/H² * h²dH.
- ✅ The final integration yields the volume of the cone as (1/3)πR²H, which matches the expected formula for a cone's volume.
- 🎯 The video encourages viewers to apply the same calculus procedure to other shapes, such as spheres or pyramids, to derive their volumes.
- 🎓 The presenter finds the process of deriving formulas using calculus satisfying and hopes the viewers will too, emphasizing the practical application of calculus.
Q & A
What is the main topic of the video?
-The main topic of the video is how to use calculus to derive the volumes of different shapes such as a cone, pyramid, or sphere.
Why might someone struggle to give the volume of a cone off the top of their head?
-Someone might struggle because the formula for the volume of a cone is not as straightforward as that of a cylinder, which is simply the base area times height.
What is the volume formula for a cylinder?
-The volume formula for a cylinder is the base area, which is πR² (pi times the radius squared), times the height.
How does the video suggest approximating the volume of a cone?
-The video suggests approximating the volume of a cone by using a series of disks (cylinders) stacked along the height of the cone.
What does calculus allow us to do with the approximation of the cone's volume?
-Calculus allows us to shrink the height of each disk (ΔH) to be infinitely small, which means we have infinitely many disks, and this makes our approximation exact.
What is the expression for the volume of a cone that the video aims to derive?
-The video aims to derive the expression for the volume of a cone, which is one-third πR²H (pi times the radius squared times the height).
What are the three steps outlined in the video for deriving the volume of a cone?
-The three steps are: 1) Set up a sum by approximating the volume with disks, 2) Express the sum in terms of the height, and 3) Perform the integration.
How does the video suggest finding the relationship between the radius (R) and height (H) of the cone?
-The video suggests finding the relationship by considering the cone's geometry and the fact that at half the height, you have half the radius, indicating an inverse relationship.
What is the integral formula used in the video to derive the volume of the cone?
-The integral formula used is V = πR²∫(R²/H²)dH from 0 to H, which simplifies to V = (1/3)πR²H³ after integration.
How does the video conclude the final volume of the cone?
-The video concludes that the final volume of the cone is (1/3)πR²H, which matches the expected formula for the volume of a cone.
What is the significance of the video's approach to teaching calculus?
-The significance is that it demonstrates a practical application of calculus, allowing viewers to derive formulas for themselves rather than just accepting them, thus enhancing understanding and appreciation for calculus.
Outlines
📚 Deriving Volumes Using Calculus
The video script introduces the challenge of calculating the volume of various geometric shapes without relying on memorized formulas. It proposes the use of calculus to derive the volume of a cone as an example, which can be extended to other shapes like pyramids and spheres. The process involves approximating the volume of a cone with a series of disks (cylinders), each with a height 'Delta H' and a base area of 'PI R squared'. The script suggests starting with an intuitive guess for the cone's volume, which is later refined using calculus to shrink 'Delta H' to an infinitesimal size, leading to an exact volume calculation. The video outlines a three-step procedure: setting up a sum, expressing the sum in terms of height, and performing the integration.
🔍 Establishing the Relationship Between Radius and Height
This paragraph delves into the task of finding the relationship between the radius 'R' and the height 'H' of the cone. It provides a hint that at 25% of the height, one is 75% of the way up the radius, and vice versa, indicating an inverse relationship. The narrator guides the viewer through a thought experiment, simplifying the problem by setting the radius and height to 1 unit each, to establish a direct proportion. The challenge is to express 'R' in terms of 'H', which is crucial for the integration process. The paragraph discusses potential pitfalls in algebraic manipulation and suggests a more natural way to express the relationship, simplifying the substitution into the volume formula and preparing for the integration step.
📈 Calculating the Volume with Integration
The final paragraph focuses on the integration step to calculate the exact volume of the cone. It starts by transforming the sum of the volumes of the disks into an integral, as 'Delta H' approaches infinity, making the approximation exact. The integral is set up with the limits from 0 to 'Big H', the height of the cone. The script explains the integration process for 'H squared', highlighting the importance of raising the power and dividing by the corresponding factor. The integration results in a formula that, when simplified, yields the volume of the cone as '(1/3) PI R squared H', confirming the initial intuitive guess but with a more rigorous derivation. The video concludes by encouraging viewers to apply this method to other shapes and to explore the value of calculus in deriving equations for themselves.
Mindmap
Keywords
💡Volume
💡Cylinder
💡Cone
💡Calculus
💡Integration
💡Radius
💡Height
💡Disk
💡Sum
💡Approximation
Highlights
The video demonstrates how to use calculus to derive the volumes of various shapes, starting with a cone as an example.
Calculus is used to approximate the volume of a cone using a series of disks, which are simplified cylinders.
The base area of each disk is calculated using the formula PI * R^2, where R is the radius.
As Delta H (the height of each disk) approaches infinity, the approximation becomes exact, revealing the true volume of the cone.
The volume of the enclosing cylinder is given as PI * R^2 * H, providing a basis for comparison with the cone's volume.
The actual volume of a cone is derived to be one third of the volume of the enclosing cylinder: (1/3) * PI * R^2 * H.
The process involves setting up a sum of the volumes of the disks and expressing this sum in terms of height.
The relationship between the radius R and height H of the cone needs to be established for the integration process.
A hint is provided that relates the percentage of height to the percentage of radius in the cone.
The challenge is to find an expression that relates the variable radius R to the height H.
An example is given to illustrate the inverse relationship between height and radius in the cone.
The expression R = (H - h) / H * R is derived to represent the relationship between radius and height.
A simpler expression R = H / H * h is introduced to avoid complex algebra during integration.
The volume of the cone is then expressed in terms of height using the derived relationship between R and H.
Integration is performed to calculate the exact volume of the cone, turning the sum into an integral.
The integral calculation simplifies to V = (1/3) * PI * R^2 * H, confirming the earlier derived formula for the cone's volume.
The video concludes by emphasizing the value of calculus in deriving equations and understanding the derivation process.
The method demonstrated can be applied to other shapes such as spheres or pyramids to derive their volumes.
The presenter encourages viewers to try deriving the volume of a sphere or pyramid as a next step.
The video ends with an announcement about new posters available on the presenter's store.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: