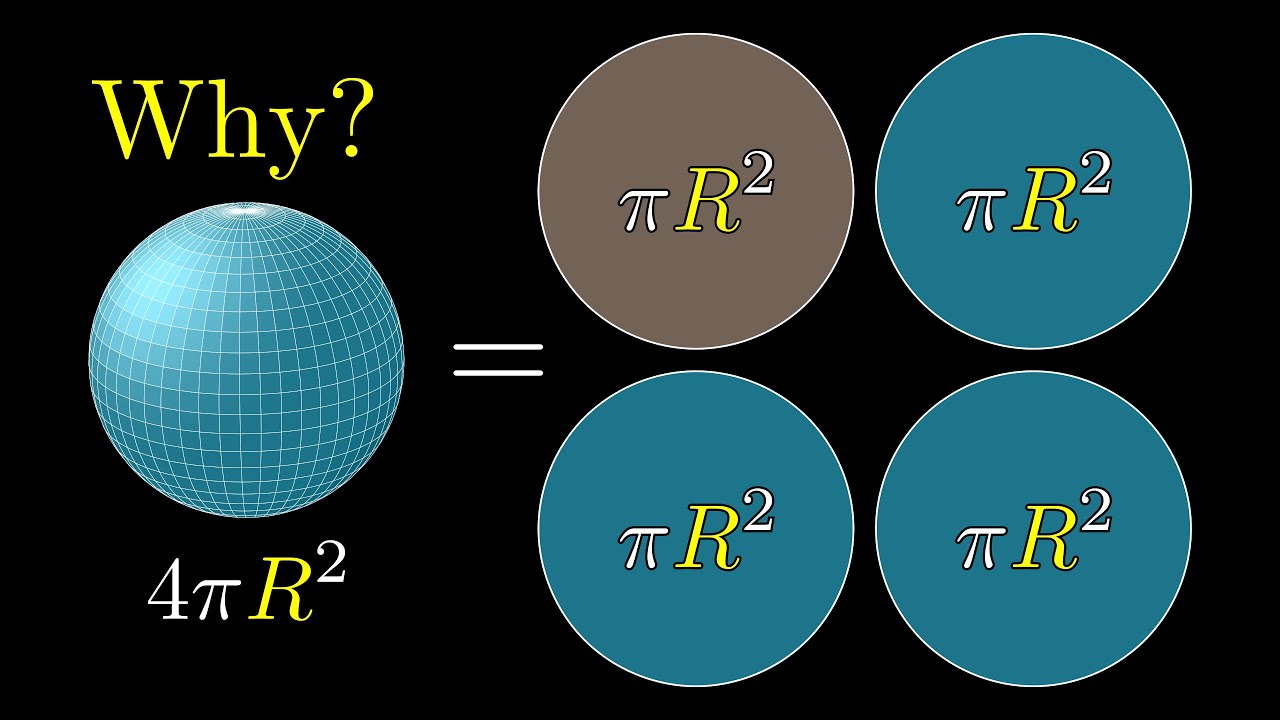Understanding the Volume of a Sphere Formula [Using High School Geometry]
TLDRThe formula for the volume of a sphere, 4/3 πr³, is derived by dividing the sphere into numerous pyramids with square bases. The height of each pyramid equals the sphere's radius. By summing the volumes of these pyramids, factoring out common elements, and recognizing that the sum of the bases equates to the sphere's surface area (4πr²), the formula simplifies to 4/3 πr³. This video explains the step-by-step geometric and algebraic process behind this derivation.
Takeaways
- 📚 The formula for the volume of a sphere is derived from dividing the sphere into equal-sized pyramids with square bases.
- 📐 Each pyramid's volume is calculated using the formula \( \frac{1}{3} \times \text{base area} \times \text{height} \).
- 🔍 The height of all pyramids is shown to be equal to the sphere's radius, simplifying the volume calculation.
- 📈 The equation for the volume of a single pyramid is simplified to \( \frac{r}{3} \times B \), where \( B \) is the base area.
- 🔢 The volume of the entire sphere is the sum of the volumes of all individual pyramids.
- 🌐 The process involves adding up the volumes of pyramids from base-1 to base-n, representing the last pyramid.
- 🧩 Algebra is used to factor out common terms, resulting in \( \frac{r}{3} \times \sum \text{of all bases} \).
- 🌀 The sum of all bases equates to the sphere's surface area, which is \( 4\pi r^2 \).
- 📉 The surface area of the sphere is four times the area of the circle with the same radius, each being \( \pi r^2 \).
- 🔄 The final formula for the volume of the sphere is obtained by substituting the sum of the bases with the surface area, resulting in \( \frac{4}{3}\pi r^3 \).
- 🌍 The formula \( \frac{4}{3}\pi r^3 \) is applicable to find the volume of any sphere regardless of its size.
Q & A
What is the formula for the volume of a sphere?
-The formula for the volume of a sphere is \( \frac{4}{3} \pi r^3 \), where \( r \) is the radius of the sphere.
How is the volume of a sphere derived using the concept of pyramids?
-The volume of a sphere is derived by imagining the sphere as being composed of many small pyramids with square bases. The volume of each pyramid is calculated and then summed up to find the total volume of the sphere.
What is the formula for the volume of a pyramid with a square base?
-The volume of a pyramid with a square base is given by \( \frac{1}{3} \times \text{base area} \times \text{height} \).
Why is the height of the pyramids in the sphere equal to the radius of the sphere?
-The height of the pyramids is equal to the radius because when the sphere is divided into pyramids with square bases, each pyramid's apex touches the center of the sphere, making its height equal to the sphere's radius.
How is the sum of the areas of the bases of the pyramids related to the surface area of the sphere?
-The sum of the areas of the bases of the pyramids forms the surface area of the sphere, which is \( 4\pi r^2 \).
What is the formula for the surface area of a sphere?
-The formula for the surface area of a sphere is \( 4\pi r^2 \).
Why is the surface area of a sphere four times the area of its largest circle (great circle)?
-The surface area of a sphere is four times the area of its great circle because the sphere can be conceptualized as being composed of four identical circular segments, each with an area of \( \pi r^2 \).
How does the script simplify the equation for the volume of the sphere?
-The script simplifies the equation by factoring out \( \frac{1}{3} \) and the radius \( r \), resulting in \( \frac{r}{3} \times \text{sum of all base areas} \), and then replacing the sum of all base areas with the surface area formula.
What is the significance of the number 4 in the surface area formula for a sphere?
-The number 4 in the surface area formula \( 4\pi r^2 \) signifies that the surface area of a sphere is four times the area of one of its great circles.
How does the script conclude the final formula for the volume of a sphere?
-The script concludes the final formula by combining the factored terms and the surface area formula, rearranging to get \( \frac{4}{3} \pi r^3 \).
What is the practical application of knowing the volume of a sphere?
-Knowing the volume of a sphere is useful in various fields such as physics, engineering, and architecture, where calculations involving the space occupied by spherical objects are necessary.
Outlines
📚 Deriving the Sphere Volume Formula
This paragraph explains the derivation of the formula for the volume of a sphere. It begins by visualizing a perfect sphere and dividing it into pyramids with square bases. The volume of each pyramid is calculated using the formula (1/3) * base area * height, with the height being equal to the sphere's radius (r). The process simplifies to summing the volumes of all pyramids, represented as a series from base-1 to base-n. The formula is then simplified by factoring out (1/3) and r, leading to the expression r/3 * sum of all bases. The paragraph concludes by identifying the sum of all bases as the surface area of the sphere, which is 4πr², and substituting this into the formula to arrive at the final volume formula: (4/3)πr³.
Mindmap
Keywords
💡Volume
💡Sphere
💡Pyramids
💡Base
💡Height
💡Radius
💡Surface Area
💡Circumference
💡Algebra
💡Factoring
💡Summation
Highlights
The derivation of the volume of a sphere formula is explained using a geometric approach.
A perfect sphere is visualized and its volume filled for the demonstration.
The sphere is divided into equal-sized pyramids with square bases for volume calculation.
Each pyramid's volume is calculated using the formula one-third base area times height.
A proof is provided that all pyramids' heights are equal to the sphere's radius.
The volume equation simplifies to one-third times base area times radius.
The base area is replaced with 'B' and the radius with 'r' for the equation.
The volume of the sphere is found by summing the volumes of individual pyramids.
A formula is presented for the sum of the volumes of all pyramids.
Algebra is used to factor out constants from the volume formula.
The sum of all pyramid bases is identified as the sphere's surface area.
The surface area of a sphere is explained to be four times the area of a great circle.
The formula for the surface area, four pi r squared, is derived.
The sum of bases in the volume formula is replaced with the surface area formula.
The final volume formula, four-thirds pi r cubed, is obtained by rearranging terms.
The formula is applicable to spheres of any size.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: