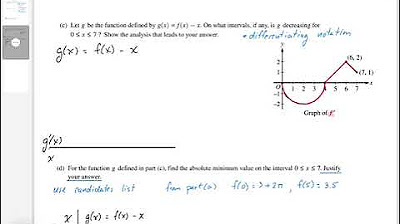2019 AP Calculus AB & BC Free Response Question #3

Tom Cochran Life is a PiWay
16 May 201913:39
EducationalLearning
32 Likes 10 Comments

TLDRThe video script is a detailed walkthrough of a complex calculus problem from the 2019 AP Calculus AB exam. It involves understanding the graph of a function, calculating definite integrals, and applying the fundamental theorem of calculus. The presenter breaks down the problem into parts, explaining how to find the value of a definite integral given the integral from -6 to 5 equals 7. They then evaluate the integral from -2 to 5, using the graph to determine areas and applying properties of integrals. The solution involves calculating areas of triangles and a quarter circle, and subtracting these from 7 to find the integral's value. The video also covers evaluating a new function G, defined as an integral from -2 to X, and finding its absolute maximum value on the interval -2 to 5. The presenter uses the extreme value theorem and the derivative of G to find critical points and evaluate G at specific x-values to determine the maximum. Finally, the script touches on evaluating a limit as x approaches 1, involving finding the slope of the graph at x=1 and simplifying the expression using trigonometric identities. The presenter emphasizes the importance of understanding the problem's requirements and not over-simplifying when not necessary, especially in the context of an AP exam.

Takeaways
  • ๐Ÿ“ˆ The problem involves a graph with a quarter circle centered at (5,3) and a line segment, where the definite integral from -6 to 5 equals 7.
  • ๐Ÿ” The definite integral from -6 to 2 plus the integral from -2 to 5 equals the total signed area under consideration, which is given as 7.
  • โœ‚๏ธ By breaking down the integral into separate parts, the problem becomes more manageable, highlighting the properties of definite integrals.
  • ๐Ÿ“ The area of various geometric shapes (triangles, quarter circle) above and below the x-axis are calculated with consideration of their signs.
  • ๐Ÿงฎ The value of the integral is found by subtracting a calculated area from 7, resulting in an expression involving ฯ€.
  • ๐Ÿ”‘ The antiderivative of 4 is 4x, and by applying the fundamental theorem of calculus, the value of the definite integral can be found without simplifying further.
  • ๐Ÿ“‰ For the function G, defined as an integral from -2 to x, the absolute maximum value on the interval [-2, 5] is sought, leveraging the extreme value theorem.
  • ๐Ÿ” The derivative of G, G'(x), is found to be equal to f(x), which helps in identifying critical points where G'(x) equals zero.
  • ๐Ÿ“Œ Endpoints and critical points of the interval are evaluated to determine the maximum value of G, which is found to be at G(5).
  • ๐ŸŽ“ On the AP exam, it's important to follow the instructions regarding the level of simplification required for the answers.
  • โฒ๏ธ Time management is crucial; avoid over-simplification unless explicitly asked for, as it may risk losing points due to time wasted.
Q & A

  • What is the main topic of the transcript?

    -The main topic of the transcript is a detailed explanation and solution process for a calculus problem from the 2019 AP Calculus AB exam.

  • What is the significance of the graph provided in the problem?

    -The graph is significant because it represents a combination of a line segment and a quarter circle, which are used to calculate areas and integrals as part of the problem.

  • What is the value of the definite integral from negative 6 to 5 mentioned in the transcript?

    -The value of the definite integral from negative 6 to 5 is given as 7.

  • What is the strategy used to find the value of the integral from negative 6 to 2?

    -The strategy involves breaking down the integral into parts, recognizing it as a portion of the entire signed area represented by the integral from negative 6 to 5, and then using properties of definite integrals to find the value.

  • How is the area between the function f(x) and the x-axis calculated in the problem?

    -The area is calculated by breaking it down into simpler shapes like triangles and a quarter circle, calculating the area of each shape with appropriate signs based on their position relative to the x-axis, and then summing these areas.

  • What is the antiderivative of the function 4 in the context of the problem?

    -The antiderivative of the function 4 is 4x, as the antiderivative of a constant is the constant times the variable.

  • How does the Fundamental Theorem of Calculus apply to finding the value of the definite integral?

    -The Fundamental Theorem of Calculus states that the definite integral of a function can be found by evaluating the antiderivative of the function at the upper and lower limits of integration and taking the difference.

  • What is the new function G defined in Part B of the problem?

    -Function G is defined as a definite integral from negative 2 to x, where x is the upper limit of integration, making G dependent on the variable x.

  • What theorem is used to justify finding the absolute maximum value of G on the interval negative 2 to 5?

    -The Extreme Value Theorem is used, which states that a continuous function on a closed interval is guaranteed to have both a maximum and a minimum value.

  • How is the derivative of G found in the problem?

    -The derivative of G is found by applying the fundamental theorem of calculus, which involves copying the integrand and replacing the integration variable with the upper limit of integration.

  • What is the approach to evaluate the limit given in the problem?

    -The approach is to substitute the value that x is approaching into the limit expression and simplify the expression to find the limit.

Outlines
00:00
๐Ÿ“Š Calculus Problem Solving with Definite Integrals

This paragraph discusses a problem from the 2019 AP Calculus exam involving a graph with a quarter circle and a line segment. The task is to calculate the value of a definite integral using the given information that the integral from negative 6 to 5 equals 7. The speaker breaks down the integral into parts, uses properties of definite integrals to find the value, and applies the concept of signed area. The solution involves calculating areas of triangles and a quarter circle, and uses the graph to find function values, leading to an integral value of negative four plus nine PI by four.

05:01
๐Ÿ” Evaluating Antiderivatives and Critical Points

The second paragraph focuses on evaluating an antiderivative to find the value of a definite integral. The antiderivative of 4x is calculated, and the fundamental theorem of calculus is applied to find the difference between the function values at given points. The paragraph also introduces a new function G, defined as a definite integral involving the function F. The task is to find the absolute maximum value of G on a given interval. The extreme value theorem is mentioned, and the derivative of G is found using the fundamental theorem of calculus. The values of G at critical points and endpoints are calculated to determine the maximum value.

10:02
๐ŸŽ“ AP Exam Strategies and Limit Evaluation

The final paragraph discusses strategies for approaching limits in the context of the AP exam. It provides a step-by-step method for evaluating a limit by substituting the value that x approaches. The paragraph also covers finding the derivative of a function, calculating slopes from a graph, and simplifying expressions involving arctangent to numerical values. The use of the unit circle and trigonometric identities to simplify the expression is explained. The speaker advises on when to stop simplifying based on AP exam grading standards and teacher instructions.

Mindmap
Keywords
๐Ÿ’กDefinite Integral
A definite integral is a fundamental concept in calculus that represents the signed area under a curve between two points on the x-axis. In the video, it is used to find the area between the graph of a function and the x-axis over a specified interval. The script describes how to calculate this by breaking it into parts and using the properties of integrals, such as the integral from negative 6 to 5 being the sum of integrals from negative 6 to negative 2 and from negative 2 to 5.
๐Ÿ’กGraph
A graph in the context of the video is a visual representation of a function, showing how y values (dependent variable) relate to x values (independent variable). The video discusses a specific graph that includes a line segment and a quarter circle, which are used to solve the calculus problems presented.
๐Ÿ’กOrdered Pair
An ordered pair is a set of two numbers, typically written as (x, y), representing a point on a graph. In the script, the ordered pair (3, 3 - โˆš5) is mentioned as being on the graph of the function, which is a key piece of information for solving the integrals.
๐Ÿ’กSigned Area
Signed area refers to the calculation of the area under a curve, taking into account whether the curve is above or below the x-axis. Positive areas are above the x-axis, and negative areas are below it. The video script discusses how to calculate the signed area of various sections of the graph to find the value of a definite integral.
๐Ÿ’กAntiderivative
An antiderivative is a function whose derivative is equal to the original function. In the video, the antiderivative is used to evaluate the definite integral from negative 2 to 5 by applying the fundamental theorem of calculus, which states that the definite integral of a function can be found by evaluating its antiderivative at the endpoints of the interval and taking the difference.
๐Ÿ’กFundamental Theorem of Calculus
The fundamental theorem of calculus is a theorem that links the concept of the definite integral to that of the antiderivative. The video demonstrates its use in evaluating definite integrals by finding antiderivatives and applying the theorem to calculate the area under the curve over a given interval.
๐Ÿ’กContinuous Function
A continuous function is a function that has no breaks or gaps in its graph. In the video, it is mentioned that because the function F is continuous, its integral G is also continuous on the interval from negative 2 to 5, which allows the application of the extreme value theorem.
๐Ÿ’กExtreme Value Theorem
The extreme value theorem states that any continuous function on a closed interval attains both a maximum and a minimum value. In the video, this theorem is used to justify the search for the absolute maximum value of the function G on the interval from negative 2 to 5.
๐Ÿ’กDerivative
The derivative of a function measures the rate of change of the function's output with respect to its input. In the video, the derivative of the function G is found by applying the fundamental theorem of calculus, which is then used to determine where G has critical points, which are potential locations for maximum or minimum values.
๐Ÿ’กLimit
In calculus, a limit is the value that a function or sequence approaches as the input approaches a certain point. The video discusses evaluating a limit by substituting the value that x approaches into the function, which in this case involves the function F and its derivative at a specific point.
๐Ÿ’กArctangent
The arctangent, often denoted as arctan or tan^(-1), is the inverse function of the tangent, giving the angle whose tangent is a given real number. In the video, the arctangent of 1 is discussed, which is related to the tangent of 45 degrees or ฯ€/4 radians, and is used to simplify an expression in the context of evaluating a limit.
Highlights

The problem involves a graph with a quarter circle centered at (5,3) and a line segment.

The ordered pair (3, 3 - โˆš5) is given to be on the graph.

The definite integral from -6 to 5 is given to equal 7, which helps in finding the value of another integral.

The integral from -6 to 5 can be broken down into two parts to find the required integral from -6 to -2.

The definite integral from -2 to 5 corresponds to the area between the graph of f(x) and the x-axis.

Areas of triangles above and below the x-axis are calculated with consideration of their signs.

The area involving the quarter circle requires subtracting the area of the circle from a square to find the signed area.

The value of the integral is found by subtracting a calculated area from 7, resulting in an expression involving ฯ€.

The antiderivative of 4 is 4x, and it's evaluated at the bounds to find a part of the integral's value.

The Fundamental Theorem of Calculus is used to evaluate the definite integral in terms of the function f.

The value of f at specific points is determined from the graph to evaluate the integral.

A new function G is introduced, defined as a definite integral from -2 to x.

The absolute maximum value of G on the interval [-2, 5] is sought, with justification using the Extreme Value Theorem.

The derivative of G is found using the fundamental theorem of calculus by copying the integrand and replacing the parameter.

G' is analyzed for critical points where it equals zero, which correspond to x values of -1 and 1/2.

Values of G at specific points are calculated to determine the maximum value on the interval.

The maximum value of G is identified as G(5), which is a significant outcome of the integral calculations.

A limit evaluation involves replacing x with the value it approaches and simplifying the expression.

The slope of the graph at x=1 is used to find the derivative, which is a key step in evaluating the limit.

The arctangent function is simplified by using the tangent of both sides of an equation, avoiding the need for an exact value.

Transcripts

Browse More Related Video

2022 AP Calculus AB BC Free Response #3

AP CALCULUS AB 2022 Exam Full Solution FRQ#3(c,d)

Definite Integrals!

2023 AP Calculus AB FRQ #5

2022 AP Calculus AB & AP Calculus BC Exam FRQ #3

2011 AP Calculus AB Free Response #4

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
AP CalculusExam ProblemIntegral CalculationGraph AnalysisMath EducationCollege BoardDefinite IntegralsAntiderivativeSigned AreaExtreme ValueFundamental TheoremLimit Evaluation