Distance Versus Displacement
TLDRThe video script explains the fundamental difference between distance and displacement. Distance is a scalar quantity, representing the total ground covered by an object, while displacement is a vector quantity that includes both magnitude and direction, indicating the overall change in an object's position. The script uses the example of a person walking to illustrate that while the distance walked is 16 meters, the displacement is only 2 meters to the east, as the person ends up there from the starting point. For back and forth motion, the script provides examples to show how to calculate both distance (by summing the lengths of each segment of the journey) and displacement (by considering the direction of each segment and using positive and negative values accordingly). The video concludes with tips for success in understanding these concepts, such as sketching a diagram to visualize the directions and numerical values.
Takeaways
- 📏 **Distance** is the total amount of ground covered by an object and is a scalar quantity, meaning it only has magnitude.
- 📍 **Displacement** is the overall change in position of an object and is a vector quantity, which includes both magnitude and direction.
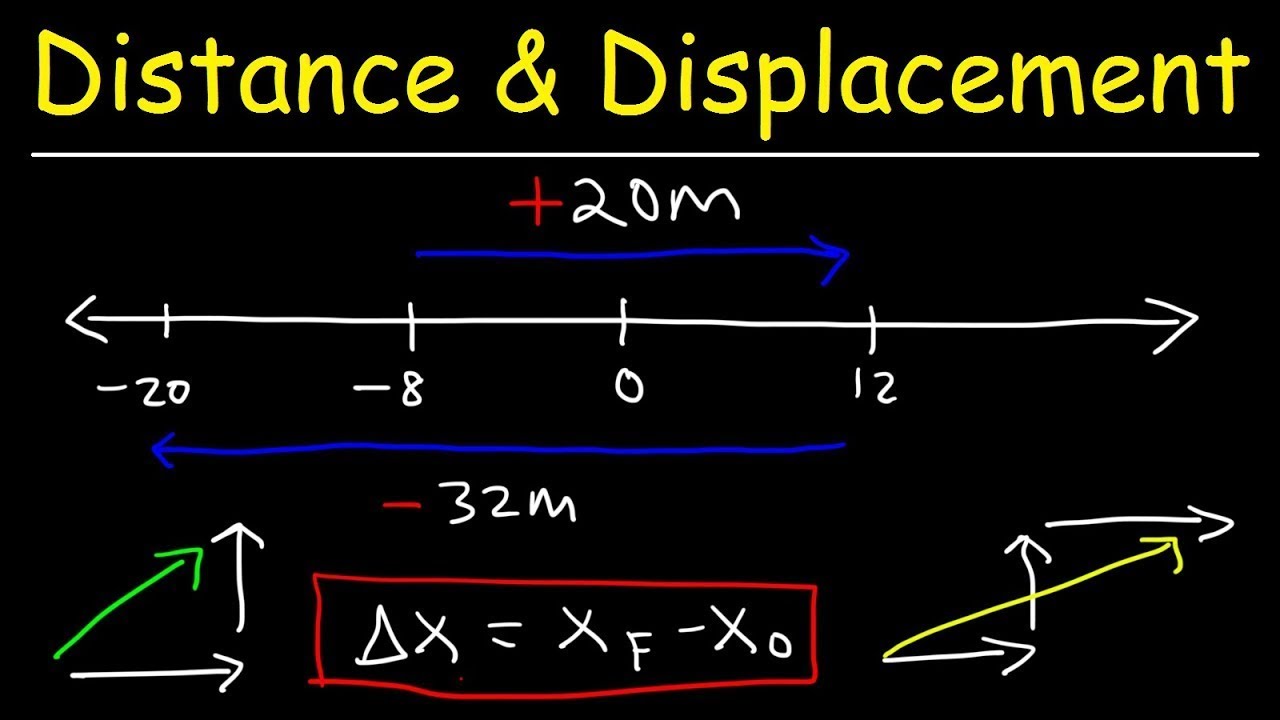
- 🔄 When an object changes direction, distance and displacement can have different numerical values.
- ↔️ Distance and displacement are the same only when an object moves in a straight line without changing direction.
- 🚶 For calculating distance in back and forth motion, add the lengths of each part of the journey without considering direction.
- 🧭 To calculate displacement, consider the direction of each part of the journey, often assigning positive and negative values to indicate direction.
- 📊 For complex back and forth motions, sketch a diagram with vector arrows representing each part of the journey, including direction and magnitude.
- ➕ Add up the lengths for distance, ignoring direction.
- ➕ Add up the vectors with their directional signs for displacement.
- 🤔 A negative displacement indicates a direction opposite to the defined positive direction.
- 🎯 Practice with interactive exercises can help solidify understanding of distance and displacement calculations.
- 👋 The video provides additional resources for practice on the described concepts.
Q & A
What is the fundamental difference between distance and displacement?
-Distance is the total amount of ground covered by an object and is a scalar quantity, meaning it only has magnitude. Displacement, on the other hand, is the overall change in position of an object and is a vector quantity, which means it has both magnitude and direction.
When do distance and displacement have the same value?
-Distance and displacement have the same value when an object moves in a straight line without changing direction. In such cases, the path taken by the object is the same as its displacement vector.
How do distance and displacement differ when an object undergoes back and forth motion?
-In back and forth motion, the distance is the sum of the lengths of all the individual segments of the motion, regardless of direction. Displacement, however, takes into account the direction of each segment and is the vector sum of these segments, which may result in a different numerical value.
How is the direction of displacement determined when calculating it?
-The direction of displacement is determined by assigning positive and negative signs to different directions. For example, one might designate eastward movement as positive and westward movement as negative. The final displacement is then the sum of these values, with the sign indicating the overall direction.
What is the distance Noah traveled in the first example with his friend Samir?
-Noah traveled a distance of 5.2 kilometers, which is the sum of the 3.2 kilometers west to Samir's house and the 2.0 kilometers east to Mickey D's.
What is the displacement of Noah in the first example with his friend Samir?
-Noah's displacement is 1.2 kilometers to the west, calculated by subtracting the eastward travel (2.0 kilometers) from the westward travel (3.2 kilometers).
How do you calculate the distance for a more complex back and forth motion like Noah's trip to pick up his friends and go to Mickey D's?
-To calculate the distance, you add up all the individual distances traveled in each segment of the trip, regardless of direction. For Noah's trip, this would be 1.4 kilometers east to Caitlyn's, 3.6 kilometers west to Waylon's, and 1.0 kilometer east to Mickey D's, totaling 6.0 kilometers.
How do you calculate the displacement for Noah's complex back and forth motion to pick up his friends and go to Mickey D's?
-You assign directions as positive or negative, then add the distances traveled in each direction accordingly. For Noah's trip, if east is positive and west is negative, the displacement would be 1.4 km (east) - 3.6 km (west) + 1.0 km (east), resulting in a displacement of 1.2 kilometers to the west.
What is the significance of the negative sign in the calculation of displacement?
-The negative sign in displacement indicates the direction of the overall change in position. If the displacement is negative, it means the final position is in the opposite direction of the chosen positive direction.
What tips are suggested for successfully calculating distance and displacement for a back and forth trip?
-Begin by sketching a diagram with vector arrows indicating the direction and approximate length of each segment. Label each arrow with its numerical value. For distance, ignore direction and add the numbers. For displacement, define positive and negative directions, include these in your addition, and translate the resulting positive or negative value into an actual direction.
Why is it important to consider both distance and displacement when analyzing motion?
-Distance provides information about the total path length traveled, which is useful for understanding the extent of motion. Displacement, by considering direction, provides information about the change in position, which is crucial for understanding the net movement and direction of an object.
How can practicing the calculation of distance and displacement through interactive exercises help in understanding these concepts?
-Interactive exercises allow for a hands-on approach to learning, enabling individuals to apply the definitions of distance and displacement in various scenarios. This practice reinforces understanding and helps solidify the concepts in a learner's mind.
Outlines
📏 Understanding Distance vs. Displacement
This paragraph introduces the fundamental concepts of distance and displacement. Distance is described as the total ground covered by an object, making it a scalar quantity that only considers magnitude. Displacement, on the other hand, is a vector quantity that considers both magnitude and direction, representing the overall change in position. The paragraph uses an animation of a man walking to illustrate the difference, where the man covers a distance of 16 meters but ends up 2 meters east of his starting point, indicating a displacement of 2 meters east. The key takeaway is that distance and displacement are only the same when an object moves in a straight line without changing direction.
Mindmap
Keywords
💡Distance
💡Displacement
💡Scalar Quantity
💡Vector Quantity
💡Direction Ignorant
💡Direction Aware
💡Back and Forth Motion
💡Positive and Negative Direction
💡Magnitude
💡Change in Position
💡Interactive Exercises
Highlights
Distance is the total amount of ground covered by an object, a scalar quantity described by magnitude or numerical value.
Displacement is the overall change in position of an object, a vector quantity with both magnitude and direction.
Scalars, like distance, are direction-ignorant, while vectors, like displacement, are always aware of direction.
When there's a change in direction, there's a difference in numerical value for distance and displacement.
Distance and displacement have the same value only when an object moves in a straight line without changing direction.
To calculate distance for back and forth motion, add the lengths of all parts of the motion, ignoring direction.
For displacement, consider the direction of each part of the motion, assigning positive and negative values accordingly.
An example given is Noah driving to pick up friends and then to Mickey D's, illustrating how to calculate distance and displacement.
Distance for Noah's trip is calculated by adding all individual distances traveled, resulting in 6.0 kilometers.
Displacement for Noah's trip is determined by adding the vectors with their respective directions, resulting in 1.2 kilometers west.
The negative sign in displacement indicates the direction towards the west.
To successfully calculate distance and displacement, sketch a diagram with vector arrows indicating direction and length.
Label each vector arrow in the diagram with its numerical value for clarity.
For distance calculations, simply add up the numerical values since it's a scalar quantity.
For displacement, define positive and negative directions, then include these in the summation of the vectors.
Translate the final positive or negative result of displacement into an actual direction like east or west.
Interactive exercises on the website can help practice and solidify understanding of distance and displacement calculations.
Mr. H provides a comprehensive explanation and tips for understanding the concepts of distance and displacement.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: