Physics 15 Torque Example 1 (1 of 7) Mass on Rod and Cable

Michel van Biezen
3 Apr 201308:24
EducationalLearning
32 Likes 10 Comments

TLDRIn this online lecture, the presenter delves into the concept of torque in statics problems, where there is no net force or torque in any direction. The example involves a vertical pole with a pivoting beam, a cable, and a hanging mass. To find the tension in the cable, a pivot point is chosen to eliminate unknown forces. The torques due to the weight of the hanging mass (mg), the weight of the beam (big mg), and the tension in the cable are identified and calculated relative to the pivot point. Using the right triangle formed by the beam and cable, the perpendicular distance (d3) is determined using the sine of the angle. The problem is solved by setting the sum of torques to zero, isolating the variable for tension, and plugging in the values for mass and angle to find the tension in the cable, which is calculated to be 2940 Newtons. The lecture concludes by encouraging further practice with more examples to master the concept of torque in statics.

Takeaways
  • 🔥 Statics problems deal with systems where everything is motionless, indicating no net forces or torques in any direction.
  • 📈 Choosing a pivot point strategically can simplify the calculation of torques by eliminating forces through the pivot point from consideration.
  • 📌 The torque is calculated by multiplying the force acting on an object by the perpendicular distance from the line of action of the force to the pivot point.
  • 📝 Summing up the torques involves considering all forces and their directions relative to the pivot point, with clockwise and counterclockwise torques often assigned positive and negative values respectively.
  • 🚨 Key forces in the problem include the gravitational force (mg) of the hanging mass and the beam, and the tension in the cable preventing the beam from falling.
  • 💡 The distances from the pivot point to where these forces act are crucial for calculating the torques (denoted as d1, d2, d3).
  • 📚 The solution hinges on setting the sum of all torques around the pivot point to zero to maintain equilibrium.
  • 📖 The lever arm distances (d1, d2, d3) can be directly related to the geometry of the setup, such as the length of the beam or angles in a triangle formed by the beam and cable.
  • 📱 Solving for the tension in the cable involves algebraically isolating the tension term and using trigonometric relationships to express distances in terms of known lengths and angles.
  • 💰 The final equation for the tension in the cable illustrates the interplay of forces and distances, showing how they collectively uphold the static equilibrium.
Q & A

  • What is the main concept discussed in the lecture?

    -The main concept discussed in the lecture is torque, particularly in the context of statics problems where there are no net forces or torques acting on a system.

  • Why is it important to choose a pivot point in statics problems?

    -Choosing a pivot point is important because it helps to simplify the problem by eliminating forces that pass through the pivot point, making them irrelevant to the calculation of torques.

  • What is the significance of the term 'statics problems' in the context of the lecture?

    -In 'statics problems', all objects are motionless, meaning there are no net forces or torques acting on them. This condition is crucial for applying the concept of torque to find solutions to such problems.

  • How does the lecturer define positive and negative torque in the context of the problem?

    -The lecturer defines clockwise torque as positive and counterclockwise torque as negative, which is an arbitrary choice as long as it is consistent within the problem.

  • What is the formula for calculating torque?

    -The formula for calculating torque is the force acting on an object times the perpendicular distance from the line of action of the force to the pivot point.

  • What are the three forces considered in the problem presented in the lecture?

    -The three forces considered are the weight of the hanging mass (mg), the weight of the beam (big mg), and the tension in the cable (T).

  • How does the lecturer determine the distance (d3) in the problem?

    -The lecturer determines d3 by using trigonometry, specifically by calculating the length of the side opposite angle theta in a right triangle formed by the cable, the beam, and the horizontal line.

  • What is the mass of the beam and the hanging mass in the problem?

    -The mass of the beam is 200 kilograms, and the mass of the hanging mass is 50 kilograms.

  • What is the length of the beam used in the problem?

    -The length of the beam is assumed to be 4 meters for the purpose of the problem.

  • What is the angle theta in the right triangle formed by the cable, the beam, and the horizontal line?

    -The angle theta is 30 degrees.

  • What is the final calculated tension in the cable?

    -The final calculated tension in the cable is 2940 Newtons.

  • Why is it unnecessary to know the actual length of the beam to solve the problem?

    -It is unnecessary to know the actual length of the beam because the equation is set equal to zero, and the length (L) cancels out from each term when divided by L.

Outlines
00:00
📚 Introduction to Torque in Statics Problems

The first paragraph introduces the concept of torque within the context of statics problems, where objects are motionless and there are no net forces or torques acting. The lecturer uses an example involving a vertical pole, a pivoting beam, a cable, and a hanging mass to illustrate how to find the tension in the cable. The process involves selecting a pivot point, identifying all relevant torques, and setting up an equation based on the principle that the sum of torques equals zero. The description includes the identification of forces acting on the beam, such as the weight of the hanging mass (mg), the weight of the beam (big mg), and the tension in the cable (T), and their respective distances (d1, d2, d3) from the pivot point.

05:01
🔍 Solving for Tension Using Torque Analysis

The second paragraph delves into the process of solving for the tension in the cable by setting up an equation that represents the sum of torques equaling zero. The lecturer assigns variables to the distances from the forces' lines of action to the pivot point (d1, d2, d3) and explains the geometric relationship that defines d3 in terms of the beam's length (L) and an angle (Theta). By substituting the known values and simplifying the equation, the tension (T) is isolated and calculated. The lecturer provides specific values for the mass of the hanging object (50 kg), the mass of the beam (200 kg), and uses the sine of 30 degrees to solve for the tension. The final calculation results in a tension of 2940 Newtons, concluding the problem-solving example.

Mindmap
Keywords
💡Torque
Torque is the rotational equivalent of linear force. It is a measure of the force that can cause an object to rotate around an axis. In the video, torque is central to solving the problem of finding the tension in a cable attached to a beam. The concept is used to balance the clockwise and counterclockwise forces acting on the beam, with the sum of all torques equaling zero in a static condition.
💡Statics Problems
Statics problems involve analyzing structures or objects that are not in motion, meaning there are no net forces or torques acting on them. The video focuses on statics problems to demonstrate how to calculate forces such as tension in a cable using the concept of torque. An example in the script involves a vertical pole with a beam and a hanging mass, illustrating a typical statics scenario.
💡Pivot Point
A pivot point is a point around which an object or system can rotate without any translation. In the context of the video, the lecturer chooses a pivot point to facilitate the calculation of torques acting on the beam. The pivot point is strategically selected to simplify the problem by eliminating forces passing through it.
💡Tension
Tension refers to the force exerted by a string, cable, or similar object when it is pulled tight by opposing forces. In the video, the main problem is to find the tension in the cable that is holding up a beam with a hanging mass. The tension is calculated by balancing it against the torques created by the weights of the beam and the hanging mass.
💡Beam
A beam is a horizontal or sloping load-bearing structure that is capable of withstanding load and transmitting it to vertical supports. In the video, the beam is attached to a vertical pole and is subjected to various forces, including its own weight, the weight of a hanging mass, and the tension from a cable. The beam's properties, such as its mass and length, are critical in the torque analysis.
💡Mass
Mass is a measure of the amount of matter in an object, and it is directly related to the gravitational force acting on the object. In the video, the mass of the beam and the hanging mass are essential components in calculating the torques and, subsequently, the tension in the cable. The masses are used to determine the gravitational forces (weight) acting at different points on the beam.
💡Center of Mass
The center of mass is the point at which the mass of an object may be considered to be concentrated for the purpose of analyzing its motion. In the video, the center of mass of the beam is mentioned as being at the midpoint of the beam, which is important for calculating the torque due to the beam's weight acting through this point.
💡Right Triangle
A right triangle is a triangle that has one angle that is a right angle (90 degrees). In the video, a right triangle is formed by the cable, the beam, and the horizontal distance from the pivot point to the point where the cable attaches to the beam. The properties of the right triangle, specifically the sine of the angle, are used to determine the distance (d3) in the torque calculation.
💡Sine of an Angle
The sine of an angle in a right triangle is the ratio of the length of the side opposite the angle to the length of the hypotenuse. In the video, the sine of an angle (theta) is used to calculate the distance (d3) from the line of action of the cable's force to the pivot point, which is necessary for determining the torque caused by the cable's tension.
💡Equilibrium
Equilibrium refers to a state in which the sum of the torques acting on an object is zero, resulting in no net rotation. In the video, the concept of equilibrium is used to set up the equation for calculating the tension in the cable, as the sum of all torques around the pivot point must be zero for the system to remain static.
💡Newtons
Newtons is the unit of force in the International System of Units (SI). It is defined as the force required to accelerate a one-kilogram mass by one meter per second squared. In the video, the final calculated tension in the cable is expressed in Newtons, which is the unit used to quantify the force exerted by the cable to support the beam and the hanging mass.
Highlights

Static problems involve scenarios where everything is motionless, with no net forces or torques in any direction.

The concept of torque is used to find the solution to statics problems involving forces and pivot points.

A vertical pole with a pivoting beam and a cable is used as an example to demonstrate how to work with torque.

Choosing the pivot point is crucial - it should eliminate any unknown forces from being material to the problem.

The sum of all torques around the pivot point must equal zero in a statics problem.

Identify and calculate the torques caused by the weight of the hanging mass, the weight of the beam, and the tension in the cable.

Use the perpendicular distance from the line of action of each force to the pivot point in your torque calculations.

Define clockwise torque as positive and counterclockwise torque as negative - consistency within the problem is key.

Sum up all the torques acting on the system, using the formula torque = force x perpendicular distance.

In the given example, the beam has a mass of 200 kg, the hanging mass is 50 kg, and the beam length is 4 meters.

The tension in the cable can be found by setting the sum of torques equal to zero and solving for the tension variable.

The distance from the cable force to the pivot (d3) can be found using trigonometry based on the angle formed by the cable.

Dividing the torque equation by the length of the beam (L) simplifies the equation without needing to know the actual length.

Solving for the tension variable gives the tension in the cable in terms of the masses, their weights, and the angle's sine.

Substitute the given values for the masses, their weights, and the angle's sine to calculate the cable tension numerically.

The final calculated tension in the cable is 2940 Newtons for the given example problem.

This example demonstrates a straightforward approach to solving torque problems in statics, which can be applied to more complex scenarios.

Additional examples will be provided to further illustrate how to work with torque in statics problems.

Transcripts

Browse More Related Video

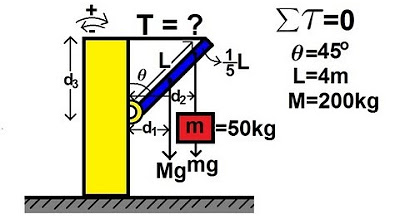
Physics 15 Torque Example 2 (2 of 7) Mass on Rod and Cable

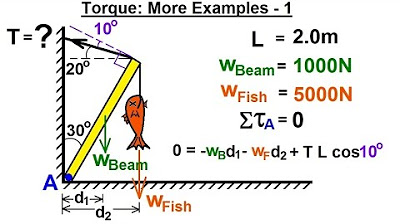
Physics 15 Torque (19 of 25) More Examples: 1 T=? of Cable Holding Fish

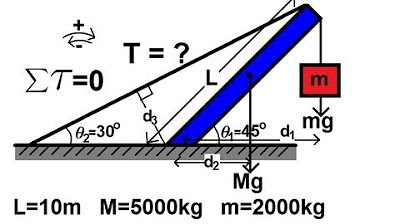
Physics 15 Torque Example 3 (3 of 7) Mass on Rod and Cable

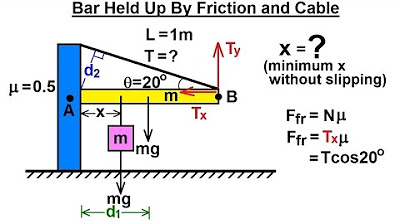
Physics 15 Torque (4 of 27) Bar Held Up by Friction

Physics 15 Torque (5 of 27) Tension=? Supporting a Gate

Physics 15 Torque (12 of 27) Example 2: Forces=? Tension=?

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Statics ProblemsTorque CalculationEngineering MechanicsOnline LectureTension AnalysisBeam DynamicsPivot PointForce DistributionProblem SolvingPhysical ConceptsEducational Content