Physics 15 Torque Fundamentals (9 of 13) How to Calculate a Torque (Basic Example 3)
TLDRThe video script demonstrates how to calculate torque on a beam subjected to a force. A force of 100 Newtons is applied at the midpoint of a 2-meter long beam, at an angle of 60° to the horizontal. To find the torque, the perpendicular distance from the force's line of action to the pivot point is determined using trigonometry, specifically the cosine of the angle formed by the hypotenuse (half the beam's length) and the adjacent side to the force's direction, which is 30°. The torque is calculated as the force multiplied by this distance, resulting in 86.6 Newton meters. The direction of the torque is counterclockwise, indicating a positive torque. The video concludes by showing how to express the torque both as a magnitude and in vector form, emphasizing its positive value in the Z direction.
Takeaways
- 🔍 **Understanding Torque**: The video explains how to calculate the torque on a beam when a force is applied at a point other than the end.
- 📐 **Beam and Force Position**: A force of 100 Newtons is applied to a 2-meter long beam at its midpoint, creating a torque.
- 📏 **Angle Theta**: The angle the beam makes with the horizontal is denoted as Theta, which is given as 60° in the example.
- 📐 **Perpendicular Distance**: The perpendicular distance from the line of action of the force to the pivot point is crucial for torque calculation.
- 🧮 **Torque Equation**: Torque is calculated using the formula: Torque = Force × Perpendicular Distance.
- 📐 **Triangle Geometry**: A right-angled triangle is formed to find the perpendicular distance, with the beam's half-length as the hypotenuse.
- 📐 **Angle F Calculation**: The complementary angle F to Theta is calculated as 90° - Theta, which in this case is 30°.
- 🧮 **Calculating Distance 'd'**: The perpendicular distance 'd' is found using the cosine of angle F and half the length of the beam.
- 🔢 **Numerical Example**: For a force of 100 N, a beam length of 2 m, and angle F of 30°, the torque is calculated to be 86.6 Newton meters.
- ➡️ **Direction of Torque**: The direction of the torque is counterclockwise, indicating a positive torque since it's the only force acting on the beam.
- 📌 **Vector Form**: The torque can be written in vector form as a positive value in the direction of the Z-axis, +86.6 Newton m.
- 📝 **Magnitude and Direction**: The final torque is expressed both in terms of its magnitude and its vector form, including direction.
Q & A
What is the concept of torque being explained in the transcript?
-The transcript explains the concept of torque as the rotational force caused by a force that is applied perpendicular to a line from the pivot point. It is calculated by multiplying the force applied with the perpendicular distance from the line of action of the force to the pivot point.
What are the given values for the force and the angle Theta in the example?
-The given values are a force of 100 Newtons and an angle Theta of 60°.
What is the length of the beam mentioned in the transcript?
-The length of the beam is given as 2 meters.
How is the perpendicular distance from the line of action of the force to the pivot point found?
-The perpendicular distance is found by using trigonometry. It is calculated as half the length of the beam (L/2) times the cosine of the angle F, where F is the complementary angle to Theta (90° - Theta).
What is the value of angle F in the example?
-Angle F is calculated as 90° - Theta, which is 90° - 60°, resulting in 30°.
What is the formula used to calculate the torque in the example?
-The formula used is Torque = Force × (L/2) × cos(F), where L is the length of the beam and F is the angle between the line of action of the force and the horizontal.
What is the calculated magnitude of the torque in the example?
-The calculated magnitude of the torque is 86.6 Newton meters (Nm).
In which direction would the force cause the beam to rotate?
-The force would cause the beam to rotate in a counterclockwise direction.
What is the sign of the torque in terms of its direction?
-The torque is positive, indicating a counterclockwise rotation.
How is the torque represented in vector form in the example?
-In vector form, the torque is represented as a positive 86.6 Newton meters in the positive Z direction.
What is the significance of the angle Theta in calculating torque?
-The angle Theta is significant as it determines the angle between the beam and the horizontal, which is essential for calculating the complementary angle F and subsequently the perpendicular distance used in the torque calculation.
Why is it important to consider the line of action of the force when calculating torque?
-Considering the line of action of the force is important because it determines the direction and point of application of the force relative to the pivot point, which directly affects the calculation of the perpendicular distance and, consequently, the torque.
Outlines
🔍 Calculating Torque on a Beam at Midpoint
This paragraph explains how to calculate the torque exerted on a beam when force is applied at its midpoint rather than at the end. Given a force of 100 Newtons, an angle of 60° (Theta), and a beam length of 2 meters, the torque is determined by multiplying the force by the perpendicular distance from the line of action of the force to the pivot point. The perpendicular distance is found using trigonometry, specifically the cosine of the complementary angle (90° - Theta), which is 30° in this case. The calculation results in a torque of 86.6 Newton-meters, with the direction being counterclockwise, indicating a positive torque. The torque is then expressed both in magnitude and vector form, with the vector pointing in the positive Z direction.
Mindmap
Keywords
💡Torque
💡Beam
💡Force
💡Angle Theta
💡Pivot Point
💡Perpendicular Distance
💡Trigonometry
💡Cosine
💡Vector Form
💡Direction of Torque
💡Newton Meters
Highlights
Calculating torque involves understanding the force applied to a beam and its distance from the pivot point.
The line of action of the force is perpendicular to the beam's direction.
The force applied is 100 Newtons, and the angle Theta is 60°.
The length of the beam is 2 meters, with the force applied at the midpoint.
Torque is calculated as the force times the perpendicular distance from the line of action to the pivot point.
The perpendicular distance is found using trigonometry within a right-angled triangle formed by the beam's length and the angles.
The hypotenuse of the triangle is half the length of the beam (l/2).
The angle F is calculated as 90° - Theta, which is 30° in this example.
The perpendicular distance (d) is found using the cosine of angle F.
The torque formula is derived as force times half the length of the beam times the cosine of angle F.
The magnitude of the torque is calculated to be 86.6 Newton meters.
The direction of the torque is counterclockwise, indicating a positive torque.
The torque vector is represented as a positive 86.6 Newton meters in the positive Z direction.
The process demonstrates the application of trigonometry in physics to solve real-world problems.
Understanding the components of torque is crucial for predicting the rotational effects of forces.
The example provides a step-by-step method to calculate torque, enhancing comprehension of the concept.
The direction of the torque is as important as its magnitude in determining the effect on a rotating object.
The vector form of torque is essential for applications where the direction of rotation is significant.
This calculation method can be applied to various engineering and physics problems involving rotational forces.
Transcripts
Browse More Related Video
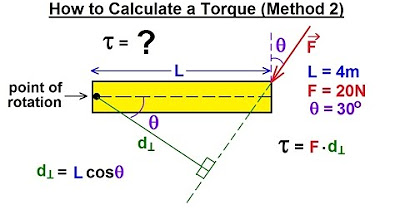
Physics 15 Torque Fundamentals (5 of 13) How to Calculate a Torque (Method 2)
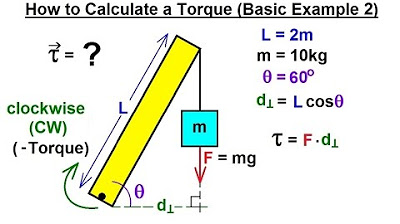
Physics 15 Torque Fundamentals (8 of 13) How to Calculate a Torque (Basic Example 2)
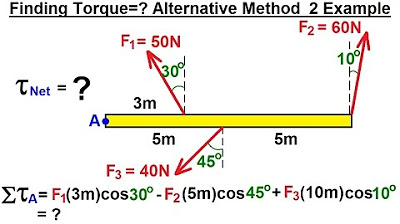
Physics 15 Torque (9 of 27) Alternative Method 1 & 2: Example Torque=?
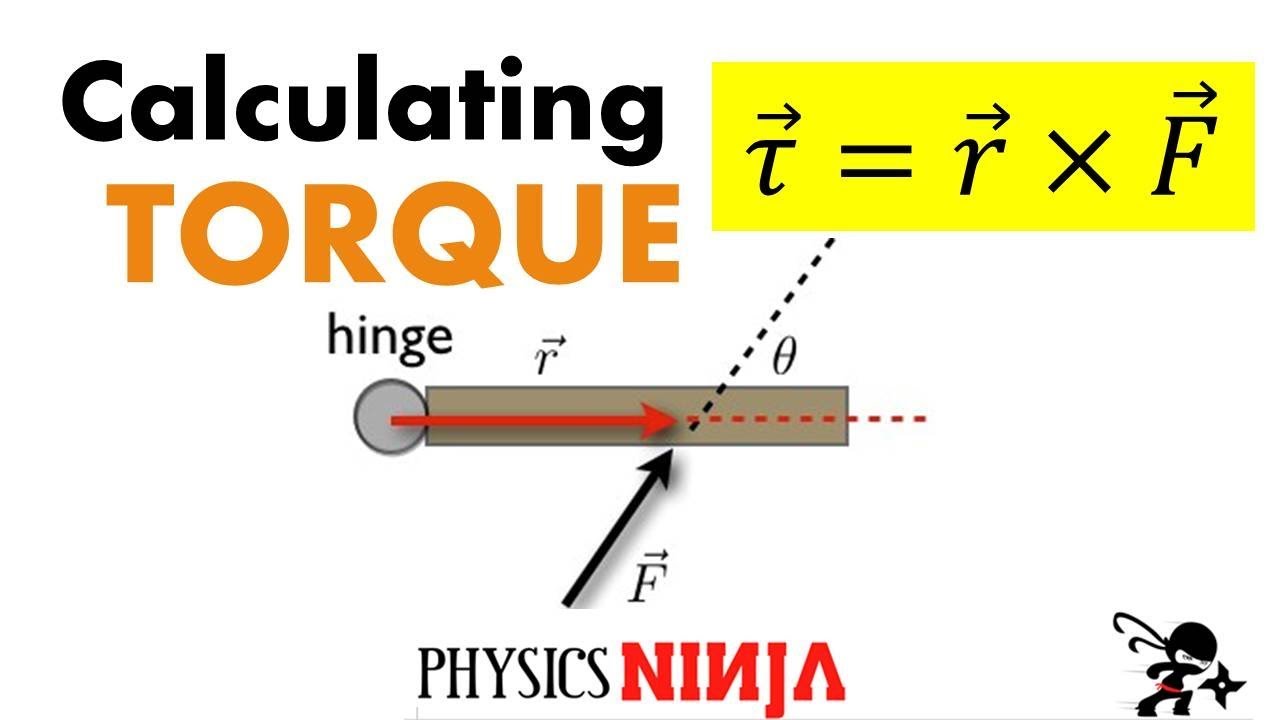
Calculating Torque

Physics 15 Torque Fundamentals (4 of 13) How to Calculate a Torque (Method 1)
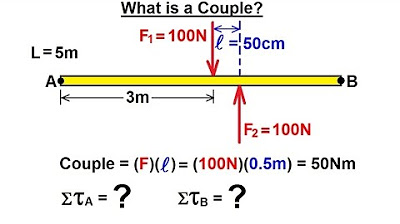
Physics 15 Torque (6 of 27) What is a Couple?
5.0 / 5 (0 votes)
Thanks for rating: