Physics 15 Torque Fundamentals (4 of 13) How to Calculate a Torque (Method 1)

Michel van Biezen
1 May 201603:36
EducationalLearning
32 Likes 10 Comments

TLDRThe lecture transcript introduces two methods for calculating torque, a measure of the force that can cause an object to rotate. The first method involves a force applied perpendicular to a position vector from the pivot point, resulting in torque equal to the product of the position vector's length, the force's magnitude, and the cosine of the angle between the force and the position vector's perpendicular. The second method accounts for situations where the force is not perpendicular, using the cosine of the angle between the force and the perpendicular to find the torque. An example calculation is provided using a force of 20 Newtons, a position vector length of 4 meters, and an angle of 30 degrees, resulting in a torque of 69 Newton meters. The summary emphasizes the importance of understanding torque's magnitude and its calculation, which is crucial in physics and engineering applications.

Takeaways
  • 🔧 **Torque Definition**: Torque is the rotational force that can cause an object to rotate or accelerate when a force is applied away from the pivot point.
  • ⚙️ **Calculation Method 1**: When force is perpendicular to the position vector, torque is calculated by multiplying the magnitude of the position vector by the magnitude of the force.
  • 📐 **Position Vector**: The position vector is the distance from the pivot point to the point where the force is applied.
  • 📈 **Angle Consideration**: If the force is not perpendicular, the torque calculation includes the cosine of the angle between the force and the perpendicular to the position vector.
  • 🔢 **Torque Formula**: Torque (τ) = Position vector (r) × Force (F) × cos(θ), where θ is the angle between the force and the perpendicular.
  • 🧮 **Example Calculation**: For θ = 30°, F = 20 Newtons, and r = 4 meters, the torque is 69 Newton meters.
  • ⚖️ **Units of Torque**: The unit of torque is Newton-meters, which represents force times distance.
  • 📌 **Direction of Force**: The direction of the applied force (whether it's clockwise or counterclockwise) does not change the method of torque calculation.
  • 🔁 **Magnitude Only**: The initial discussion focuses on the magnitude of torque, not its vector representation.
  • ⏯️ **Sequential Steps**: The script outlines a step-by-step approach to calculating torque, starting with the simplest scenario and building up to more complex situations.
  • 📚 **Further Topics**: The script hints at future discussions on vector representation of torque, suggesting a deeper exploration in subsequent lectures.
Q & A

  • What is torque in the context of physics?

    -Torque is a measure of the force that can cause an object to rotate around an axis or pivot point. It is a vector quantity that represents the rotational equivalent of linear force.

  • How is torque calculated when the force is perpendicular to the position vector?

    -When the force is perpendicular to the position vector, the torque is calculated by multiplying the magnitude of the position vector (distance from the pivot point to the point where force is applied) by the magnitude of the force.

  • What is the significance of the angle theta in calculating torque?

    -The angle theta is the angle between the force vector and the perpendicular to the position vector. It is significant because when the force is not perpendicular to the position vector, the torque is calculated using the cosine of this angle.

  • Why is the cosine function used in the formula for torque when the force is not perpendicular?

    -The cosine function is used to determine the component of the force that is perpendicular to the position vector. This is because torque is concerned with the perpendicular component of the force that contributes to the rotational effect.

  • What is the unit of torque?

    -The unit of torque is Newton meters (Nm), which represents the product of force in Newtons and distance in meters.

  • How does the direction of the force affect the calculation of torque?

    -The direction of the force does not affect the magnitude of the torque when calculated using the formula involving the cosine of the angle between the force and the perpendicular to the position vector. The magnitude of torque is dependent on the length of the position vector, the magnitude of the force, and the cosine of the angle theta.

  • In the provided example, what is the magnitude of the force applied?

    -In the provided example, the magnitude of the force applied is 20 Newtons.

  • What is the length of the object used in the example to calculate torque?

    -In the example, the length of the object, which is the position vector from the pivot point to where the force is applied, is 4 meters.

  • What is the value of the angle theta in the example?

    -In the example, the angle theta between the force vector and the perpendicular to the position vector is 30 degrees.

  • What is the calculated torque in the provided example?

    -The calculated torque in the example is 69 Newton meters, which is found by multiplying the length of the object (4 meters), the magnitude of the force (20 Newtons), and the cosine of the angle (0.866).

  • Why does the script mention that it is only dealing with the magnitudes of force and position vector?

    -The script mentions dealing only with magnitudes because the focus is on the calculation of torque without considering the direction of the force or the position vector in terms of vector quantities. Directionality or vector components will be addressed later in the context of the lecture.

  • What is the next step after calculating the magnitude of torque?

    -The next step, as hinted at in the script, is to consider the direction of the torque, which involves understanding vector components. This will provide a more comprehensive understanding of how torque affects the rotational motion of an object.

Outlines
00:00
🔧 Calculating Torque with Perpendicular Force

The first method for calculating torque is introduced when a force is applied perpendicular to the position vector from the point of rotation to the point where the force acts. The torque is calculated by multiplying the magnitude of the position vector (the length of the object) by the magnitude of the force. An example is provided where the force is 20 Newtons, the object's length is 4 meters, and the force is applied at a 30-degree angle to the vertical. Using the cosine of the angle (0.866 for 30 degrees), the torque is calculated to be 69 Newton meters. This method only deals with the magnitude of torque, not its direction.

Mindmap
Keywords
💡Torque
Torque is the rotational equivalent of linear force and represents the turning or twisting effect of a force acting on an object around an axis or pivot point. In the context of the video, it is the main theme as it explains how torque is calculated and its significance in causing an object to rotate. An example from the script is the calculation of torque when a force is applied to an object at a point not directly above the pivot point, resulting in a rotational force.
💡Position Vector
A position vector is a directed line segment that represents the position of a point in space relative to another point, typically the origin. In the video, it is used to describe the line from the point of rotation (pivot point) to the point where the force is applied. The magnitude of this vector is crucial in calculating torque, as shown when the script mentions multiplying the length of the object (position vector) by the force to find the torque.
💡Pivot Point
The pivot point is the central point around which an object can rotate. It is a fundamental concept in the video as it is the reference point for the position vector and the action of the force that results in torque. The script illustrates this with the example of an object being subjected to a force away from the pivot point, causing a torque that could lead to rotation.
💡Magnitude
The magnitude of a vector quantity, such as force or position vector, refers to its size or length without considering its direction. In the video, the magnitude is used to calculate torque by multiplying the magnitudes of the force and the position vector. The script emphasizes dealing with magnitudes rather than vector directions when performing the calculations.
💡Force
Force is a physical quantity that represents the interaction causing a change in the motion of an object. In the context of the video, force is the external input that, when applied to an object, can result in torque if not aligned with the pivot point. The magnitude of the force is a key factor in the torque calculation, as demonstrated with the given example of a 20 Newton force.
💡Angle Theta
Angle Theta (θ) is the angle between the force vector and the perpendicular to the position vector. The cosine of this angle is used in the torque calculation when the force is not perpendicular to the position vector. In the script, the angle is given as 30 degrees, and it is used to determine the torque acting on an object by multiplying the position vector's magnitude, the force's magnitude, and the cosine of theta.
💡Cosine
The cosine function, often abbreviated as cos, is a trigonometric function that describes the ratio of the adjacent side to the hypotenuse in a right-angled triangle. In the video, cosine is used to calculate the component of the force that acts perpendicular to the position vector, which is essential for determining torque. The script provides the example of calculating torque with cos(30 degrees) equal to 0.866.
💡Newton Meters
Newton meters is the unit of measurement for torque, representing the product of force in Newtons and distance in meters. It quantifies the effectiveness of a force to produce rotation. In the script, the calculated torque is expressed in Newton meters, with the example resulting in a torque of 69 Newton meters.
💡Rotation
Rotation refers to the circular movement of an object around a central point or axis. The video's theme revolves around calculating the torque, which is the force that can cause an object to rotate. The script explains that if torque is the only force acting on an object, it can cause the object to rotate or accelerate in a rotational sense.
💡Acceleration
Acceleration is the rate of change of velocity of an object with respect to time. In the context of the video, it is mentioned in relation to rotational motion, where torque can cause an object to accelerate in a rotational sense if it is the only force acting on the object. The script does not provide a direct example but implies that torque is a factor in rotational acceleration.
💡Direction
Direction refers to the course along which a force is applied or along which a vector points. While the video focuses on the magnitude of forces and vectors, the direction is crucial for understanding the action of the force relative to the position vector and the pivot point. The script notes that the direction of the force (whether it's in this direction or indirect in that direction) does not change the method of calculating torque using the cosine of the angle between the force and the perpendicular to the position vector.
Highlights

Torque can cause an object to rotate or accelerate in a rotational sense if it's the only force acting on it

Torque is calculated by multiplying the magnitude of the position vector and the magnitude of the force

The position vector is from the point of rotation to where the force is acting

If the force is perpendicular to the position vector, torque is simply the position vector length times the force

If there's an angle between the force and the position vector, use the cosine of that angle in the torque calculation

Cosine is used because we're finding the angle between the force and the perpendicular to the position vector

The direction of the force doesn't matter - torque is still position vector magnitude times force times cosine of angle

Example given: torque = (4m position vector length) x (20N force) x cos(30 degrees) = 69 Nm

Units of torque are Newton-meters, which is force times distance

Only magnitudes are considered, not the actual direction of the torque vector

This is the first method of finding torque, focusing on magnitudes

Dealing with the force perpendicular to the position vector is the simplest case for calculating torque

When the force is not perpendicular, the angle between the force and the perpendicular matters in the calculation

The angle used in the cosine function is the angle between the force and the perpendicular to the position vector, not the force and the position vector itself

The example demonstrates how to apply the formula for torque calculation when the force is at an angle to the position vector

Torque calculation involves multiplying the position vector length, force magnitude, and the cosine of the angle between them

The example provided calculates the torque as 69 Newton meters using the given values

This method is a fundamental way to calculate torque in physics and engineering

Magnitudes are considered first, with vector directions to be covered in later discussions

Transcripts

Browse More Related Video

Physics 15 Torque Fundamentals (5 of 13) How to Calculate a Torque (Method 2)

Calculating Torque

Physics 15 Torque Fundamentals (9 of 13) How to Calculate a Torque (Basic Example 3)

Physics 15 Torque Fundamentals (8 of 13) How to Calculate a Torque (Basic Example 2)

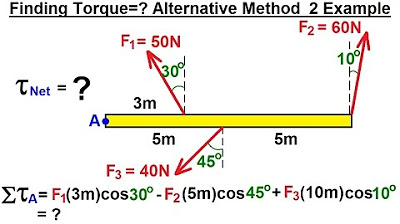
Physics 15 Torque (9 of 27) Alternative Method 1 & 2: Example Torque=?

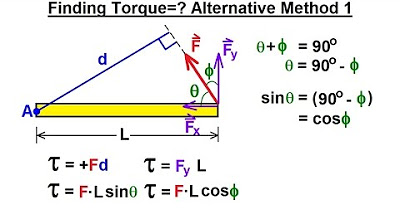
Physics 15 Torque (7 of 27) Couple: Alternative Method 1

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Torque CalculationPhysics LectureRotational DynamicsForce ApplicationPosition VectorAngular MechanicsCosine FunctionNewton's LawEngineering BasicsMathematical PhysicsEducational Content