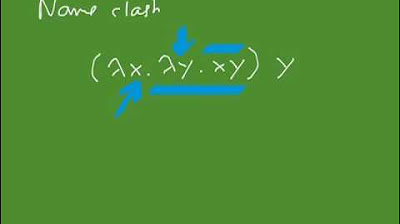Semantics: Declarative Sentences with Lambda Calculus
TLDRThis script introduces the foundational principles of Lambda calculus in linguistic semantics. It explains the role of terminal nodes in determining word meanings through the Lexicon and how non-terminal nodes are processed. The script delves into the application of Lambda expressions for transitive verbs, direct objects, and conjunctions, illustrating the semantic structure of sentences like 'Richard met Megan'. It emphasizes the importance of function application in sentence meaning, providing a clear framework for understanding how linguistics uses mathematical logic to interpret language.
Takeaways
- 📚 Lambda calculus is fundamental for understanding semantics in linguistics.
- 📝 Three guiding principles are essential for starting with basic sentences.
- 📖 Terminal nodes' meanings are specified in the Lexicon, such as words like 'John' and 'eats'.
- 🗂️ Proper names represent objects in the real world and are labeled accordingly.
- 🔄 Intransitive verbs follow the form Lambda x.x, where x represents the subject performing the action.
- ❤️ Transitive verbs, like 'loves', require two entities and follow the structure Lambda y.Lambda x.x loves y.
- ✅ Conjunctions, represented as Lambda P.Lambda Q, are true if both propositions are true.
- 🌳 Non-branching nodes pass their meaning up the tree, maintaining the same meaning as their single daughter node.
- 🔀 Branching nodes involve one daughter as a function applied to the other, determining sentence meaning.
- 🧩 Example: 'Richard met Megan' follows the rules to construct its semantic structure, resulting in R met M.
Q & A
What is the first guiding principle of Lambda calculus for semantics in linguistics?
-The first guiding principle states that if Alpha is a terminal node, then the meaning of Alpha is specified in the Lexicon. This means that the meanings of words like 'John' and 'eats' are specified in the Lexicon.
How are proper names represented in Lambda calculus?
-Proper names are represented by using the actual name of the person. This representation is not just a word but a label for the object in the real world.
What is the Lambda calculus expression for a transitive verb like 'loves'?
-The expression for a transitive verb like 'loves' is Lambda y.Lambda x.x loves y. This means we first pick up the direct object (y) and then the subject (x).
How does the meaning of a non-branching node get determined?
-For a non-branching node, the meaning of Alpha (the parent node) is the same as the meaning of Beta (the daughter node). The meaning passes up from the daughter to the parent.
What happens when a node branches into two other nodes?
-When a node branches into two other nodes, if Alpha (the parent node) has Beta and Gamma as daughters, and Beta is a function whose domain contains Gamma, then Alpha is the function Beta applied to Gamma. This means one of the daughters is a function acting on the other.
How do we apply the function in the expression Lambda y.Lambda x.x met y?
-In the expression Lambda y.Lambda x.x met y, we first apply the function to the direct object (y), and then to the subject (x). The order of application is important for resolving the Lambda expressions correctly.
What is the semantic structure for the sentence 'Richard met Megan'?
-For the sentence 'Richard met Megan', Richard is represented as 'R', Megan as 'M', and 'met' as Lambda y.Lambda x.x met y. Applying the rules, the final meaning of the sentence is Lambda x.x met M, and for the sentence node, it becomes true if 'R met M' is true.
What type of value do verb phrases and noun phrases have in Lambda calculus?
-In Lambda calculus, a verb phrase has the type ET (a function from entities to truth values), while a noun phrase has the type E (an entity).
How does the meaning of a verb phrase relate to the meaning of its components?
-The meaning of a verb phrase is a function acting on the noun phrase. For example, if the verb phrase is Lambda y.Lambda x.x met y and the noun phrase is an entity M, the verb phrase meaning becomes Lambda x.x met M.
What are the limitations of the current rules discussed in the script?
-The current rules discussed in the script can only handle basic sentences like 'Richard met Megan'. They need to be expanded to account for more complex categories and sentence structures.
Outlines
📚 Introduction to Lambda Calculus in Linguistics
This paragraph introduces the basics of Lambda calculus as it applies to semantics in linguistics. The speaker outlines three guiding principles that will be expanded upon throughout the course. The focus is on how the meaning of words and sentences is determined through the Lexicon and various rules. Terminal nodes, which represent the lowest level in a tree structure, are explained as having meanings specified in the Lexicon. Non-terminal nodes, such as noun phrases and verb phrases, require additional rules. Lexical entries for proper names, transitive verbs, and conjunctions are discussed, emphasizing the Lambda notation used to represent their meanings. The order of resolution in Lambda expressions is also highlighted, showing how the meaning of a sentence is constructed from the meanings of its components.
🔍 Semantic Structure of Sentences Using Lambda Calculus
In this paragraph, the speaker delves deeper into how Lambda calculus is used to construct the semantic structure of sentences. The example of the sentence 'Richard met Megan' is used to illustrate the process. The speaker explains how the meanings of the proper names 'Richard' and 'Megan' are represented, and how the transitive verb 'met' functions in the sentence. The concept of function application is introduced, showing how the verb phrase acts on the noun phrase to produce a truth value. The paragraph concludes with the construction of the sentence's meaning using Lambda notation, demonstrating how the sentence is true if and only if Richard met Megan. This detailed explanation provides a clear understanding of how complex sentences can be broken down and analyzed using Lambda calculus.
Mindmap
Keywords
💡Lambda Calculus
💡Terminal Node
💡Lexicon
💡Lambda Expression
💡Non-Branching Node
💡Branching Node
💡Function Application
💡Conjunctions
💡Truth Conditions
💡Transitive Verb
Highlights
Introduction to basic Lambda calculus for semantics in linguistics.
Three guiding principles for understanding semantics are introduced and will be expanded upon throughout the course.
Explanation of the first rule: terminal nodes' meanings are specified in the Lexicon.
Terminal nodes represent the bottom of the trees, such as words like 'John' and 'eats'.
Lexical entries for proper names use the actual name of the person.
Transitive verbs are represented with Lambda expressions, such as Lambda x.x dies.
Explanation of Lambda order in terms of love, emphasizing the order of subject and object.
Conjunctions are represented with Lambda expressions that require both propositions to be true.
Lexical entries are inserted into trees to determine the meanings of sentences.
Non-branching nodes pass up the meaning of their single daughter node.
Branching nodes involve function application, where the verb phrase acts on the noun phrase.
Demonstration of semantic structure construction for the sentence 'Richard met Megan'.
Explanation of how to apply Lambda expressions to construct the meaning of a sentence.
The final semantic representation of 'Richard met Megan' is Lambda x.x met Megan.
The course will expand these rules to account for more complex sentence structures.
Current rules are limited but form the foundation for more advanced semantic analysis.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: