3.5 - Max-Min Problems and Applications
TLDRThe video script presents a comprehensive guide on applying maximization and minimization techniques to solve real-world problems. It begins with an abstract exploration of these concepts, introducing the first and second derivative tests and their role in identifying critical points for functions. The script then delves into practical applications, emphasizing the importance of constraints in real-life scenarios, such as resource limitations. It illustrates the process of maximizing or minimizing quantities subject to constraints, using calculus techniques to find absolute maximum and minimum values. The transcript walks through solving systems of equations, applying substitution methods, and differentiating to find critical values. It also discusses verifying these points as true maxima or minima through the behavior of the derivative. The script provides step-by-step examples, including geometric problems like maximizing the area of a fenced rectangle with limited fencing and minimizing the surface area of an open-top rectangular metal tank with a fixed volume. It concludes with a financial application, demonstrating how to maximize profit by determining the optimal number of units to produce and sell, given a pricing function and fixed costs. The video is an invaluable resource for those looking to apply calculus to everyday problems, showcasing the versatility and power of maximization and minimization strategies.
Takeaways
- 📈 Maximization and minimization are crucial for real-world applications where resources are finite and we seek to optimize outcomes.
- 🔍 The general approach to solving maximization/minimization problems involves using calculus techniques like derivatives to find critical values.
- 🌟 To apply these techniques, constraints on variables are combined with the objective function to create a system of equations.
- 🧠 Substitution is a common method to isolate one variable and express the quantity in terms of another, simplifying the problem.
- 📌 The first derivative test is used to identify potential maximum or minimum values by setting the derivative equal to zero and solving for the variable.
- 📊 The sign of the derivative to the left and right of a critical value helps determine if it corresponds to a maximum, minimum, or neither.
- 🏛 In geometric problems, the technique can be used to maximize areas or minimize surface areas, given certain constraints.
- 📦 For physical applications, such as constructing a container with a specific volume, the method involves expressing the surface area in terms of one variable and then finding the dimensions that minimize it.
- 💰 In financial scenarios, the same principles apply to maximize profit by determining the optimal number of units to produce and sell based on cost and revenue functions.
- ✅ Verification of the maximum or minimum is essential by analyzing the behavior of the derivative around the critical value.
- 🔑 The power of these strategies lies in their versatility, allowing for optimization in a wide range of contexts beyond just mathematical problems.
Q & A
What are the two primary techniques discussed in the video for finding maximum and minimum values?
-The video discusses the first and second derivative tests as the primary techniques for finding maximum and minimum values.
What is the general approach to using maximization and minimization techniques in real-world problems?
-The general approach involves identifying the quantity to be maximized or minimized, understanding the constraints on the resources, and applying calculus techniques such as taking derivatives to find critical values where maxima or minima occur.
In the context of the video, what are the two goals when dealing with maximization or minimization problems?
-The two goals are to find the maximum or minimum value of a specified quantity and to determine the values of the inputs or components that lead to this maximum or minimum value.
How does the video approach the problem of maximizing the quantity q, where q equals x times y squared, with the constraint x plus y squared equals one?
-The video uses substitution to isolate one variable, taking the derivative with respect to the remaining variable, and setting it to zero to find critical values. It then checks these critical values to determine the maximum value of q.
What is the significance of using the second derivative test in the context of the video?
-The second derivative test is used to determine whether a critical point is a maximum, minimum, or neither. It provides additional information about the concavity of the function around the critical point.
How does the video demonstrate the application of maximization and minimization techniques in a geometric problem?
-The video provides an example of a hobby store using a limited amount of fencing to fence off a rectangular area. By applying the maximization technique, it finds the dimensions that maximize the area enclosed by the fencing.
What is the role of constraints in applied problems involving maximization and minimization?
-Constraints define the limitations on resources or conditions that must be met. They are crucial as they limit the possible solutions and are used to transform the problem into an equation or system of equations that can be solved using calculus techniques.
How does the video approach the problem of minimizing the surface area of an open-top rectangular metal tank with a fixed volume?
-The video uses the given volume constraint to express one variable in terms of another, then substitutes this expression into the surface area equation to create a single-variable function. It then finds the derivative, sets it to zero to find critical points, and verifies these points to determine the minimum surface area.
What is the importance of verifying the critical points found in the maximization and minimization problems discussed in the video?
-Verification is essential to ensure that the critical points found indeed correspond to a maximum or minimum. This is done by examining the sign of the derivative on either side of the critical point, which indicates whether the function is increasing or decreasing.
In the financial situation discussed in the video, how is the pricing function used to determine the price per unit of a stereo system?
-The pricing function, defined as p(x) = 1000 - x, is used to calculate the price per unit based on the number of units (x) the company intends to sell. As the number of units increases, the price per unit decreases, following the function's rule.
How does the video demonstrate the process of maximizing profit in a financial context?
-The video demonstrates this by first defining the cost and revenue functions based on given data, then deriving the profit function. It finds the derivative of the profit function, sets it to zero to find critical points, and uses these points to determine the number of units that need to be produced and sold to maximize profit.
Outlines
📚 Introduction to Maximization and Minimization Techniques
This paragraph introduces the topic of applying maximization and minimization techniques to solve real-world problems. It emphasizes the importance of using calculus methods, such as the first and second derivative tests, to find the absolute maximum or minimum values of quantities subject to constraints. The focus is on practical applications where resources are limited, and the goal is to maximize or minimize outcomes, like cost or area, within those constraints.
🔍 Maximizing a Quantity with Given Constraints
The paragraph discusses a method for maximizing a quantity, represented by q = x * y^2, subject to the constraint x + y^2 = 1 with x and y being positive numbers. The process involves isolating one variable, substituting it into the equation to eliminate it, and then differentiating the resulting single-variable equation to find critical points. The critical points are then analyzed to determine the maximum value of q, taking into account the original constraints.
🔢 Solving for Critical Values and Verifying Maxima
This section details the process of finding critical values by setting the derivative equal to zero and solving for the variable y. It explains how to factor out common terms and solve the resulting equations to find potential maximum or minimum points. The paragraph also highlights the need to verify that a critical point indeed represents a maximum by examining the sign of the derivative on either side of the critical value.
📏 Application: Maximizing a Rectangular Area with Limited Resources
The paragraph presents a practical application where a hobby store aims to maximize the area of a rectangular space fenced off with a limited amount of fencing. It describes the step-by-step process of setting up the problem, drawing a diagram, listing known information, and formulating the area as a function of one variable. The goal is to find the dimensions that maximize the area given the constraint of a fixed perimeter.
📦 Minimizing Surface Area for a Rectangular Tank with a Fixed Volume
The paragraph explores the problem of minimizing the surface area of an open-top rectangular tank with a fixed volume. It outlines the process of calculating the surface area for the given dimensions and expressing the volume as a function of the dimensions. The goal is to find the dimensions that minimize the surface area while maintaining the required volume.
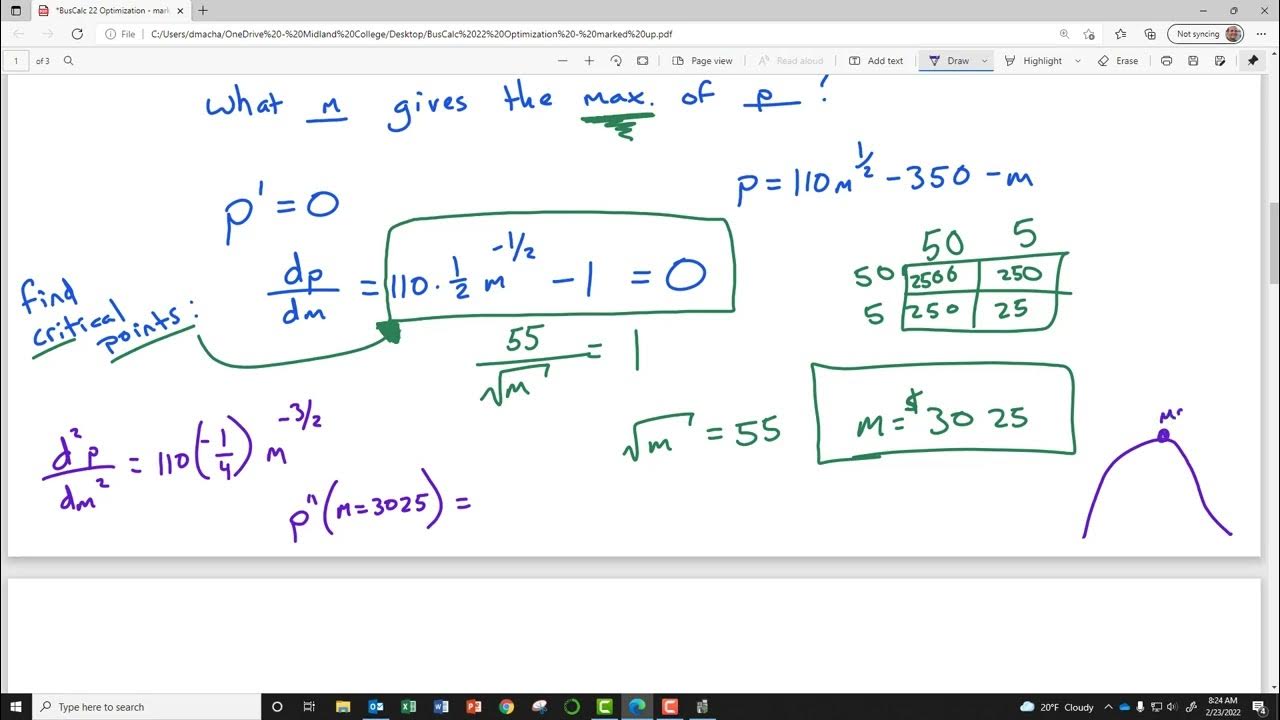
📈 Financial Application: Maximizing Profit by Adjusting Production and Pricing
This section discusses a financial scenario where a car audio company seeks to maximize profit by determining the optimal number of stereos to produce and sell. It involves creating functions for cost, revenue, and profit based on a pricing function and fixed and variable costs. The paragraph explains how to find the critical point for profit maximization and verify it using the derivative.
💰 Conclusion on Maximizing Profit and Pricing Strategy
The final paragraph concludes the financial application by calculating the exact profit for producing and selling 490 units, which is identified as the optimal number to maximize profit. It also determines the price per unit that should be set to achieve this profit, based on the given pricing function.
Mindmap
Keywords
💡Maximization
💡Minimization
💡Derivative
💡Constraint
💡Critical Value
💡Substitution
💡First and Second Derivative Tests
💡Geometric Problems
💡Linear Function
💡Profit Function
💡Pricing Function
Highlights
The video covers the application of maximization and minimization techniques using calculus, focusing on real-world problems.
Discussion on the general approach to using derivative tests for constrained optimization problems.
Introduction to the concept of finite resources and scarcity, emphasizing the importance of maximizing or minimizing quantities within these constraints.
The goal of finding the maximum or minimum value of a quantity, which could be abstract or specific to a situation.
The strategy of using calculus to find critical points where maxima or minima occur by setting derivatives to zero.
Technique of substitution to transform a system of equations into a single-variable function for easier differentiation.
Example of maximizing the quantity 'q' subject to the constraint x + y^2 = 1, where x and y are positive numbers.
Use of the power rule to find the derivative of a function in terms of a single variable.
Process of factoring and solving for critical values where the derivative equals zero.
Verification of maxima or minima by analyzing the sign of the derivative on either side of the critical point.
Application of the maximization technique to a geometric problem involving fencing and area optimization.
Method of reverse substitution to find associated variable values after identifying the critical point for optimization.
Example of minimizing the surface area of a rectangular metal tank with a fixed volume.
Explanation of how to handle constraints by expressing the quantity to be optimized in terms of a single variable.
Demonstration of how to use calculus to find the dimensions that maximize or minimize a given quantity.
Application of optimization techniques to real-world scenarios, such as maximizing profit in a financial context.
Use of a pricing function to determine the price per unit based on the number of units sold.
Construction of cost, revenue, and profit functions to identify the optimal number of units to produce for maximum profit.
Strategy for confirming the maximum profit point by examining the behavior of the derivative around the critical value.
Calculation of the price to charge per unit to achieve the maximum profit based on the pricing model.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: