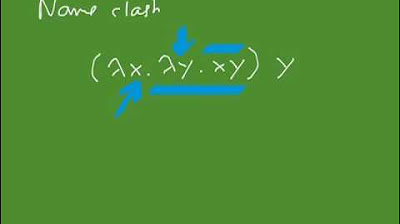The Lambda Calculus, part 1 2 Applied lambda calculi; the simply typed lambda calculus
TLDRThe video script delves into the applied lambda calculus, focusing on the simply typed lambda calculus which incorporates a type system for enhanced computation modeling. It explains the syntax, semantics, and type system, including type judgments and rules for constants, abstractions, and applications. The script highlights the utility of type systems in classifying well-typed programs and ensuring safety and termination, showcasing the simply typed lambda calculus as a foundational concept in programming language theory.
Takeaways
- 📚 The script discusses Applied Lambda Calculus, specifically the Simply Typed Lambda Calculus, which extends the Pure Lambda Calculus with a type system.
- 🔢 The Pure Lambda Calculus is foundational, with capabilities to encode natural numbers and truth values, despite its simplicity involving only variables, abstractions, and applications.
- 💡 The concept of adding constants to Lambda Calculus as primitives is introduced to avoid the need for coding up certain constructs like natural numbers or truth values.
- 📝 The Applied Lambda Calculus incorporates constants and functions with a specific number of arguments, which are part of the syntactic category called 'lambda comp'.
- 🔄 The semantics of the Applied Lambda Calculus can be extended with separate reduction rules for new constants or by using an 'apply' function with defining clauses.
- 🔑 The Type System originates from logic and is integral to programming languages, providing a way to classify programs into well-typed and not well-typed categories.
- 🤖 Type systems are useful for early error detection in programming, with type checking being an algorithmic process to ensure a program is well-typed.
- 📉 The Simply Typed Lambda Calculus includes constructs like pairs, conditionals, and local declarations, with constants like numerals, 'plus', 'quality', 'test for zero', and boolean values.
- 📌 The operational semantics of the Simply Typed Lambda Calculus is defined by small-step semantics, where expressions evolve in single steps to reach normal form.
- 🔒 The type safety of the Simply Typed Lambda Calculus ensures that well-typed expressions remain well-typed during evaluation (Subject Reduction) and are strongly normalizing if recursion-free.
- 🚀 The script hints at the limitations of the Simply Typed Lambda Calculus and suggests a continuation of the discussion in a subsequent part, possibly to address these limitations.
Q & A
What is the main topic discussed in this script?
-The main topic discussed in this script is the applied lambda calculus, with a focus on the simply typed lambda calculus, its syntax, semantics, and type system.
Why was the applied lambda calculus developed?
-The applied lambda calculus was developed to add constants and functions as primitives to the pure lambda calculus, making it more expressive and convenient for programming without having to code up certain constructs from scratch.
What are the basic components of pure lambda calculus mentioned in the script?
-The basic components of pure lambda calculus mentioned are variables, abstractions, and applications.
How does the applied lambda calculus extend the pure lambda calculus?
-The applied lambda calculus extends the pure lambda calculus by introducing constants and an apply function, which allows for the definition of new syntactic categories and the addition of constructs like numerals, truth values, and recursion as primitives.
What is a type system and where did the concept originate?
-A type system is a way to classify programs into well-typed and not well-typed categories, ensuring safety and correctness. The concept originated in logic and is associated with the work of Bertrand Russell and Alfred North Whitehead in 'Principia Mathematica' from 1903, and later with Alonzo Church's work on the simply typed lambda calculus in 1940.
What are the two main benefits of using a type system in programming languages?
-The two main benefits of using a type system are type checking, which ensures that a program is well-typed before execution, and type inference, which helps determine the type of a program if it can be well-typed, often used in languages like Haskell and ML family languages.
What is the difference between type checking and type inference?
-Type checking is the process of determining if a given program has a specific type in a given type environment, while type inference is about determining if a program can be well-typed at all and, if so, what its type is.
What are the syntactic categories included in the simply typed lambda calculus?
-The syntactic categories in the simply typed lambda calculus include variables, abstractions, applications, pairs of expressions, conditionals (if-then-else), and local declarations (let expressions).
What is the significance of the 'apply' function in the applied lambda calculus?
-The 'apply' function in the applied lambda calculus is significant as it allows for the application of constants to their arguments, enabling the evaluation of expressions involving these constants according to predefined rules.
What are the two key results often sought after when discussing type systems?
-The two key results often sought after are type preservation (also known as subject reduction), which ensures that well-typed programs remain well-typed during evaluation, and a safety result, which varies depending on the type system but generally guarantees some form of safety for well-typed programs.
What is strong normalization and why is it a desirable property in the context of the simply typed lambda calculus?
-Strong normalization is a property that guarantees that an expression will eventually reach a normal form, meaning it will terminate and not result in an infinite reduction sequence. This is a desirable property because it ensures that well-typed expressions in the simply typed lambda calculus will always terminate, providing a form of safety.
How does the script mention handling recursion in the simply typed lambda calculus?
-The script mentions handling recursion through the introduction of 'let rec' expressions, which allow for recursive definitions where the defined function can occur within its own body, enabling recursive behavior.
What is the role of the signature in the simply typed lambda calculus?
-The role of the signature in the simply typed lambda calculus is to assign types to constants, indicating the types that these constants should have according to the type system.
Outlines
📚 Introduction to Applied Lambda Calculus
The first paragraph introduces the concept of applied lambda calculus, highlighting its evolution from pure lambda calculus. It explains that pure lambda calculus, consisting of variables, abstractions, and applications, is a universal model of computation equivalent to Turing machines. The speaker then discusses the rationale behind adding constants as primitives to the lambda calculus, which is the basis of applied lambda calculus. The paragraph also touches on the idea of extending semantics with constants and the concept of an 'apply' function, setting the stage for a more in-depth discussion on type systems and their origins in logic.
🔍 The Utility of Type Systems
In this segment, the speaker delves into the purpose and utility of type systems, which classify programs into well-typed and not well-typed categories. Type systems are integral in programming languages, serving as a pre-processing step for type checking. The speaker explains the necessity for type systems to be effective, meaning there must be an algorithm to determine if a program is well-typed. The distinction between type checking and type inference is also clarified, with the latter being a central feature in languages like Haskell and ML, which attempt to deduce the type of a program rather than requiring explicit type information.
🌟 Syntax and Semantics of Simply Typed Lambda Calculus
The third paragraph presents the syntax of the simply typed lambda calculus, which includes variables, abstractions, applications, and additional constructs like pairs, conditionals, and local declarations. The speaker emphasizes that these constructs are essentially constants in the lambda calculus. The semantics of the calculus are discussed, focusing on small-step semantics and value transitions. The rules for function application, including beta reduction and constant application, are introduced, illustrating how expressions evolve in the calculus.
🔑 Type Assignment and Judgments in Simply Typed Lambda Calculus
This paragraph explores the type system of the simply typed lambda calculus, starting with the definition of types such as 'int', 'bool', and arrow and product types. The speaker discusses the role of a type environment, which is a partial function assigning types to variables within an expression. Type judgments are then defined, explaining how types are assigned to different syntactic elements of the language using a set of type rules. The speaker provides examples of type rules for variables, pairs, functions, applications, and conditionals, illustrating how type safety is ensured in the calculus.
🔄 Recursive Definitions and Type Safety
The fifth paragraph introduces the concept of recursive definitions in the simply typed lambda calculus, allowing for the creation of recursive functions through 'let rec' expressions. The semantics for these recursive definitions are explained, showing how the definition of a function can be substituted within its own body to achieve recursion. The type rule for 'let rec' is also discussed, ensuring that the type of the recursive definition matches the type of the body of the function. The speaker emphasizes the importance of type safety in avoiding undefined operations, such as applying 'plus' to non-numeric values.
🛡️ Type Preservation and Strong Normalization
The final paragraph discusses two key results related to the type system of the simply typed lambda calculus: type preservation (subject reduction) and strong normalization. Type preservation ensures that well-typed programs remain well-typed throughout evaluation, while strong normalization guarantees that well-typed, recursion-free expressions will always terminate and reach a normal form. The speaker notes that these properties are desirable in any type system and highlights the limitations of the simply typed lambda calculus, suggesting a continuation of the discussion in future parts of the presentation.
Mindmap
Keywords
💡Applied Lambda Calculus
💡Simply Typed Lambda Calculus
💡Type System
💡Type Checking
💡Type Inference
💡Constants
💡Abstraction
💡Application
💡Type Environment
💡Strong Normalization
Highlights
Introduction to applied lambda calculus and its evolution from pure lambda calculus.
Explanation of pure lambda calculus as a universal model of computation equivalent to Turing machines.
Discussion on the rationale behind adding constants to lambda calculus for efficiency.
Description of the syntax in applied lambda calculus, including variables, abstractions, application, and constants.
Introduction of the 'apply' function for handling constants in lambda calculus.
Historical context of type systems, starting from Bertrand Russell's work in 'Principia Mathematica'.
Connection between Church's work on simply typed lambda calculus and modern programming languages.
Definition of type systems, including abstract syntax, syntactic categories, and type judgments.
Importance of type systems in classifying programs and their role in pre-processing in programming languages.
Explanation of type checking and type inference as two fundamental notions in type systems.
Syntax of the simply typed lambda calculus, including variables, abstractions, application, and additional constructs.
Semantics of the simply typed lambda calculus using small step semantics and value concepts.
Detailed rules for function application and constant application in the semantics.
Introduction to pair expressions and let expressions in the simply typed lambda calculus.
Type formation rules for simple types, including int, bool, arrow types, and product types.
Type judgments and environments in the simply typed lambda calculus and their role in typing expressions.
Recursive let definitions and their handling in the semantics and type rules.
Type safety results for the simply typed lambda calculus, including type preservation and strong normalization.
Limitations of the simply typed lambda calculus and the anticipation of further exploration in subsequent parts.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: