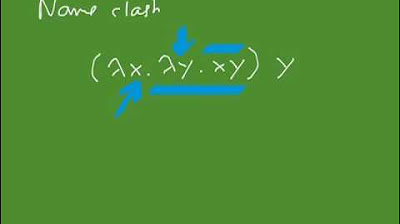Lambda Calculus vs. Turing Machines (Theory of Computation)
TLDRThis talk explores the theory of computation, delving into axiomatic thinking and the foundational axioms of mathematics. It introduces concepts like Turing machines, lambda calculus, and the Church-Turing thesis, highlighting how simple axioms can build complex computational models. The speaker also discusses the evolution of programming languages and their relation to computational axioms, emphasizing the importance of understanding foundational principles in computing.
Takeaways
- 📚 The speaker expresses great excitement about discussing the theory of computation, indicating its profound impact on their understanding of the field.
- 🔢 The concept of axiomatic thinking is introduced, emphasizing the foundational rules of mathematics that are taken for granted, such as the operation of addition and multiplication.
- 🧠 The speaker underscores the mind-blowing nature of understanding these foundational concepts, suggesting a deep cognitive shift in their comprehension of computation.
- 🏛️ The 'Tale of Two Towers' metaphor is used to describe the foundational axioms and the derived rules or 'theorems' that build upon them in the field of mathematics.
- 🎓 Giuseppe Peano's axioms for natural numbers are highlighted, showcasing a minimal set of self-evident truths from which all of mathematics can be derived.
- 🔄 The notion of syntactic sugar is explained, illustrating how certain mathematical expressions are simplified for convenience without changing their underlying meaning.
- 🤖 Alan Turing's Turing machines are introduced as a fundamental model of computation, demonstrating that complex algorithms can be reduced to simple, mechanical processes.
- 🪄 Alonzo Church's lambda calculus is presented as an alternative axiomatic system for computation, showing that computation can be expressed through function definitions and applications alone.
- 🔁 The Y Combinator in lambda calculus is explained as a method to create recursion from basic function constructs, highlighting the power of simple axiomatic systems.
- 💡 The Church-Turing thesis is mentioned, asserting the equivalence of these different models of computation and their ability to capture the concept of 'computation'.
- 🛠️ The practical implementation of Turing machines through the von Neumann architecture is discussed, showing how theoretical models can be translated into physical computing devices.
Q & A
What is the main theme of the talk on the theory of computation?
-The main theme of the talk is to explore the foundational concepts of computation, focusing on axiomatic thinking and the development of axiom towers in the context of two significant models: Turing machines and lambda calculus.
What is axiomatic thinking and why is it important in the theory of computation?
-Axiomatic thinking is a method of building a system of knowledge based on a set of non-contradictory rules or axioms. It is important in the theory of computation because it provides a structured and logical foundation for understanding how computation is defined and operates.
What are the two foundational models of computation discussed in the script?
-The two foundational models of computation discussed are Turing machines and lambda calculus.
What is the significance of the Turing machine in the history of computing?
-The Turing machine, proposed by Alan Turing, is significant because it provides a theoretical model of computation that demonstrates what can be computed. It is considered the foundation of modern computer science and the basis for the Church-Turing thesis.
What is lambda calculus and why is it important?
-Lambda calculus is a formal system for function definition, manipulation, and application. It is important because it provides an alternative axiomatic system for computation that is equivalent to the Turing machine in expressive power, despite its different approach and lack of explicit notions of state or loops.
What is the Church-Turing thesis and what does it claim?
-The Church-Turing thesis is a hypothesis that asserts that any function that is computable by an algorithm can be computed by a Turing machine, and vice versa. It claims that the models of computation proposed by Church (lambda calculus) and Turing are equivalent and sufficient to describe all computable functions.
What is the von Neumann model and how does it relate to the physical implementation of computing?
-The von Neumann model is a framework for computer architecture that includes a memory, a central processing unit (CPU) with a control unit and a logic unit, and a set of instructions for the CPU to interact with memory. It relates to the physical implementation of computing by providing a blueprint for how computers can be built to perform computations based on the theoretical foundations of Turing machines.
What is the difference between imperative and functional programming paradigms as discussed in the script?
-Imperative programming, as exemplified by the Turing machine and von Neumann model, involves modifying state and using constructs like loops and conditionals. Functional programming, as seen in lambda calculus, relies on pure functions and immutable data, avoiding side effects and promoting the use of recursion and higher-order functions.
What is the significance of the Y Combinator in lambda calculus?
-The Y Combinator is significant in lambda calculus because it allows for the creation of recursive functions without the need for explicit recursion constructs. It demonstrates the power of lambda calculus to build complex computational patterns from simple axioms.
How does the script relate the concepts of computation to modern programming practices and languages?
-The script draws parallels between the foundational concepts of computation and modern programming practices, such as the use of one-way data flow in React and Redux, which is a natural outcome of the constraints inherent in lambda calculus. It suggests that understanding these foundational concepts can provide insights into why certain programming paradigms and languages work the way they do.
What is the role of syntactic sugar in the context of the script?
-Syntactic sugar refers to convenience rules or symbols that simplify programming language syntax without adding new expressive power. In the script, it is used to illustrate how certain concepts, like numbers and operations, can be reduced to more primitive forms defined by axioms, making computation more manageable without changing its fundamental nature.
Outlines
📚 Introduction to the Theory of Computation
The speaker expresses great excitement about discussing the theory of computation, a topic they first encountered as an undergraduate at UCLA. Initially finding the subject challenging, the speaker has since come to appreciate its profound implications. The talk is framed as 'A Tale of Two Towers,' with an emphasis on axiomatic thinking, a formal approach to mathematics that may seem unconventional. The speaker uses the example of basic arithmetic operations to illustrate the concept of axioms and theorems, explaining how operations like multiplication can be defined in terms of addition, thereby establishing a foundation for understanding the fundamental rules of mathematics.
🔢 Axiomatic System and the Peano Axioms
The speaker delves into the concept of axiomatic systems, focusing on the Peano axioms as a minimal set of rules that define natural numbers. They explain the axioms, which include the definition of zero, equality, and the successor function, and how they can be used to construct all of mathematics. The axioms are presented as self-evident truths, and the speaker discusses the idea of syntactic sugar, which simplifies complex expressions without adding new information. The summary also touches on the process of defining addition and multiplication based on these axioms.
🌐 Axiom Towers and Their Utility
The concept of 'axiom towers' is introduced, which represents a foundational set of axioms with additional constructs built on top. The speaker discusses the idea that axioms are not inherently special but can vary in their usefulness. They provide examples of different axiom towers, such as Roman numerals and non-Euclidean geometries, to illustrate the point that some axiomatic systems may be less practical than others. The speaker also emphasizes that axiom towers don't necessarily have to correspond to reality, and that the symbols and rules within them are intrinsically linked.
🤖 Turing Machines and the Foundations of Computation
The speaker describes Alan Turing's work on Turing machines, which serve as a foundational axiom for computation. Turing machines are conceptualized as an infinitely long tape, a head that can read and write, and a set of instructions for computation. The speaker explains that Turing demonstrated the power of these machines by showing that any computable function can be computed by a Turing machine. They also mention the Brainfuck programming language as a virtual implementation of a Turing machine and provide examples of how simple algorithms, like addition, can be implemented using this model.
🎲 Turing Completeness and the Power of Simplicity
The speaker explores the concept of Turing completeness, which refers to the ability of a system to perform any computation that can be performed by a Turing machine. They provide examples of diverse systems, such as Conway's Game of Life, Magic: The Gathering, and Microsoft PowerPoint, that have been shown to be Turing complete. The speaker emphasizes the surprising power of simple axiomatic systems to represent complex computations.
📘 Lambda Calculus: An Alternative Axiom for Computation
The speaker introduces lambda calculus as an alternative axiomatic system for computation, developed by Alonzo Church. They explain the basic constructs of lambda calculus, including variables, function definitions, and function application. The speaker highlights the simplicity and elegance of lambda calculus, which can be used to represent complex computational processes despite its foundational simplicity.
🤝 The Church-Turing Thesis and Computational Equivalence
The speaker discusses the Church-Turing thesis, which posits that any function that can be computed by a Turing machine can also be computed by a lambda calculus expression, and vice versa. They explain that although Turing machines and lambda calculus were developed independently, they were found to be equivalent in terms of their computational power. The speaker also touches on the implications of this thesis for the study of computation and the development of programming languages.
🛠 The von Neumann Model and the Physical Realization of Computation
The speaker describes the transition from theoretical models of computation to their physical realization in the form of computers. They discuss John von Neumann's contributions to the design of computing machines, which included the concept of memory (RAM) and a central processing unit (CPU) with a control unit and a logic unit. The speaker also explains how the von Neumann model laid the groundwork for the development of higher-level programming languages and the abstraction of machine instructions.
🌟 The Evolution of Programming Languages and Their Foundations
The speaker traces the evolution of programming languages from assembly language to modern languages like C++, highlighting how each new language introduced higher-level constructs that could be reduced to the underlying von Neumann machine instructions. They emphasize that despite the increasing abstraction, all programming languages ultimately boil down to the fundamental axioms of computation as defined by the von Neumann model.
🌿 The Functional Programming Paradigm and Its Historical Roots
The speaker explores the functional programming paradigm, which has its roots in lambda calculus. They discuss the development of Lisp, a language created by John McCarthy that is capable of being implemented in its own language, and the subsequent rise of other functional programming languages like ML, Haskell, and Elm. The speaker connects the principles of functional programming to the constraints and benefits of the lambda calculus, and how these principles have influenced modern software development practices.
🔄 The Interplay Between Theory and Practice in Computation
In the final paragraph, the speaker reflects on the relationship between theoretical models of computation and their practical implementation. They discuss the historical context of computing and the factors that contributed to the dominance of the von Neumann model over other models like lambda calculus. The speaker also addresses the difficulty of implementing functional programming concepts in hardware and the implications for the future of computing technology.
Mindmap
Keywords
💡Theory of Computation
💡Axiomatic Thinking
💡Peano Axioms
💡Turing Machine
💡Lambda Calculus
💡Axiom Tower
💡Syntactic Sugar
💡Church-Turing Thesis
💡Von Neumann Model
💡Functional Programming
💡React
Highlights
Introduction to the theory of computation with a focus on axiomatic thinking and its foundational concepts.
Explaining the concept of multiplication as a series of additions, emphasizing the redundancy of some mathematical rules.
Introduction of axioms as the minimum subset of rules necessary to describe all of mathematics.
Giuseppe Peano's contribution to defining the natural numbers and the concept of zero.
The definition of equality and the properties of natural numbers according to Peano's axioms.
The introduction of the successor function 's' as a way to generate natural numbers.
The concept of syntactic sugar and its role in simplifying mathematical expressions.
Defining addition recursively using Peano's axioms and the concept of successor.
Multiplication defined in terms of addition, showing the intrinsic relationship between these operations.
The idea of 'axiom towers' as a way to build complex mathematical structures from simple axioms.
The non-divine nature of axioms and the flexibility in choosing different starting points for mathematical systems.
The concept of symbols and rules being intrinsically linked, with examples from computing and DNA.
The philosophical claim that mathematics is discovered rather than invented, through the examination of axiom towers.
The historical context of algorithms and their evolution before the formal definition of computation.
The independent development of Turing machines, lambda calculus, and general recursive functions as models of computation.
Alan Turing's vision of reducing algorithms to their most principal forms and the concept of Turing machines.
The description of a Turing machine's components, including the infinite tape, head, and set of instructions.
The implementation of a Turing machine in the Brainfuck language and its use in computing tasks.
The concept of Turing completeness and its significance in determining the computational power of a system.
Examples of non-traditional systems that are Turing complete, such as Conway's Game of Life and Magic the Gathering.
The introduction of lambda calculus as an alternative model of computation, focusing on functions and function application.
The definition of true and false in lambda calculus and the construction of logical operations like AND.
The Y Combinator in lambda calculus, a method for creating recursion from non-recursive functions.
The Church-Turing thesis and the equivalence of Turing machines and lambda calculus in terms of computational power.
The peculiarities of lambda calculus, including the lack of global state and the use of pure functions.
The von Neumann model of computation and its influence on the design of modern computers.
The evolution of programming languages from assembly to C++, reflecting the progression of abstraction layers in computing.
The lambda calculus tower and its influence on functional programming languages like Lisp, ML, Haskell, and Elm.
The comparison between React and jQuery, drawing parallels with the differences between lambda calculus and Turing machines.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: