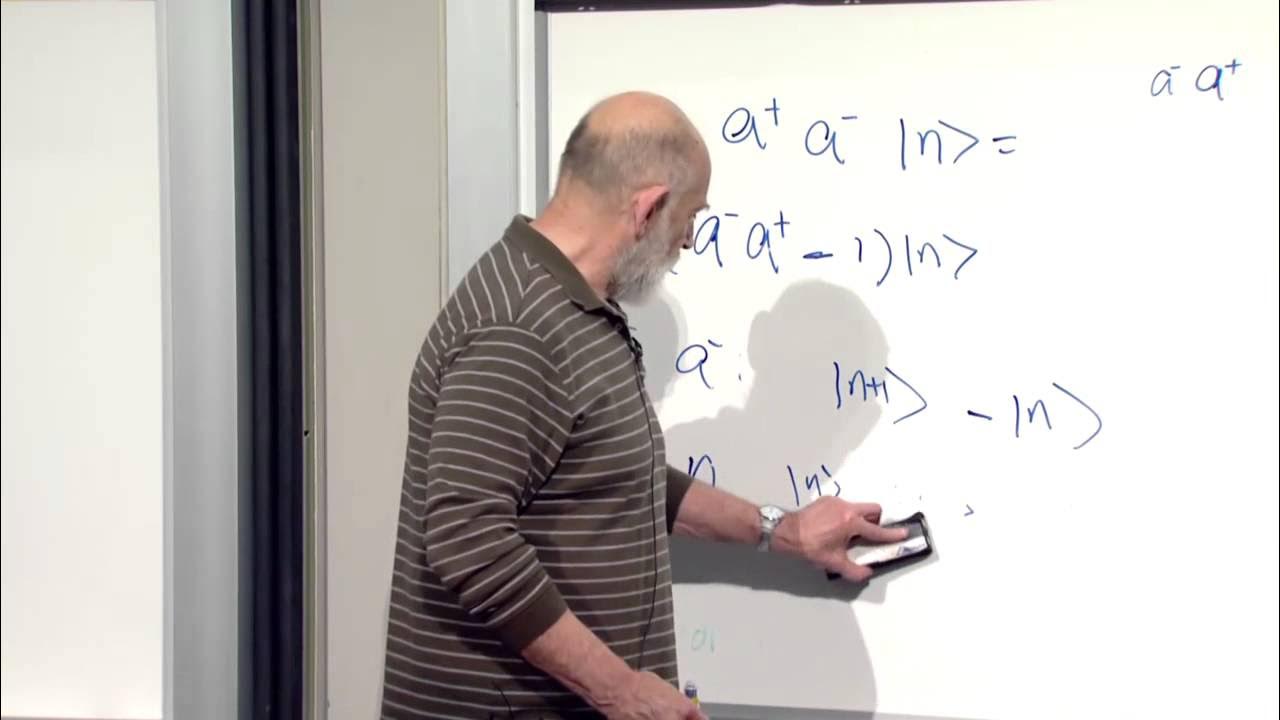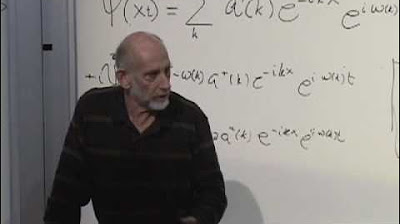Lecture 2 | New Revolutions in Particle Physics: Basic Concepts
TLDRThe video script is an educational lecture discussing the foundational concepts of quantum field theory, a fundamental tool in particle physics. The lecturer begins by emphasizing the importance of understanding quantum fields and their mathematical representation. The discussion delves into the nature of waves, their connection to particles through quantum mechanics, and the mathematical relationship between sines, cosines, and exponentials. The lecturer also explores the properties of exponential functions, the concept of fields varying throughout space, and the significance of Planck's constant in quantum mechanics. The lecture further investigates the quantization of energy in a harmonic oscillator system, touching upon the commutator properties of quantum mechanics and the role of creation and annihilation operators. These operators are integral to the manipulation of particle states in quantum field theory, allowing for the addition and subtraction of quanta of energy. The script concludes with a brief introduction to the concept of a quantum field as a collection of harmonic oscillators, setting the stage for further exploration into particle physics and quantum field theory.
Takeaways
- 📐 **Quantum Field Theory Basics**: The lecture introduces quantum field theory as a fundamental tool in particle physics, emphasizing the importance of understanding quantum fields and their relation to particles.
- 🌱 **Waves and Fields**: Waves are used as an introductory example of fields, which are configurations varying throughout space, highlighting the connection between waves, particles, and quantum mechanics.
- 🔢 **Mathematical Review**: A mathematical review of exponential functions, sines, cosines, and their derivatives is provided, setting the stage for more complex quantum mechanical concepts.
- 🌀 **Wave-Particle Duality**: The connection between waves and particles is discussed, noting that quantum mechanics is necessary for a complete understanding of this duality.
- 📉 **Special Relativity and Quantum Mechanics**: The lecturer clarifies that while special relativity is important, the focus is on quantum mechanics, which is the starting point for particle physics.
- 🌟 **Planck's Constant**: Planck's constant and its role in quantum mechanics are introduced, noting its small value and significance in the energy calculations of single photons.
- 🚀 **Momentum and Energy**: The concepts of momentum and energy are discussed in the context of non-relativistic and relativistic particles, with specific formulas provided for each case.
- 🔴 **Quantization of Momentum**: The idea that momentum is quantized in a periodic space is explored, leading to the conclusion that the momentum of any quantum is an integer multiple of a basic unit.
- 🔄 **Harmonic Oscillators**: The harmonic oscillator is presented as a simple quantum system with quantized energy levels, which is crucial for understanding the quantization of energy in quantum fields.
- 🤝 **Commutators in Quantum Mechanics**: The non-commutativity of certain quantum mechanical operators is explained, which implies that certain pairs of properties cannot be simultaneously measured with infinite precision.
- ⚙️ **Creation and Annihilation Operators**: These operators are introduced as mathematical tools that add or remove quanta of energy from oscillators, which is key for the quantum field theory and particle interactions.
Q & A
What is the basic tool of the trade in quantum field theory?
-The basic tool of the trade in quantum field theory is quantum mechanics, specifically quantum field theory itself, which describes how fields vary throughout space and how they are connected to particles through the principles of quantum mechanics.
What is the relationship between waves and fields?
-Waves are a particular kind of field configuration where the fields are moving in a wave-like motion. They are examples of fields that vary throughout space and are closely connected to particles through quantum mechanics.
How are sines and cosines related to exponential functions?
-Sines and cosines can be combined to form an exponential function involving an imaginary number. Specifically, the function cosine(KX) + I sine(KX) is equivalent to e^(iKX), where I is the imaginary unit and K is a real number. Differentiating this function with respect to X yields I K times the same function, demonstrating the relationship.
What is the significance of the Planck's constant in quantum mechanics?
-Planck's constant is a fundamental constant in quantum mechanics that relates the energy of a photon to its frequency. It is used in the equation E = h * frequency, where E is the energy of a single quantum (or photon), h is Planck's constant, and frequency is the frequency of the associated wave.
How is the momentum of a single photon related to its wavelength?
-The momentum of a single photon is inversely proportional to its wavelength. Specifically, the magnitude of the momentum (p) is given by the formula p = h / λ, where h is Planck's constant and λ is the wavelength of the photon.
What is the role of the harmonic oscillator in quantum field theory?
-The harmonic oscillator is central to quantum field theory because it represents the simplest kind of oscillation. It is used as a model to understand how energy is quantized in quantum systems, and the concept of creation and annihilation operators, which add and subtract quanta of energy, are derived from the mathematics of the harmonic oscillator.
Why is it important to consider a finite space in quantum mechanics and quantum field theory?
-Considering a finite space is important because it allows for the removal of infinities, which are problematic in physics and mathematics. By defining space as finite, such as on a circle, it becomes possible to apply the principles of quantum mechanics and quantum field theory in a way that computers can solve, which is essential for practical calculations and predictions.
What is the concept of quantization of momentum in a periodic space?
-In a periodic space, the momentum of any quantum object is quantized, meaning it can only take on discrete values. This is because the wavelength of the wave associated with the quantum object must fit into the space an integer number of times, leading to quantized values of momentum given by h / L, where h is Planck's constant and L is the total distance around the space.
How does the concept of a quantum field relate to particles?
-A quantum field is a collection of harmonic oscillators, each corresponding to a different mode of oscillation or frequency. In particle physics, particles are described as excitations or quanta of these fields. Creation and annihilation operators are used to add or remove particles (quanta) from the field, which corresponds to the process of particles being created or destroyed in physical interactions.
What is the difference between the group velocity and phase velocity of a wave packet?
-The group velocity is the speed at which the overall wave packet moves, while the phase velocity is the speed at which individual wave crests or troughs move through the packet. Generally, the group velocity is slower than the phase velocity, and it is the group velocity that corresponds to the actual velocity of a particle in non-relativistic quantum mechanics.
Why is the harmonic oscillator considered the simplest quantum system?
-The harmonic oscillator is considered the simplest quantum system because it involves oscillations, which are fundamental to understanding wave-like behavior in quantum mechanics. Its energy levels are quantized and follow a simple mathematical pattern, making it an ideal model for introducing and understanding more complex quantum systems and quantum field theory.
Outlines
📚 Introduction to Quantum Field Theory
The speaker begins by introducing the basic tool of particle physics, quantum field theory, and its relation to waves and fields. A review of mathematical fundamentals related to waves, including the connection between sines, cosines, and exponentials, is provided. The importance of quantum mechanics and special relativity as foundational knowledge is emphasized, with a focus on the mathematical relationship between frequency, wavelength, and the speed of light, particularly for light waves.
🔗 Waves, Particles, and Quantum Mechanics
The paragraph delves into the relationship between waves and particles through quantum mechanics. It discusses the mathematical fact that connects sines and cosines to exponential functions, highlighting the differentiation of these functions. The concept of wave-like oscillations and their description through functions such as sines and cosines is explored, along with the frequency and wavelength of waves and how they relate to the speed of light.
🚀 Quantum Mechanics and Planck's Constant
The discussion moves towards the equations of quantum mechanics, emphasizing Planck's constant and its role in relating wave-like motions to particles. The distinction between the rest mass of an object and the energy of a photon is highlighted, with an explanation of how the energy of a single photon is calculated. The concept of momentum in the context of electromagnetic radiation is introduced, differentiating between non-relativistic and relativistic scenarios.
🌌 Momentum and Energy of Photons
This section focuses on the momentum of a single photon, explaining how it can be derived from the energy of the photon. The relationship between the momentum, frequency, and wavelength of a photon is explored, with an emphasis on the quantization of momentum in a periodic or circular system. The significance of Planck's constant in determining the allowable momenta for particles such as photons and electrons is discussed.
🌟 Quantum Fields and Particle Creation
The speaker introduces the concept of a quantum field, explaining how it is related to particles and their quanta. The idea of creation and annihilation operators, which are fundamental to quantum field theory, is presented. The paragraph discusses how these operators allow for the addition and subtraction of energy quanta, which corresponds to the creation and annihilation of particles in particle physics experiments.
🧲 Harmonic Oscillators and Quantum Fields
The final paragraph ties together the concepts of harmonic oscillators and quantum fields. It describes how a system of waves can be thought of as a collection of harmonic oscillators, each with its own quantized energy levels. The state of such a system is characterized by the number of quanta in each mode of oscillation, and the quantum field is represented as a collection of these oscillators. The mathematical framework of quantum field theory is outlined, emphasizing the importance of understanding the harmonic oscillator as a foundation for more complex systems.
Mindmap
Keywords
💡Quantum Field Theory
💡Wave-Particle Duality
💡Exponential Functions
💡Sine and Cosine Functions
💡Angular Frequency
💡Planck's Constant
💡Momentum
💡Harmonic Oscillator
💡Quantization
💡Commutator
💡Annihilation and Creation Operators
Highlights
Quantum field theory is introduced as the fundamental tool for understanding particle physics.
Waves are used as an example of fields, which vary throughout space and are closely connected to particles through quantum mechanics.
The relationship between sines, cosines, and exponentials is emphasized as a mathematical fact of great importance in the field.
The concept of angular frequency (Omega) and its relation to frequency (F) is discussed, with Omega being equal to 2*pi*F.
The connection between the speed of light, wavelength, and frequency for light waves is reviewed, with the formula lambda = c/f.
Planck's constant and its role in quantum mechanics are introduced, with a focus on the energy of a single photon.
The momentum of a photon is derived, showing that it is proportional to the frequency of the photon and inversely proportional to its wavelength.
The concept of quantization of momentum in a periodic space is introduced, leading to the idea that momentum only comes in discrete multiples.
The harmonic oscillator is used as an analogy to describe the quantization of energy in quantum mechanical systems.
The creation and annihilation operators are introduced as mathematical tools to add and subtract quanta of energy in quantum systems.
The non-commutativity of position and momentum operators is explained, reflecting the Heisenberg uncertainty principle.
The idea that a quantum field can be thought of as a collection of harmonic oscillators, each with its own frequency, is presented.
The importance of understanding the mathematics of linear operators for grasping the concepts of quantum field theory is emphasized.
The concept of a quantum field is related to the idea of particles and their creation or annihilation in particle physics experiments.
The transcript provides a foundational understanding of quantum mechanics principles necessary for further study in quantum field theory and particle physics.
The importance of the harmonic oscillator model in understanding the behavior of particles and fields in quantum mechanics is highlighted.
The lecture concludes with a teaser for the next session, where the first example of a quantum field will be discussed.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: