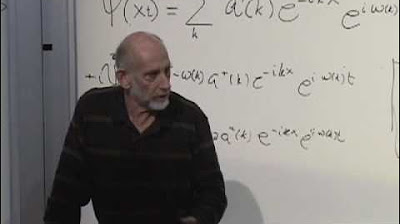Advanced Quantum Mechanics Lecture 9
TLDRThe provided video script is a detailed lecture on quantum field theory, focusing on the Hamiltonian operator within the context of particle physics. The lecturer delves into the intricacies of quantum fields, discussing creation and annihilation operators, and the Hamiltonian for a simple quantum field satisfying the Schrödinger equation. The concept of momentum conservation is explored, emphasizing the role of the Hamiltonian in updating the state of a system and how it relates to the conservation of momentum in particle interactions. The lecture also touches on the Klein-Gordon equation and Dirac's equation, providing insights into the relativistic treatment of electrons and the challenges of negative energy solutions. The discussion is both mathematically rigorous and conceptually rich, aiming to impart a deeper understanding of the foundational principles of quantum mechanics and field theory.
Takeaways
- 📐 The Hamiltonian operator for quantum fields describes the total energy of a system and is used to update the state of the system over time.
- ⚙️ Creation and annihilation operators are fundamental to quantum field theory, where they correspond to adding or removing particles from a quantum state.
- 🚀 The Schrödinger equation is central to quantum mechanics, describing how the quantum state of a physical system changes with time.
- 🌌 Momentum conservation in quantum field theory is ensured by the Hamiltonian acting on a state of definite momentum without changing it.
- 🔄 Integration over space in the Hamiltonian leads to a delta function, which is crucial for momentum conservation in interactions between particles.
- 🤹 The Hamiltonian can include various terms that represent different types of interactions, such as scattering or decay, which are determined by experimental physics.
- 🧲 Coupling constants, which can be very small or large, quantify the strength of interactions between particles in the Hamiltonian.
- ✨ The Dirac equation, a relativistic wave equation, was developed to describe particles like electrons that move at speeds close to the speed of light.
- ⚛️ The Dirac equation introduces the concept of antiparticles, which are particles with the same mass but opposite charge as their corresponding particles.
- 🧬 The theory of beta decay, involving a neutron decaying into a proton, an electron, and a neutrino, is an example of how quantum field theory can explain particle interactions.
- 🤝 The Hamiltonian in quantum field theory often includes kinetic energy terms and interaction terms that are derived from experimental observations of particle behavior.
Q & A
What is the Hamiltonian operator in the context of quantum fields?
-The Hamiltonian operator in quantum fields is used to describe the total energy of the system. It typically includes the kinetic energy of particles, potential energy, and interaction terms that dictate how particles within the field can create or annihilate one another.
How does the Hamiltonian operator update the state of a quantum system?
-The Hamiltonian operator updates the state of a quantum system by acting on the state vector to produce an evolved state over time. This is in accordance with the time-dependent Schrödinger equation, where the time derivative of the state vector is equal to the Hamiltonian operator multiplied by the state vector.
What does it mean for momentum to be conserved in a quantum system?
-Momentum conservation in a quantum system means that if the Hamiltonian operator acts on a state with a definite total momentum, it will not change the momentum of the system. The total momentum before and after the action of the Hamiltonian remains the same, even though other properties of the system may change.
What is the significance of the Dirac equation in the context of the Hamiltonian?
-The Dirac equation is a relativistic wave equation that describes particles, such as electrons, that move at speeds close to the speed of light. It is significant in the context of the Hamiltonian because it ensures that the energy-momentum relationship is consistent with the principles of special relativity, and it introduces the concept of antiparticles and negative energy solutions.
How does the creation operator in quantum field theory work?
-The creation operator in quantum field theory is used to add a particle to a quantum state. It operates on the state vector to increase the number of particles by one, creating a new state with one more particle than the original state.
What is the role of the annihilation operator in quantum field theory?
-The annihilation operator is used to remove a particle from a quantum state. When it acts on a state vector, it decreases the number of particles by one, resulting in a new state with one less particle.
How does the Hamiltonian operator account for potential energy in quantum field theory?
-The Hamiltonian operator accounts for potential energy by including terms that represent the potential energy of the particles within the field. These terms often depend on the position and can include interactions with other particles or fields.
What is the concept of a 'coupling constant' in quantum field theory?
-The coupling constant in quantum field theory is a parameter that measures the strength of an interaction between particles. It multiplies the interaction terms in the Hamiltonian and determines the probability of a particular interaction occurring.
What is the significance of the term 'momentum conservation' in quantum field theory?
-Momentum conservation is a fundamental principle in quantum field theory that ensures the total momentum of a system remains constant if no external forces are applied. This principle is crucial for ensuring the physical validity of the theory and is often manifested in the form of delta functions in the Hamiltonian.
What does the Hamiltonian operator represent in the context of quantum field theory?
-In quantum field theory, the Hamiltonian operator represents the total energy of the system. It is used to calculate the time evolution of the quantum state of the system and includes terms that describe the creation and annihilation of particles, as well as their interactions.
How does the Hamiltonian operator ensure energy conservation in quantum field theory?
-The Hamiltonian operator ensures energy conservation in quantum field theory by governing the time evolution of the system's state. Since the Hamiltonian represents the total energy, its hermitian nature guarantees that the expectation value of the energy remains constant over time, in the absence of external interactions.
Outlines
📚 Introduction to Quantum Fields and Hamiltonian Operators
The first paragraph introduces the concepts of quantum fields, creation and annihilation operators, and the Hamiltonian operator. It discusses how these operators are used to describe particles that satisfy the Schrödinger equation. The Hamiltonian for a simple quantum field is presented, incorporating position, creation and annihilation operators, mass, and potential energy. The paragraph also touches on energy conservation and momentum in the context of a quantum system.
🚀 Role of the Hamiltonian in State Updates and Momentum Conservation
The second paragraph delves into the role of the Hamiltonian in updating the state of a quantum system over time, emphasizing its importance in the Schrödinger equation. It explores the concept of momentum conservation, explaining that the Hamiltonian must not change the momentum of a system when acting on a state of definite momentum. The paragraph also discusses the process of rewriting the Hamiltonian in the momentum basis to check for momentum conservation.
🧮 Mathematical Treatment of Momentum in Quantum Systems
The third paragraph focuses on the mathematical treatment of momentum in quantum systems. It describes how the annihilation and creation operators act on states with specific momenta and how the integral over position transforms these operators into a delta function, signifying momentum conservation. The paragraph also illustrates the process of integrating over momentum variables to analyze the system's behavior.
🤔 Momentum Conservation in More Complex Hamiltonians
The fourth paragraph expands on the concept of momentum conservation when dealing with more complex Hamiltonians involving multiple fields and particles. It discusses the implications of including various creation and annihilation operators in the Hamiltonian and how the integration over space leads to a delta function that ensures the total momentum is conserved.
🔄 Exploring the Impact of Additional Derivatives in the Hamiltonian
The fifth paragraph investigates the impact of including additional derivatives in the Hamiltonian on momentum conservation. It demonstrates how the second derivative with respect to position affects the momentum of particles and how the Hamiltonian, through its interaction with the quantum field, accounts for the kinetic energy of particles.
🤝 Interactions and Scattering in Quantum Field Theory
The sixth paragraph discusses the representation of interactions and scattering processes in quantum field theory through the Hamiltonian. It provides an example of a simple interaction between two types of particles, highlighting how the Hamiltonian can describe scattering processes and the importance of momentum conservation in these interactions.
🧲 Coupling Constants and Their Role in Quantum Field Theory
The seventh paragraph introduces the concept of coupling constants in the Hamiltonian, which quantify the strength of interactions between particles. It explains how these constants can be determined experimentally and how they influence the probability of interactions occurring. The paragraph also touches on the idea of different types of symmetries in quantum field theory.
🌀 The Dirac Equation and Its Significance in Quantum Mechanics
The eighth paragraph presents the Dirac equation, a fundamental equation in quantum mechanics that describes relativistic electrons. It discusses the equation's derivation, its relation to the Schrödinger equation, and the importance of incorporating relativistic effects for a more accurate description of electron behavior in atoms.
🔍 Dirac's Approach to Relativistic Quantum Mechanics
The ninth paragraph explores Dirac's approach to formulating a relativistic version of the Schrödinger equation. It contrasts the Dirac equation with the Klein-Gordon equation and explains Dirac's reasoning for preferring a first-order differential equation involving the Hamiltonian. The paragraph also highlights the challenges Dirac faced in finding a suitable operator for the square root of the momentum operator.
🚦 Introducing the Dirac Matrix and Its Role in Describing Particle Degrees of Freedom
The tenth paragraph introduces the Dirac matrix, which is used to describe the degrees of freedom of a particle, specifically its momentum and 'handedness' or chirality. It explains how the Dirac matrix allows for the description of particles moving in both directions and how it incorporates the mass of the electron into the equation.
🔗 The Dirac Equation and the Incorporation of Mass
The eleventh paragraph discusses how the Dirac equation accommodates the mass of the electron, allowing for a description of particles that move slower than the speed of light. It explains the coupling of the two components of the wave function due to the mass term and how this coupling gives the particle a mass and makes it a relativistic particle of finite mass.
🔬 Factorization and the Dirac Equation in Three Dimensions
The twelfth paragraph addresses the factorization of the Dirac equation and its extension to three dimensions. It mentions the need to move beyond the one-dimensional case to fully capture the behavior of electrons and hints at the complexities involved in the three-dimensional Dirac equation.
📝 Conclusion and Further Exploration of the Dirac Equation
The final paragraph summarizes the discussion on the Dirac equation and its implications for quantum mechanics. It acknowledges the complexity of the equation and its significance in understanding the behavior of relativistic electrons. The paragraph also suggests that further exploration of the Dirac equation and its various forms will be continued in subsequent discussions.
Mindmap
Keywords
💡Quantum Fields
💡Creation and Annihilation Operators
💡Hamiltonian Operator
💡Schrodinger Equation
💡Momentum Conservation
💡Potential Energy
💡Kinetic Energy
💡Dirac Equation
💡Lorentz Transformation
💡Chirality
💡Coupling Constant
Highlights
Discussion on Quantum Fields, creation and annihilation operators, and the Hamiltonian operator for a simple Quantum Field.
Explanation of how the Hamiltonian operator updates the state of a system and its role in energy and momentum conservation.
Derivation and significance of the Hamiltonian for a system of particles in a potential, and the concept of potential energy.
Introduction of a constant potential energy term in the Hamiltonian and its implications on particle energy.
Use of the Schrödinger equation to describe how the Hamiltonian changes the state of a system over time.
Momentum conservation principle and its verification through the Hamiltonian operator.
Rewriting of the annihilation and creation operators in the momentum basis and the use of Fourier transforms.
Integration over position leading to a Delta function and its importance in momentum conservation.
Generalization of the Hamiltonian to include multiple fields and particles, leading to more complex interactions.
Inclusion of derivatives in the Hamiltonian and their effect on momentum and kinetic energy.
Example of an interaction term in the Hamiltonian that represents scattering between two species of particles.
Discussion on the Dirac equation, its formulation, and the inclusion of the mass term to describe particles with mass.
Introduction of the Dirac 'alpha' and 'beta' matrices and their role in the Dirac equation.
Solution to the problem of negative energy solutions in the Dirac equation through the concept of antiparticles.
Transformation to three-dimensional space and its implications for the Dirac equation.
Explanation of the chirality or handedness in the context of the Dirac equation and its relation to particle mass.
Discussion on the experimental input of coupling constants in Quantum Field Theory and their role in particle interactions.
Introduction to Feynman diagrams and their use in visualizing and calculating interactions in Quantum Field Theory.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: