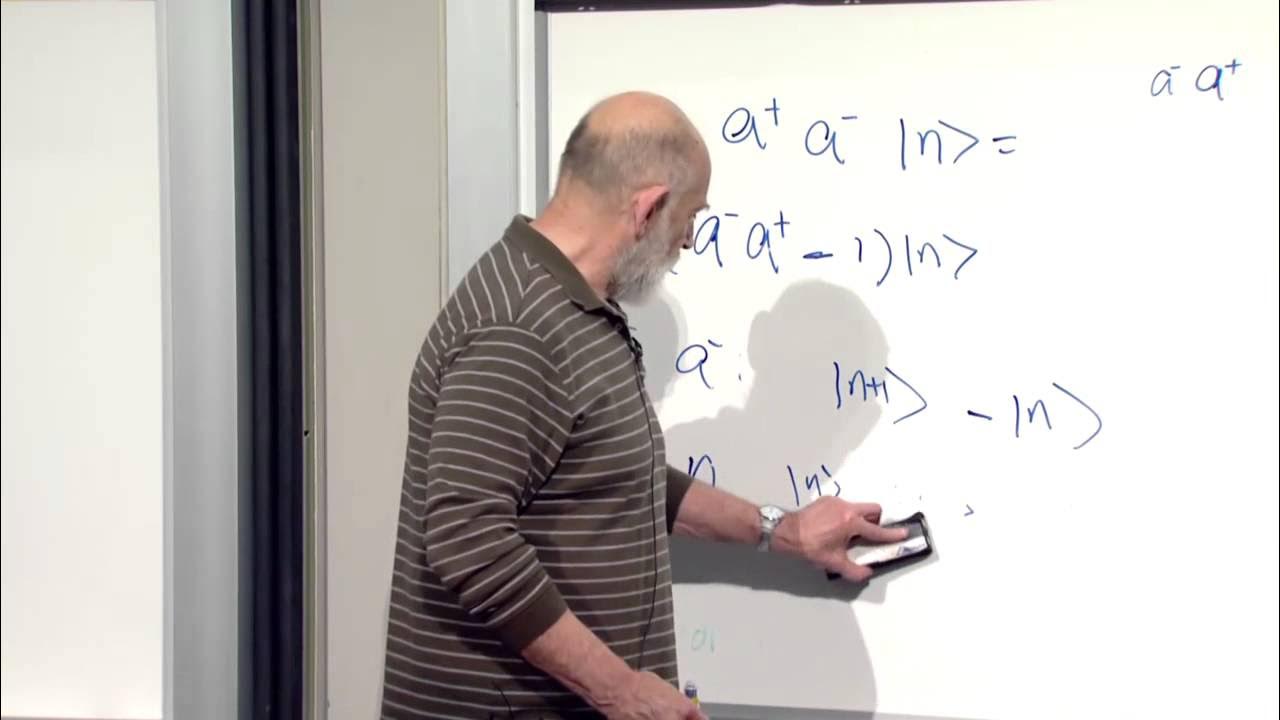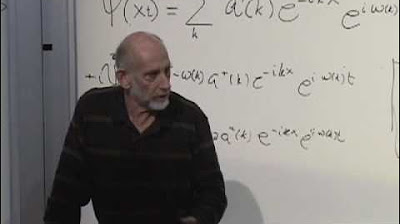Lecture 3 | New Revolutions in Particle Physics: Basic Concepts
TLDRThe video script delves into the fundamental concept of quantum fields, illustrating how they relate to particles and the role of harmonic oscillators in their mathematical formulation. It explains the use of periodic spaces, like a circle, to maintain momentum conservation and the significance of quantized wave numbers. The script explores the relationship between wave number and wavelength, and their connection to momentum. It further discusses the concept of occupation numbers, which represent the number of quanta or particles with a given wave number or momentum. The video introduces quantum mechanical operators, such as creation and annihilation operators, and their role in changing the number of particles in a system. It also touches on the Fourier decomposition of quantum fields and how these fields can be used to describe particle interactions, including scattering processes and particle creation or annihilation. The script concludes with a discussion on the behavior of bosons and fermions in quantum field theory, highlighting the difference in their algebraic properties and the implications for particle interactions and the possibility of stimulated emission.
Takeaways
- 🚀 The concept of a quantum field is central to quantum mechanics, relating to particles and described using harmonic oscillators.
- 🌀 Quantum fields can be represented on a periodic space, which simplifies the mathematics and allows for the conservation of momentum.
- 🔬 The wave number 'K' in quantum fields is quantized and related to the momentum of particles, with Planck's constant serving as a conversion factor.
- 🌊 A plane wave on a circle, representing a quantum field, can be decomposed into Fourier components, which are analogous to creation and annihilation operators.
- 📓 The occupation number 'n' represents the number of quanta or particles with a given wave number 'K', which is crucial for describing the state of a quantum field.
- 🤹♂️ Quantum field operators, such as 'a plus of K' and 'a minus of K', allow for the manipulation of particle states, including creation and annihilation processes.
- 🧲 The quantum field operator 'ψ' can be thought of as a Fourier series with coefficients that are quantum mechanical operators, which can create or annihilate particles at specific positions.
- ✨ The probability of particle creation in quantum fields can be influenced by the presence of other particles, a phenomenon exemplified by stimulated emission in the context of photons.
- ⚛️ Bosons, a type of quantum particle, are characterized by their ability to occupy the same quantum state, which is reflected in the commutation relations of their creation and annihilation operators.
- 📈 The number of particles in a quantum field can be observed and is related to the integral of the quantum field operator squared over space.
- 📊 Quantum fields behave classically when the number of quanta is large, adhering to the uncertainty principle and allowing for approximate simultaneous measurement of field components.
Q & A
What is a quantum field?
-A quantum field is a field that is quantized, meaning it is subject to the principles of quantum mechanics. It is related to particles and is described using the mathematical framework of quantum field theory, which allows for the creation and annihilation of particles.
Why are harmonic oscillators important in quantum fields?
-Harmonic oscillators are important in quantum fields because they provide the basic mathematical tool for describing quantum fields. They help in understanding how oscillators together can make quantum fields, especially in the context of periodic spaces.
What is the significance of a periodic space in quantum field theory?
-A periodic space is significant because it allows for the existence of waves that can move in one direction without reflecting, which is essential for maintaining momentum conservation. This is particularly useful when dealing with finite systems where infinite volumes are not a concern.
How is the wave number (K) related to momentum in quantum field theory?
-In quantum field theory, the wave number (K) is directly related to the momentum (P) of a particle. The relationship is given by P = ħK, where ħ is the reduced Planck constant. This shows that the momentum of a particle is proportional to its wave number.
What are occupation numbers in the context of quantum fields?
-Occupation numbers in quantum fields represent the number of quanta or particles with a given wave number (K) or momentum (P). They are used to describe the number of particles occupying a particular quantum state with a specific momentum.
What is the role of creation and annihilation operators in quantum field theory?
-Creation and annihilation operators are used to describe changes in the number of particles in a quantum field. The creation operator (a†) increases the number of particles in a state by one, while the annihilation operator (a) decreases it by one. These operators are crucial for describing processes such as particle scattering and creation.
How does the concept of a quantum field differ from that of a classical field?
-A classical field, such as the electromagnetic field, is continuous and deterministic, whereas a quantum field is discrete and probabilistic. Quantum fields allow for the creation and annihilation of particles, which is not possible in classical fields. Additionally, quantum fields are subject to the uncertainty principle, which is not a factor in classical physics.
What is the connection between the Fourier coefficients and the creation and annihilation operators in quantum field theory?
-The creation and annihilation operators (a† and a) in quantum field theory are the quantum mechanical versions of the Fourier coefficients. They represent the amplitudes of the Fourier components of the field, and their real and imaginary parts correspond to observable quantities in the theory.
How does the concept of a quantum field apply to the description of particle reactions?
-Quantum fields allow for the description of particle reactions by using creation and annihilation operators to represent the processes where particles are created or destroyed. For example, a reaction where one particle comes in and two particles go out can be described using these operators to show changes in the number of particles.
What is the significance of the commutation relations in quantum field theory?
-Commutation relations are crucial in quantum field theory as they define the algebraic properties of the creation and annihilation operators. These relations ensure that the operators follow the correct rules when acting on quantum states, which is essential for the consistent mathematical formulation of the theory.
How does the concept of a vacuum state relate to quantum field theory?
-In quantum field theory, the vacuum state is the state with no particles present. It is also the ground state and the state of lowest energy. The vacuum state plays a fundamental role in the theory as it is the starting point for describing processes such as particle creation and annihilation.
Outlines
📐 Introduction to Quantum Fields and Harmonic Oscillators
The paragraph introduces the concept of a quantum field, relating it to particles and harmonic oscillators. It explains how quantum fields are mathematically represented using harmonic oscillators and the significance of a periodic space for maintaining momentum conservation. The role of wave numbers and their quantization in creating quantum fields is also discussed.
🌌 Wave Number, Wavelength, and Momentum Relationships
This section delves into the relationship between wave numbers, wavelengths, and momentum. It establishes that the wave number is quantized and relates it to the quantization of wavelength. The connection between the wave number (K) and momentum (P) is explored, highlighting their proportionality through the Planck constant (h-bar).
🚀 Occupation Numbers and Quantum Mechanical Operators
The paragraph discusses occupation numbers, which represent the number of quanta with a specific wave number or momentum. It introduces quantum mechanical operators, which act on state vectors to describe the system's observables. The concept of a quantum state for a system of quanta moving on a circle is also introduced.
🔄 Raising and Lowering Operators and Quantum Field Construction
The discussion moves to raising and lowering operators, which are analogous to the creation and annihilation operators in quantum field theory. These operators are used to describe the changes in the number of quanta with a given momentum. The paragraph also explains how quantum fields are constructed using these operators.
🤔 Fourier Coefficients and Quantum Field Representation
This section explores the representation of a quantum field as a Fourier series, where the Fourier coefficients are represented by creation and annihilation operators. It discusses the transition from discrete to continuous values of momentum and how this is reflected in the quantum field's representation.
💡 Particle Creation, Annihilation, and Scattering Processes
The paragraph covers how quantum field theory allows for the description of particle creation, annihilation, and scattering processes. It provides examples of how these processes can be represented using the creation and annihilation operators and discusses the importance of maintaining locality in quantum field interactions.
🌟 Photon Interactions and Particle Production Probabilities
This section focuses on the interaction of photons, particularly the process where a single photon is absorbed and results in the emission of two photons. The concept of indistinguishable particles and the role of the square root of the number of particles in determining probabilities are explained.
🎓 Bosons and Fermions: Creation and Annihilation Operators
The paragraph distinguishes between bosons and fermions, highlighting their different properties and behaviors. It explains the mathematical rules governing the creation and annihilation operators for bosons and how these particles tend to occupy the same state, a concept known as stimulated emission.
🧲 Measuring Quantum Fields and the Role of Uncertainty
The discussion addresses the challenge of measuring quantum fields due to the non-commutativity of their components. It explains that while fields cannot be precisely measured simultaneously, their components can be approximately measured without violating the uncertainty principle, especially when the number of quanta is large.
🔍 Quantum Field Theory in Practice and External Fields
This section touches on the practical application of quantum field theory, including the use of cavities with reflecting walls as a common situation for field application. It also briefly mentions the concept of external fields and their role in quantum field interactions.
🧬 Fermions and the Pauli Exclusion Principle
The final paragraph contrasts fermions with bosons, emphasizing that fermions obey the Pauli exclusion principle, meaning no two fermions can occupy the same quantum state. The algebra of fermionic creation and annihilation operators reflects this principle, and the paragraph hints at the possibility of creating bosons from fermions.
Mindmap
Keywords
💡Quantum Field
💡Harmonic Oscillator
💡Momentum Conservation
💡Wave Number
💡Occupation Number
💡Quantum Mechanical Operators
💡Fourier Coefficients
💡Particle Scattering
💡Vacuum State
💡Indistinguishable Particles
💡Stimulated Emission
Highlights
Introduction to the concept of a quantum field and its relation to particles, emphasizing the importance of harmonic oscillators.
Explanation of how periodic space can maintain momentum conservation, which is crucial for quantum field theory.
Discussion on the quantization of wave numbers and their connection to momentum, a fundamental aspect of quantum mechanics.
The relationship between wavelength, wave number, and momentum is explored, highlighting the inverse nature of these quantities.
Introduction of occupation numbers as a way to describe the number of quanta with a given wave number or momentum.
Description of quantum mechanical operators and their role in changing the state of a system, crucial for observables in quantum mechanics.
The use of Fourier coefficients in quantum fields, drawing parallels between classical and quantum mechanical representations of fields.
Explanation of how quantum fields can describe particle creation and annihilation, a key breakthrough in quantum field theory.
The role of the quantum field ψ(X) as a creation operator for a particle at a specific position, a fundamental concept in quantum field theory.
Discussion on the probability amplitudes in quantum mechanics and how they relate to the creation and annihilation of particles.
The concept of stimulated emission is introduced, explaining how the presence of particles can enhance the probability of certain quantum processes.
Differentiation between fermions and bosons, highlighting their distinct behaviors and implications in quantum field theory.
The algebraic properties of creation and annihilation operators for bosons, which are fundamental to understanding quantum field dynamics.
Implications of the uncertainty principle on the measurable components of quantum fields, especially when the number of quanta is large.
The behavior of quantum fields in the classical limit, where fields behave as classical wave fields under certain conditions.
The transition from a one-dimensional model to higher dimensions, such as two or three dimensions, in quantum field theory.
Speculation on the applicability of quantum field theory at different length scales, touching upon the limits of the theory.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: