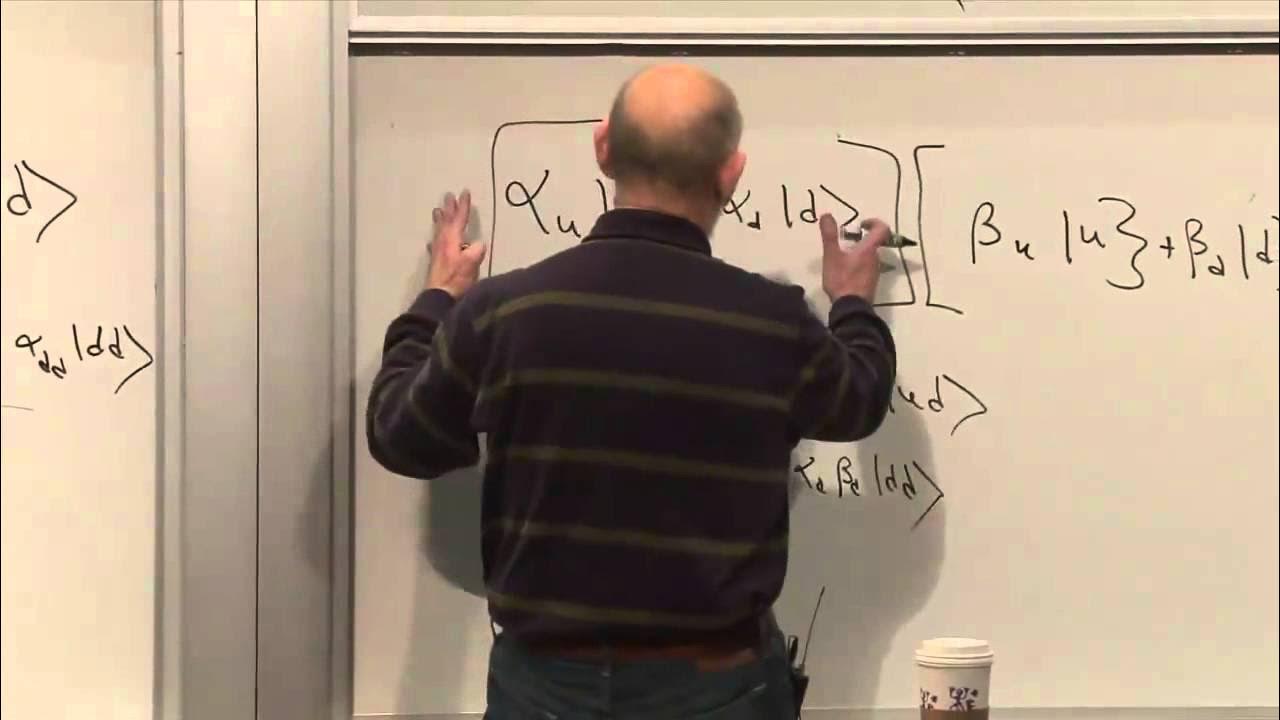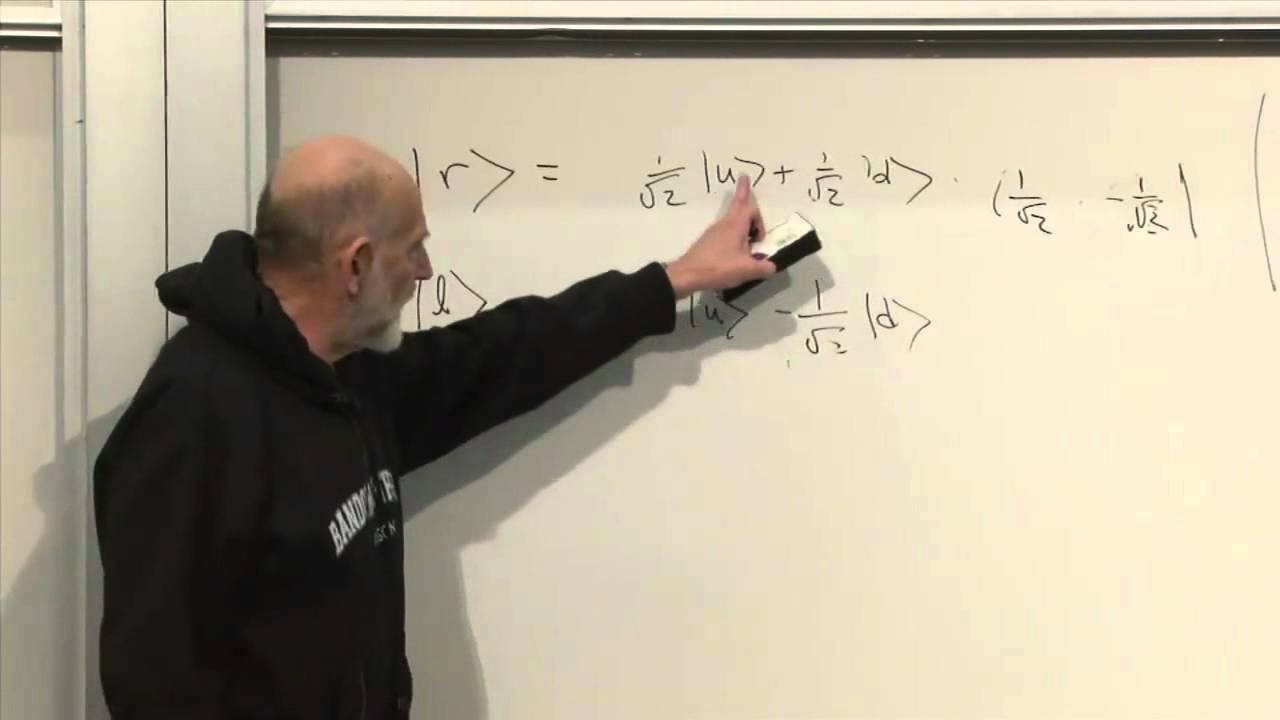Lecture 4 | Quantum Entanglements, Part 1 (Stanford)
TLDRThe video script is a detailed lecture on quantum mechanics, specifically focusing on the concept of quantum entanglement. It begins with an exploration of the quantum bit or 'qubit' system and the entanglement phenomenon associated with two electrons and their spins. The lecturer delves into the mathematics of quantum states, the use of sigma matrices to represent spin states, and the probability amplitudes in quantum measurements. The script also discusses the impossibility of measuring certain spin states simultaneously due to their non-commutative nature, a fundamental aspect of quantum theory. The concept of entangled states is introduced with the example of a 'singlet state' of two electrons, where the spin state of one electron instantly influences the state of the other, no matter the distance between them. This leads to a thought-provoking discussion on the peculiarities of quantum correlations and the potential for applications in quantum computing and communication.
Takeaways
- 📚 The script is an educational lecture discussing quantum mechanics, specifically focusing on the concept of quantum entanglement and the behavior of electron spins.
- 🌀 Entanglement involves a quantum state where two or more particles become linked, and the state of one particle is immediately connected to the state of the other, regardless of the distance between them.
- ⚛️ The simplest case of entanglement is between two electrons and their spins. The lecture delves into the quantum states that can be formed when systems have multiple parts.
- 🧲 The concept of a magnetic moment or spin vector is introduced, which is measurable and can be represented by components along the x, y, and z axes.
- 🎯 The script explores the probability amplitude and how it is used to calculate the probability of a certain outcome when measuring quantum states, which is central to quantum mechanics.
- 📏 The importance of the angle between two vectors (n and m) in determining the probability of measuring a specific spin state is highlighted, emphasizing rotational symmetry in physics.
- 🚫 It is shown that certain quantum properties, like the spin components of an electron along two different axes, cannot be simultaneously measured with precision due to the non-commutativity of certain quantum operators.
- 🤔 The script touches on the philosophical and interpretive questions raised by quantum mechanics, such as the nature of reality and the implications of entanglement for our understanding of the universe.
- 📈 The process of normalization of quantum states is explained, which is essential for ensuring that the probabilities of different outcomes sum to one, as required by the principles of quantum mechanics.
- 🔬 The lecture provides a detailed mathematical approach to finding the eigenvectors corresponding to the spin states of electrons, which is crucial for understanding entanglement.
- ⏱️ Time is mentioned as a factor in the interaction of electron beams, where the typical time scales may not be sufficient for certain quantum interactions to occur, such as the alignment of electron spins.
Q & A
What is entanglement in quantum mechanics?
-Entanglement is a quantum phenomenon where the quantum states of two or more particles become interlinked so that the state of one particle cannot be described independently of the state of the others, even when the particles are separated by a large distance.
How does the concept of a unit vector relate to quantum states in the context of electron spins?
-A unit vector is used to represent an arbitrary axis in space along which the spin component of an electron is measured. The components of this unit vector are related to the probabilities of finding the electron's spin in a particular state along that axis.
What is the significance of the sigma matrices in quantum mechanics?
-Sigma matrices, also known as Pauli matrices, are used in quantum mechanics to represent the spin operators for electrons. They are essential in describing the quantum states and transformations related to the spin of particles.
How does the dot product operation relate to measuring the spin component along an arbitrary axis?
-The dot product is used to calculate the component of the spin vector (represented by the sigma matrices) along an arbitrary axis (represented by the unit vector). It provides a means to find the measurable quantity of spin in that direction.
What is the probability amplitude in quantum mechanics, and how is it used?
-The probability amplitude is a complex number that, when squared and taken as the absolute value, gives the probability of a particular outcome in a quantum measurement. It is used to calculate the likelihood of finding a particle in a specific state after a measurement.
What is the role of the inner product in calculating probabilities in quantum mechanics?
-The inner product of two quantum state vectors (or the inner product of a state vector with itself) is used to calculate the probability of transitioning from one state to another or the probability of a system being in a particular state.
Why is it not possible to simultaneously measure the spin components of an electron along two different axes?
-It is not possible because the act of measurement disturbs the system. When you measure the spin component along one axis, the electron's spin collapses to a state along that axis, making it impossible to know the spin component along a different axis simultaneously.
What is the significance of the angle between two vectors in determining the probability of a quantum event?
-The angle between two vectors, such as the orientation of the electron's spin and the measurement axis, determines the probability of finding the electron's spin pointing in a particular direction. It is related to the cosine of the angle between the vectors and is a fundamental aspect of quantum mechanical predictions.
What is the meaning of the term 'eigenstate' in quantum mechanics?
-An eigenstate in quantum mechanics is a state of a quantum system that does not change when a measurement is made. The result of the measurement is an eigenvalue, which corresponds to a specific property of the system, such as the spin component along a certain axis.
How does the concept of normalization apply to quantum state vectors?
-Normalization of a quantum state vector ensures that the sum of the squares of the probabilities of all possible outcomes is equal to one, which corresponds to a 100% probability that the system will be found in one of the possible states upon measurement.
What is the implication of the complex conjugate in quantum mechanics calculations?
-The complex conjugate is used when calculating probabilities in quantum mechanics. When finding the probability of a quantum event, the amplitude of the probability is multiplied by its complex conjugate, which ensures that the probability is a real, non-negative number.
Outlines
😀 Introduction to Quantum Entanglement
The speaker begins by introducing the topic of quantum entanglement, which involves the peculiar correlations between particles like electrons. They mention that Bell's theorem and the concept of entanglement will be discussed later, emphasizing the complexity of understanding quantum systems with more than one part. The focus is on the simplest quantum system: the spin of a single electron, and the challenge of measuring its spin along an arbitrary axis.
🧲 Magnetic Moments and Quantum Measurement
The paragraph delves into the representation of physical quantities like magnetic moments or spin vectors as matrices. The speaker explains how these matrices operate on vectors, leading to measurable outcomes. The concept of hermitian matrices is introduced, which have real eigenvalues and is crucial for quantum observables. The speaker also discusses the properties of sigma matrices and their role in representing spin measurements.
📐 Angular Dependencies in Quantum Mechanics
The discussion shifts to the probabilities involved in measuring the spin of a particle along different axes. The speaker explores the question of finding the probability of measuring a certain spin component along one axis given that the particle was prepared along a different axis. The importance of rotational symmetry in quantum mechanics is highlighted, leading to the conclusion that the probability depends only on the angle between the two axes.
🌀 The Quantum Calculus of Probabilities
The speaker outlines the historical development of quantum mechanics, starting with Einstein's recognition of probabilities in quantum theory, through the contributions of Born, Heisenberg, and Dirac. The paragraph emphasizes that quantum mechanics is based on experimental facts and a calculus of probabilities. The process of calculating probability amplitudes and their squares to find probabilities is explained, which is central to quantum mechanics.
🎯 Quantum Measurement and State Preparation
The focus is on the process of quantum measurement and how it affects the state of a system. The speaker explains that measuring a quantum system, such as an electron's spin, changes its state. The concept of eigenstates and eigenvalues is introduced, and the importance of the inner product in quantum mechanics is discussed. The speaker also touches on the normalization of quantum states.
🤔 The Nature of Quantum States and Measurement
The speaker explores the idea that quantum mechanics allows for probabilities rather than certainties. They discuss the case where two measurement axes are perpendicular and the expected probability outcomes. The concept of a quantum state being a filter is introduced, and the impossibility of simultaneously measuring two non-commuting observables, like Sigma 1 and Sigma 2, is explained.
🔍 Exploring the Commutator and Entangled States
The discussion moves to the commutator, a mathematical tool that determines whether two observables can be simultaneously measured. The speaker presents a theorem stating that if two matrices commute, they share the same set of eigenvectors, and thus their corresponding observables can be measured at the same time. The concept of entangled states is introduced, where the state of one particle cannot be described independently of the other.
🌐 The Geometry of Quantum States
The speaker discusses the geometric interpretation of quantum states, emphasizing that any quantum state can be expressed as an eigenvector of some sigma matrix. This is demonstrated through counting equations and variables, showing that for any given state, there is always a direction in space where the electron's spin is definitely up or down. The concept of degrees of freedom in quantum states is explored.
🤓 Entanglement and the State of Two Electrons
The speaker explores the concept of entanglement further by considering a system of two electrons. They explain how the state of two electrons can be described in a four-dimensional vector space and how the spin operators for each electron act on these states. The importance of distinguishing between product states, where each electron has its own independent state, and entangled states, where the electrons are linked in a way that the state of one cannot be described without the other, is highlighted.
🔬 Creating and Understanding Entangled States
The speaker describes how to create an entangled state of two electrons where the spin of one electron is always opposite to that of the other, regardless of the direction of measurement. This state is known as the singlet state. The process involves bringing two electrons close enough for their magnetic fields to interact, leading to a state where the electrons' spins are anti-aligned. The speaker also touches on the philosophical implications of entanglement and the difference between classical and quantum correlations.
Mindmap
Keywords
💡Entanglement
💡Spin
💡Quantum Mechanics
💡Sigma Matrices
💡Probability Amplitudes
💡
💡Unit Vector
💡Eigenvalues and Eigenvectors
💡Quantum Superposition
💡Quantum Entanglement Experiment
💡Commutator
Highlights
Exploration of entanglement in quantum mechanics, focusing on the simplest case involving two electrons and their spins.
Discussion on the complexity of understanding quantum states for systems with multiple parts.
Introduction to the concept of a unit vector and its role in representing an arbitrary axis in space.
Explanation of the dot product in the context of physical vectors and measurable quantities.
Use of sigma matrices to represent spin operators and their properties in quantum mechanics.
Derivation and significance of the equation relating n plus and n minus with the components of the unit vector n.
Probing the probability amplitude in quantum mechanics and its relation to the outcome probabilities in measurements.
The experimental fact that quantum mechanics is based on a set of empirical probabilities.
Procedure to calculate the eigenvectors of sigma matrices and their importance in quantum calculations.
Understanding the concept of normalization in quantum states and its significance in physical measurements.
The revelation that the outcome of measuring the spin along one axis definitively determines the spin state along that axis.
Discussion on the impossibility of simultaneously measuring two non-commuting observables in quantum mechanics.
Introduction to the theorem that if two matrices commute, they share the same set of eigenvectors.
Explanation of the 'single spin' theorem which states that for any vector, there exists a direction in space such that the spin along that direction is definitely plus.
The theoretical and experimental methods to determine the direction of an electron's spin.
Insight into the creation of entangled states of electrons and their implications for quantum physics.
The singlet state of two electrons as an example of a quantum entangled state, where the spin of one electron is always opposite to the other.
Discussion on the practical creation of electron states through interaction with magnetic fields.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: