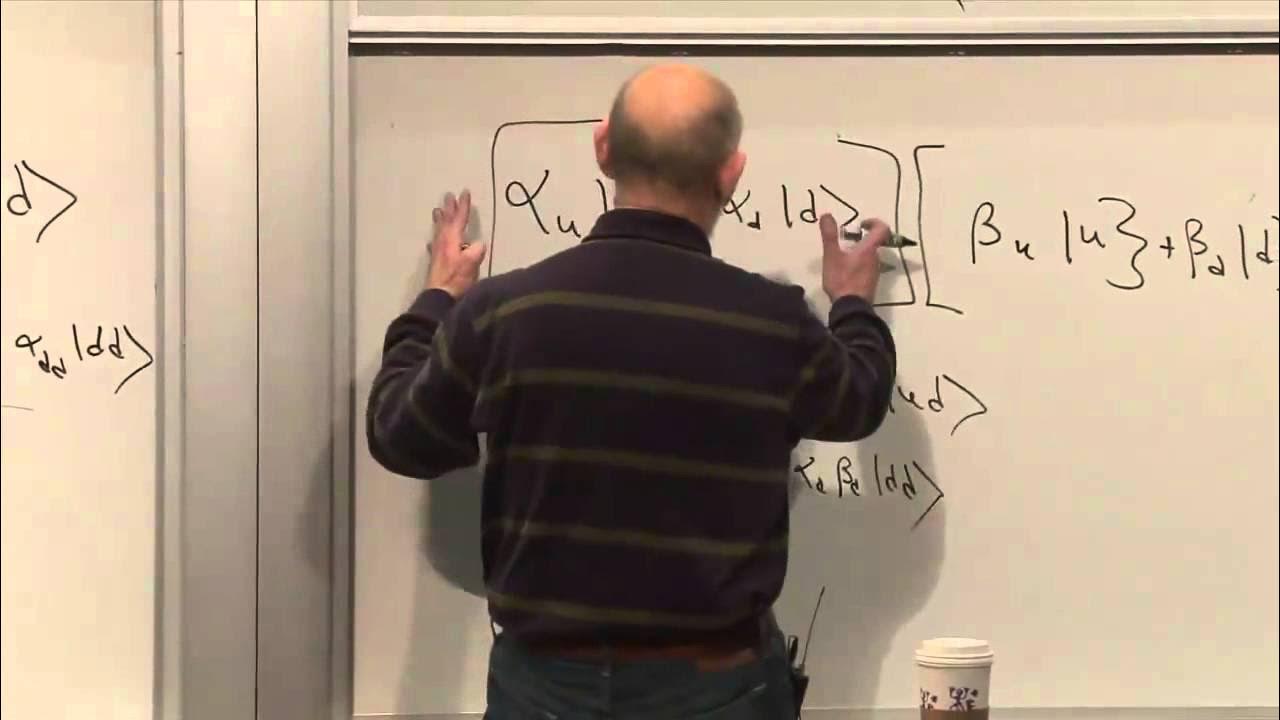Lecture 2 | The Theoretical Minimum
TLDRThe video script is an in-depth exploration of quantum mechanics, specifically focusing on the concept of a qubit, or spin, in the context of a quantum system. The lecturer introduces the idea of a 'pointer' to describe vectors in three-dimensional space and emphasizes the importance of understanding the apparatus used to measure quantum systems. The script delves into the differences between classical and quantum physics, particularly how measurements in quantum mechanics inevitably alter the system being measured. It also discusses the logic of quantum systems, which differs from classical logic, through the use of propositions and the space of states. The lecturer uses the example of a spin to illustrate how quantum states can be represented as vectors in a complex vector space, and how these states are described by their probabilities when measured along different axes. The summary also touches on the concept of orthogonality in quantum states and the significance of the dimensionality of the vector space in representing the physical states of a quantum system. The script challenges the viewer to rethink their understanding of logic and state representation, providing a foundational understanding of the mathematical framework that underlies quantum theory.
Takeaways
- 📚 The concept of a qubit is introduced as a 'spin', emphasizing its directional property in three-dimensional space.
- 🎯 Quantum mechanics differs from classical physics in that measurements in quantum systems inevitably alter the system, as opposed to classical systems where measurements can be arbitrarily gentle.
- 🧲 The 'pointer' concept is used to describe vectors in three-dimensional space, which can sometimes be referred to as 'three vectors'.
- 📊 In quantum physics, the apparatus used for measurement plays a crucial role in determining the outcome, and the orientation of the apparatus affects the result of the spin measurement.
- 🤔 The logic of quantum mechanics is distinct from classical logic, particularly in how propositions are combined using 'and' and 'or' operations.
- 📐 The space of states of a quantum system is a complex vector space, where states can be represented as vectors, and these vectors can be added and multiplied by complex numbers.
- 🌀 The inner product of a vector with itself in quantum mechanics is equivalent to the square of the length of the vector, which is always real and positive.
- 🔍 Orthogonality in quantum mechanics means that two states are physically distinguishable, and orthogonal vectors have an inner product of zero.
- 🧬 The dimensionality of a vector space is determined by the maximum number of mutually orthogonal vectors it can contain.
- 🤓 The probabilities associated with measuring a quantum state are given by the square of the magnitude of the coefficients of the state's vector in the basis of the measurement.
- 🔄 The overall phase of a quantum state does not affect its physical properties, indicating a redundancy in the description of the state.
Q & A
What is the basic difference between measurements in classical physics and quantum physics?
-In classical physics, measurements can be arbitrarily gentle, meaning you can learn anything about a system without significantly affecting it. In quantum physics, measurements inevitably change the system; you cannot measure something without affecting something else.
What does the term 'pointer' refer to in the context of this transcript?
-The term 'pointer' is used to refer to vectors in three-dimensional space. It was considered awkward and later replaced by the term 'three vectors' in the transcript.
How does the apparatus measure the spin in different directions?
-The apparatus measures the spin by aligning itself with a particular direction and interacting with the spin. The result, either plus one or minus one, corresponds to the component of the spin along the direction the apparatus is pointing.
What is the significance of the term 'reproducibility' in quantum mechanics?
-Reproducibility in quantum mechanics refers to the ability to get the same measurement result when measuring the same property of a quantum system multiple times in a row with the same apparatus.
Why does the average value of sigma x equal zero when starting with a spin up along the z-axis?
-The average value of sigma x equals zero because if you start with the spin up along the z-axis and then measure it along the x-axis, you have an equal probability of getting plus one or minus one, and their average cancels out to zero.
How does the concept of 'state' in quantum mechanics relate to the logic of classical physics?
-The concept of 'state' in quantum mechanics is different from the logic of classical physics. Quantum states form a set of possible states, and propositions about these states are subsets of these states for which the proposition is true. However, the operations of combining these propositions through 'and' and 'or' are different in quantum mechanics.
What is the role of the Pauli matrices in quantum mechanics?
-Pauli matrices are used in quantum mechanics to represent the spin states and operations on these states. They are essential in describing the quantum states of spin-1/2 particles, such as electrons.
What does it mean for two quantum states to be orthogonal?
-Two quantum states are orthogonal if their inner product is zero. This means that the states are sufficiently different that a single experiment can distinguish between them without ambiguity.
How does the concept of a vector space apply to the states of a quantum system?
-The states of a quantum system form a complex vector space. This means that any two states can be added together to create a new state, and each state can be multiplied by a complex number. The space of states is also a two-dimensional vector space for a single spin system.
What is the relationship between the probabilities of measuring 'up' or 'down' for a quantum state and the coefficients of its expansion in the 'up' and 'down' basis?
-The probability of measuring 'up' for a quantum state is the square of the magnitude of the coefficient of the 'up' component in its expansion. Similarly, the probability of measuring 'down' is the square of the magnitude of the 'down' component's coefficient.
Why is it not possible to find a third pair of orthogonal states in addition to 'up', 'down', 'left', and 'right' for a single spin system?
-It is not possible to find a third pair of orthogonal states because the space of states for a single spin system is two-dimensional. Each pair of orthogonal states spans the space, and adding another pair would require a higher-dimensional space.
Outlines
📚 Introduction to Quantum Mechanics and Spin States
The paragraph introduces the concept of a qubit, which is redefined as a 'spin' for simplicity. It discusses the abstract nature of vectors in quantum mechanics and the need to consider the system's interaction with measurement apparatus. The difference between classical and quantum physics is highlighted, emphasizing that quantum measurements inevitably alter the system, unlike classical physics where measurements can be made without significant disturbance.
🧲 Quantum Directionality and Apparatus Interaction
This section delves into the logic of quantum mechanics, focusing on the spin as a quantum system with directionality. It describes an apparatus that measures the spin's 'z component' and how the outcome of this measurement is either +1 or -1, regardless of the apparatus's orientation. The paragraph also touches on the reproducibility of quantum experiments and the implication of directionality in quantum states.
📊 Measuring Spin Components and Quantum Vectors
The discussion continues with the measurement of spin components and introduces the sigma z and sigma x operators, which correspond to the spin along the vertical and horizontal axes, respectively. It is noted that the apparatus always yields +1 or -1, suggesting a peculiar nature of quantum vectors. The paragraph also explores the concept of averaging in quantum mechanics and how it relates to classical vectors.
🔄 Multiple Experiments and Quantum State Reproducibility
This paragraph explores the concept of performing multiple experiments on a single quantum system or multiple identical systems. It emphasizes that the outcome of measuring a quantum system will be either +1 or -1, and that the reproducibility of results is a fundamental aspect of quantum mechanics, despite the probabilistic nature of individual measurements.
🎯 Quantum Measurement and Directional Cosines
The focus shifts to the measurement of quantum states along different axes and the use of directional cosines. The average value of a spin measured along an axis 'm', given it was originally oriented along axis 'n', is described as the cosine of the angle between the two axes. This introduces the concept of expectation values in quantum mechanics.
🧠 Quantum Logic and the Brain's Classical Constraints
This section discusses the challenges of reconciling quantum logic with our classical understanding of the world. It highlights that while our brains are classical systems, we can still attempt to understand quantum logic through experiments and the space of states of a quantum system.
⚖️ Propositions and Quantum State Verification
The paragraph explores the calculus of propositions in quantum mechanics, examining how propositions about quantum states can be combined using 'and' and 'or' operations. It questions the verification of these propositions and how they relate to the concept of quantum states.
🔵 Quantum States as Vectors in a Vector Space
This section introduces the concept that the space of states of a quantum system is a complex vector space. It explains that vectors in this space can be added and multiplied by complex numbers, and that every vector has a dual vector. The inner product of a vector with itself is discussed, as well as the concept of orthogonality between vectors.
🔴 Quantum States and Their Probabilities
The paragraph delves into the probabilities associated with quantum states, explaining that the probabilities for a state to be measured as 'up' or 'down' are given by the square of the coefficients of the state's representation in the 'up' and 'down' basis. It also states that the sum of these probabilities must equal one, indicating a complete certainty in the outcome.
🔵⚪️ Orthogonality and Physical Distinctness
The discussion continues with the concept of orthogonality in quantum mechanics, stating that when two states are physically distinguishable, they are orthogonal. It also introduces the idea that the inner product of a vector with itself equals one, which corresponds to the probabilities of all possible outcomes adding up to certainty.
🌐 Exploring the Ambiguity in Quantum State Representation
This paragraph explores the ambiguity in representing quantum states, noting that the overall phase of a state does not affect its physical properties. It discusses the freedom in choosing coefficients for a state's representation and how this freedom is constrained by the need for probabilities to sum to one.
🔍 Quantum States and Three-Dimensional Space
The final paragraph connects the discussion to the three-dimensional nature of space, explaining that the three pairs of quantum states (up/down, left/right, in/out) are symmetrically related and correspond to the three dimensions of space. It also addresses the question of whether higher-dimensional spaces would require more complex representations of quantum states.
Mindmap
Keywords
💡Qubit
💡Spin
💡Vector Space
💡Quantum Mechanics
💡Superposition
💡Measurement
💡Entanglement
💡Probability
💡Pauli Matrices
💡Observable
💡Complex Numbers
Highlights
The lecture introduces a simple quantum system consisting of one qubit, referred to as a 'spin', emphasizing its directional properties in space.
The terminology shifts from 'cubit' to 'spin' and 'pointer' to 'three vector' for clarity and to avoid confusion with classical physics concepts.
Quantum mechanics is differentiated from classical physics, noting that measurements in quantum physics inevitably alter the system being measured.
The concept of 'apparatus' is introduced as essential to the experiment, contrasting with classical physics where it is not a central consideration.
The speaker discusses the nature of quantum states and their connection with experimental apparatus, highlighting the need to consider the broader system.
An experiment is proposed where the outcome (plus or minus one) is independent of the direction of the apparatus, suggesting an intrinsic directionality to the spin.
The idea that quantum mechanics allows for reproducible experiments is highlighted, a necessity for consistent scientific understanding.
The lecture explores the concept of 'superposition' where a quantum state can exist in multiple states simultaneously, confirmed through repeated measurements.
The average value of a quantum state, when measured along different axes, is shown to behave classically, aligning with the dot product of vectors.
The speaker emphasizes the probabilistic nature of quantum mechanics, where individual measurements yield random outcomes but follow deterministic patterns over time.
The logical framework of quantum mechanics is discussed, noting that it differs from classical logic, and attempts to provide a glimpse into quantum logic.
The space of states of a quantum system is described as a set of possible states, where each state corresponds to a vector in a complex vector space.
The concept of 'orthogonality' in quantum states is introduced, explaining how it relates to the distinguishability of states through experiments.
The lecture outlines the postulate that physical states correspond to unit vectors in the vector space, with the length representing the total probability of one.
The relationship between the probabilities of different outcomes and the coefficients in the state vector is discussed, introducing the concept of probability amplitude.
The lecture concludes with a discussion on the freedom in the choice of coefficients for a quantum state vector, and the physical irrelevance of the overall phase.
An analogy is made between the complex coefficients in quantum states and the angles needed to specify the direction of a vector in three-dimensional space.
The limitations of visualization in quantum mechanics are addressed, emphasizing the probabilistic nature over deterministic classical intuitions.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: