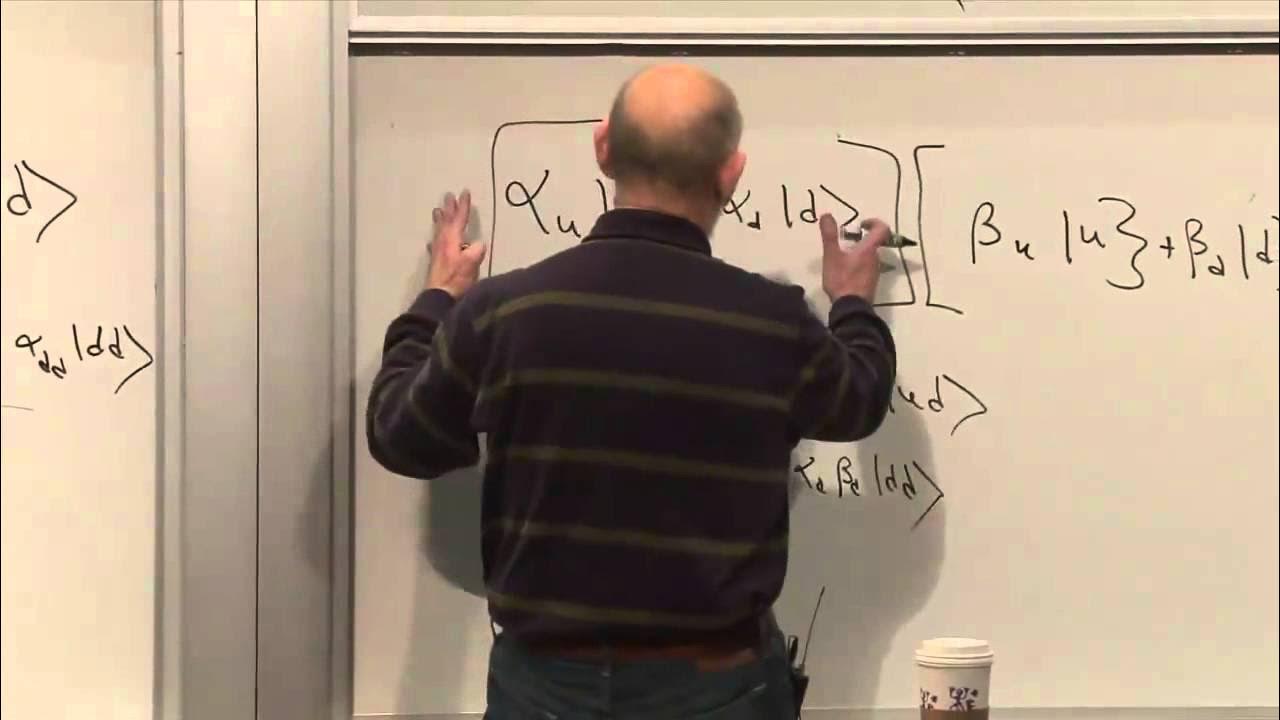Lecture 6 | Quantum Entanglements, Part 1 (Stanford)
TLDRThe transcript appears to be a lecture discussing quantum mechanics, specifically focusing on the concepts of quantum entanglement, superposition, and the implications of measurement on quantum systems. The lecturer delves into the intricacies of quantum field theory (QFT), explaining how entanglement persists even when particles are separated or when one is sent into a black hole. The discussion also covers the mathematical framework of quantum mechanics, including the role of projection operators, the concept of vector spaces and subspaces, and the probability amplitudes associated with quantum states. The lecturer further explores the collapse of the wave function, the role of interference in the famous double-slit experiment, and how measurement affects the interference pattern, leading to the destruction of superposition. The lecture concludes with a thought-provoking examination of the philosophical and practical challenges posed by quantum mechanics, particularly the non-intuitive nature of entanglement and the limitations of classical logic in explaining quantum phenomena.
Takeaways
- 🌌 The concept of entanglement in quantum physics implies that particles can remain connected even when separated by large distances, affecting each other's states instantaneously.
- ⚛️ Quantum Field Theory (QFT) discusses the possibility of virtual exchanges contributing to the entanglement of particles, despite the lack of direct interaction.
- 🧲 The state vector of a two-particle system changes when an external magnetic field is applied, yet the degree of entanglement can remain constant, reflecting the non-locality of quantum systems.
- ⚫️ When an entangled particle is introduced into a black hole, it becomes entangled with the black hole's degrees of freedom, and upon evaporation, the entanglement is transferred to the emitted photons.
- 🛁 An analogy is made with a bathtub filled with water and entangled electrons, illustrating that entanglement can extend to larger systems, such as the entire state of the bathtub, even when individual particles lose their distinct identity within it.
- 📐 The mathematical discussion of vector spaces, dimensions, and basis vectors provides a foundation for understanding the properties of quantum states and their entanglements.
- 🚫 Projection operators are used to define subspaces corresponding to specific observable properties of a system, and they play a crucial role in calculating probabilities in quantum mechanics.
- 🤝 The probability postulate in quantum mechanics is elegantly expressed through projection operators, which allow for the calculation of the likelihood that a system has a certain property.
- 🔄 The linearity of quantum mechanics ensures that the evolution of a system is consistent with the superposition principle, leading to interference patterns that are not explained by classical physics.
- 📉 The act of measurement in quantum mechanics is likened to the collapse of the wave function, which can destroy interference patterns and establish entanglement between the measured system and the measuring apparatus.
- ⏪ The Bell inequality experiment and its violation demonstrate that quantum mechanics cannot be explained by a statistical theory of classical systems, highlighting the fundamentally different nature of quantum correlations.
Q & A
What is the significance of the Stanford University program in the context of this transcript?
-The program appears to be an educational lecture or seminar on quantum mechanics, specifically discussing concepts like quantum field theory (QFT), entanglement, and the mathematical framework of quantum mechanics. Stanford University is likely the institution hosting or organizing this program.
What does the term 'singlet state' refer to in the context of quantum mechanics?
-In quantum mechanics, a 'singlet state' is a state of a quantum system in which two or more particles are in a superposition such that the overall wave function is antisymmetric. This often refers to the total spin of a particle pair being zero, indicating that the particles are in opposite spin states.
How does the concept of 'entanglement' apply to the particles discussed in the transcript?
-Entanglement is a quantum mechanical phenomenon where the quantum states of two or more objects have to be described with reference to each other, even though the individual objects may be spatially separated. In the transcript, entanglement is discussed in the context of a pair of particles where the state of one (such as its spin) is immediately correlated with the state of the other, regardless of the distance between them.
What is the role of a 'projection operator' in quantum mechanics?
-A projection operator in quantum mechanics is a linear operator that acts on a Hilbert space, projecting a given vector onto a subspace. It is used to calculate the probability of finding a system in a particular state and is central to the concept of quantum measurement, where it can determine whether a system has a certain property.
What is the 'Bell inequality', and why is it significant in the context of quantum mechanics?
-The Bell inequality is a mathematical inequality involving correlation coefficients, which, if violated, indicates that the quantum system cannot be described by a local hidden variable theory—a classical understanding of reality. It is significant because it provides a way to test the nonlocal nature of quantum mechanics against classical theories.
How does the concept of 'superposition' relate to the movement of particles in the two-slit experiment?
-Superposition is a fundamental principle of quantum mechanics where a particle can exist in multiple states simultaneously. In the two-slit experiment, an electron is said to be in a superposition of states as it travels towards the two slits. This superposition allows the electron to interfere with itself, leading to the interference pattern observed on the detection screen.
What is the 'collapse of the wavefunction', and how does it relate to the act of measurement in quantum mechanics?
-The collapse of the wavefunction is a process in quantum mechanics where the quantum system transitions from a superposition of states to a single state due to a measurement. This concept is central to understanding how quantum systems behave when observed or measured, leading to the loss of interference patterns and the apparent 'choice' of a definite state.
What does the term 'dimension' refer to in the context of a vector space?
-In the context of a vector space, 'dimension' refers to the maximum number of linearly independent vectors that can be found within that space. It is a measure of the space's capacity to accommodate linearly independent directions or states.
How does the concept of 'linear independence' apply to vectors in a vector space?
-Linear independence in a vector space means that no vector in a set of vectors can be expressed as a linear combination of the other vectors in the set. It is a fundamental concept that underpins the structure of the vector space, ensuring that vectors do not share the same direction.
What is the significance of 'eigenvalues' and 'eigenvectors' in the context of quantum mechanics?
-In quantum mechanics, eigenvalues and eigenvectors are associated with the possible results of measurements and the states of quantum systems, respectively. An eigenvalue corresponds to a measurable property of a system, and an eigenvector represents the state of the system for which the measurement is certain.
How does the 'two-slit experiment' demonstrate the principles of quantum mechanics?
-The two-slit experiment demonstrates the principles of quantum mechanics by showing how particles like electrons can display wave-like interference patterns when both slits are open, indicating their superposition. However, if measurements are made to determine through which slit the particle passes, the interference pattern is lost, illustrating the collapse of the wavefunction and the principle of observation affecting the outcome.
Outlines
😀 Quantum Entanglement and Virtual Exchange
The first paragraph delves into the concept of quantum field theory (QFT) and quantum entanglement. It discusses the idea of a singlet state with spaceflight separation and the notion of virtual exchange. The speaker contemplates what happens when particles are entangled and how their states are affected by external influences, such as a magnetic field. The concept of entanglement measures is introduced, emphasizing that entanglement persists despite changes in the system. The paragraph also explores the implications of entangling particles with black holes and the idea of disentanglement through interaction.
📚 Projection Operators and Subspaces
The second paragraph focuses on the mathematical foundations of quantum mechanics, specifically projection operators and subspaces. It explains the concept of vector spaces, dimensions, and the relationship between linear dependence and independence. The paragraph also discusses the role of dual vectors, orthogonality, and the importance of basis vectors in defining a space. It touches on the theorem that any vector can be expanded in terms of its basis vectors and how this relates to the coefficients in the expansion.
🧲 Properties of Vector Spaces and Observables
The third paragraph explores the properties of vector spaces, particularly the existence of orthogonal basis vectors. It explains that in a d-dimensional vector space, one can always find d orthogonal basis vectors that are normalized. The paragraph also introduces the concept of a particle moving in space and the degrees of freedom associated with it. Furthermore, it discusses the idea of a resolution of identity and how it relates to the unit operator and basis vectors.
🚪 Subspaces and Eigenvalues
The fourth paragraph discusses subspaces corresponding to certain observable questions and the concept of eigenvalues. It explains that if two eigenvectors share the same eigenvalue, any linear combination of these vectors will also be an eigenvector with the same eigenvalue. The paragraph also introduces the idea of a subspace spanned by vectors with the same eigenvalue and how this subspace can be identified with a particular property of an observable.
🌐 Basis Within a Subspace
The fifth paragraph focuses on finding a basis within a subspace. It explains that once a subspace is identified, one can find basis vectors that span only that subspace. The paragraph also discusses the properties of these basis vectors, such as orthogonality and the ability to construct a projection operator onto the subspace. It highlights the importance of these concepts in quantum mechanics and how they relate to the measurement process.
🎚 Probability Postulate in Quantum Mechanics
The sixth paragraph explains the probability postulate in quantum mechanics and its relation to projection operators. It states that the probability of a system having a particular property is given by the expectation value of the corresponding projection operator. The paragraph also discusses the concept of commuting projection operators and the implications for the simultaneous measurement of two properties. It touches on the idea of 'and' and 'or' statements in the context of quantum mechanics.
🤔 Bell's Theorem and Quantum States
The seventh paragraph discusses Bell's theorem and its implications for quantum states. It explains that if a quantum state satisfies Bell's inequality, it cannot be described by a classical statistical theory. The paragraph also explores the idea of measuring different properties of a quantum system and how this can lead to the violation of Bell's inequality. It concludes by emphasizing the non-classical nature of quantum mechanics and the importance of understanding its unique properties.
🔬 Two-Slit Experiment and Quantum Evolution
The eighth paragraph describes a simplified version of the two-slit experiment, focusing on the linear evolution of quantum states. It explains that if an electron starts at a certain position, it evolves into a superposition of states due to the linearity of quantum mechanics. The paragraph also discusses the implications of this linearity for the probability of finding the electron in different positions after it passes through the slits.
🧬 Entanglement and Measurement in Quantum Systems
The ninth paragraph explores the concept of entanglement and its role in the measurement process in quantum systems. It discusses how the act of measurement can lead to the entanglement of a quantum system with a measuring device, and how this entanglement can destroy the interference pattern observed in the two-slit experiment. The paragraph also touches on the idea of weak and strong measurements, and how they affect the quantum state.
🌌 Collapse of the Wavefunction and Disturbance
The tenth paragraph delves into the collapse of the wavefunction and how it relates to the disturbance caused by measurements. It explains that if a quantum system interacts with the environment in a way that allows for the determination of a particular property, the interference pattern is destroyed. The paragraph also discusses the role of energy gaps in systems and how they can affect the ability of a quantum system to create a disturbance, leading to the preservation or destruction of the interference pattern.
🔍 Repeated Experiments and Statistical Significance
The eleventh paragraph emphasizes the importance of repeated experiments in quantum mechanics to observe statistical patterns, such as interference patterns. It clarifies that while a single electron cannot display an interference pattern, the accumulation of data from many identical experiments can reveal the probabilistic nature of quantum phenomena. The paragraph also touches on the concept of weak measurements and how they can provide partial information about the quantum state without fully collapsing the wavefunction.
Mindmap
Keywords
💡Quantum Entanglement
💡Projection Operators
💡Vector Space and Dimension
💡Superposition
💡Bell's Theorem
💡Wavefunction Collapse
💡Observables
💡Linearity of Quantum Mechanics
💡Subspace
💡Eigenvalues and Eigenvectors
💡Two-Slit Experiment
Highlights
Exploration of quantum entanglement and its implications within the framework of Quantum Field Theory (QFT).
Discussion on the concept of virtual exchange in QFT and its role in particle entanglement.
Insight into the behavior of entangled particles and how their state vectors change under different conditions, such as the application of a magnetic field.
Explanation of how entanglement measures remain constant even when the system's form changes.
The impact of entanglement on particles when one is introduced to a black hole, and how it relates to the black hole's evaporation process.
Illustration of how entanglement can expand to include larger systems, such as a bathtub filled with water and its effect on particle states.
Discussion on the possibility of disentangling particles and the conditions required for entanglement to occur.
Introduction to the mathematical concepts of vector spaces, dimensions, and the role of orthogonality in quantum states.
Explanation of the dimension of a vector space and its relation to the maximum number of linearly independent vectors.
The theorem of finding a basis for a vector space and its importance in quantum mechanics.
Introduction to projection operators and their significance in defining subspaces and observable properties in quantum systems.
Discussion on the probability postulate in quantum mechanics and how it relates to the expectation value of projection operators.
Explanation of the concept of interference, its connection to measurement phenomena, and the role of entanglement in the collapse of the wave function.
The two-slit experiment simplified to illustrate the principles of quantum superposition and interference.
How the act of measurement can lead to the destruction of interference patterns and the concept of wave function collapse.
The role of environmental factors in entanglement and interference, such as the effect of cooling down apparatuses to prevent decoherence.
Discussion on the concept of weak and strong measurements in quantum systems and their effects on entanglement and interference patterns.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: