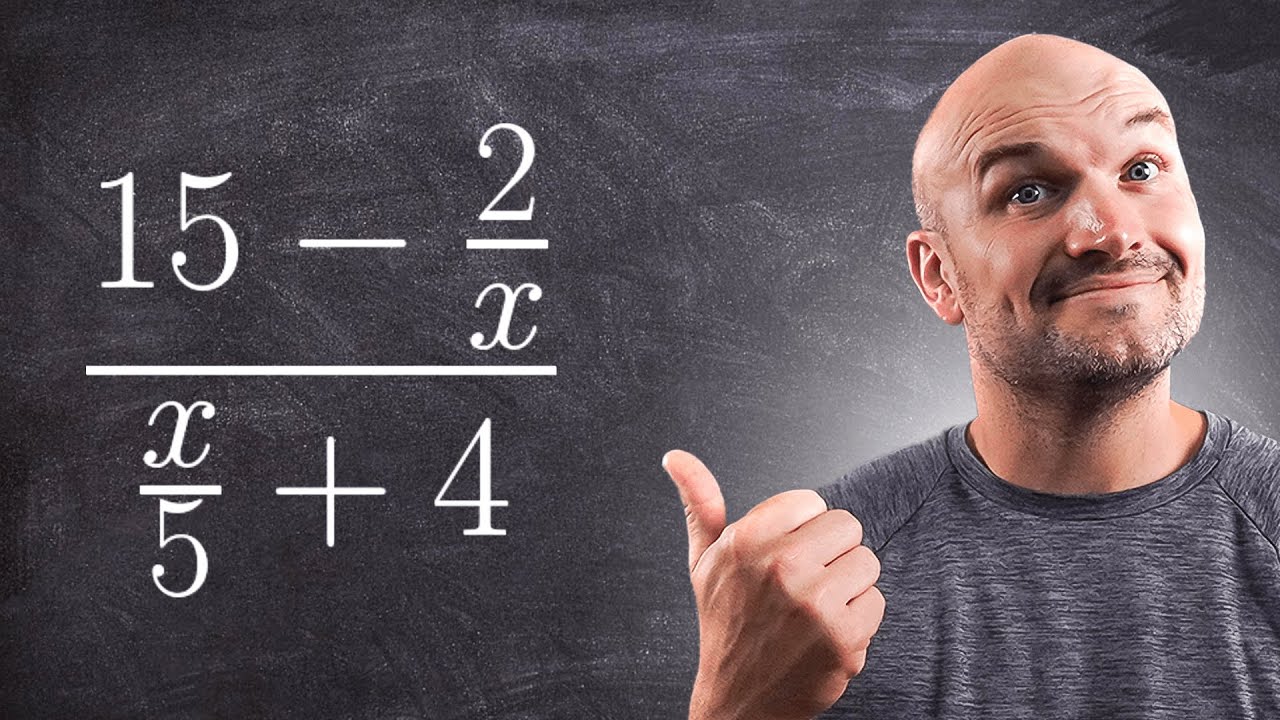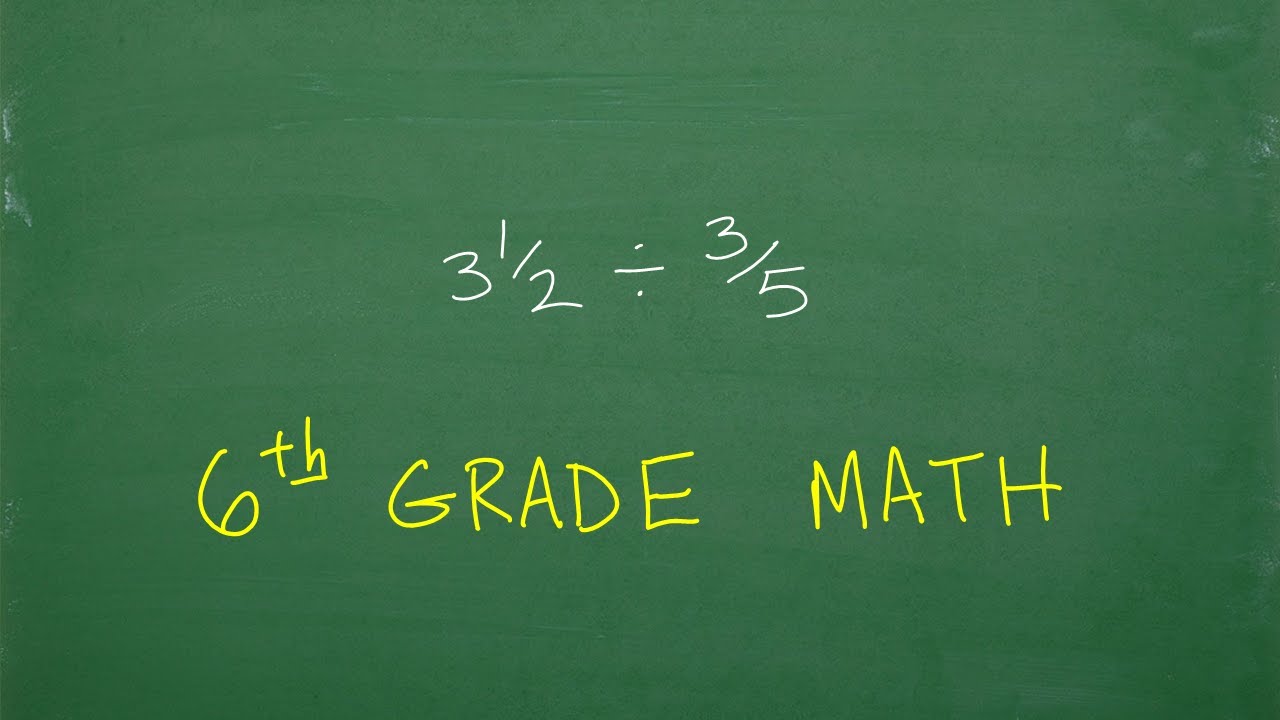Multiplication and Division of Fractions
TLDRThe video script covers multiplying and dividing fractions, building on prior knowledge of adding and subtracting fractions. It explains that when multiplying a fraction by a whole number, only the numerator is affected. When multiplying two fractions, the numerators and denominators are multiplied. Conceptually, this can be thought of as multiplying by the numerator and dividing by the denominator. Division rules are also covered - dividing a fraction by a whole number divides the numerator, and dividing fractions involves multiplication by the reciprocal. Care must be taken not to divide by zero, which is undefined. Overall, the key concepts around fraction multiplication and division are clearly explained.
Takeaways
- 😀 When multiplying a fraction by a whole number, only the numerator changes
- 😉 To multiply two fractions, multiply the numerators together and multiply the denominators together
- 🤔 When multiplying fractions, you can think of it as multiplying by the numerator and dividing by the denominator
- 😯 Dividing a fraction by a whole number only divides the numerator
- 😀 Dividing a fraction is the same as multiplying by the reciprocal
- 👍 To divide two fractions, flip the second fraction and multiply
- 😠 You cannot divide by zero - it results in an undefined value
- 🤓 Adding fractions requires a common denominator, but multiplying fractions does not
- 😀 Multiplying fractions is straightforward - just multiply straight across
- 🧐 Understanding fractions as division is helpful for operations like multiplication and division
Q & A
What happens when you multiply a fraction by a whole number?
-When you multiply a fraction by a whole number, the whole number multiplies only the numerator of the fraction. The denominator stays the same.
Why doesn't the denominator change when you multiply a fraction by a whole number?
-The denominator represents the magnitude or size of the fractional piece. Multiplying by a whole number increases the number of fractional pieces but does not change their size.
What do you do when multiplying two fractions together?
-When multiplying two fractions, multiply the numerators together to get the new numerator and multiply the denominators together to get the new denominator.
How can you think about multiplying two fractions conceptually?
-You can think of multiplying two fractions as multiplying by the numerator and then dividing by the denominator. This helps explain why the denominator increases in size.
Why can you multiply any two fractions even if they have different denominators?
-The relative size of pieces represented by the denominators is maintained when you multiply the denominators. This allows fractions with different sized pieces to be combined.
What happens when you divide a fraction by a whole number?
-Dividing a fraction by a whole number is the same as multiplying by the whole number's reciprocal. So only the numerator changes, the denominator stays the same.
Why is dividing by a whole number similar to multiplying by a fraction?
-Dividing by a number is conceptually the same as multiplying by its reciprocal. So dividing by 2 is like multiplying by 1/2 which changes the numerator when working with fractions.
How do you divide one fraction by another fraction?
-To divide by a fraction, you flip the second fraction and multiply. So a/b ÷ c/d = a/b × d/c. The denominators multiply and the numerators multiply.
Why can you not divide by zero when working with fractions?
-Dividing by zero is undefined mathematically. It does not represent dividing a quantity into no pieces, which division by 1 would imply. The result is simply undefined.
What have we learned about multiplying and dividing fractions?
-We learned how to multiply fractions by whole numbers and other fractions, which multiplies numerators and denominators. We also learned to divide fractions by flipping the divisor and multiplying.
Outlines
😃 Multiplying and Dividing Fractions
This paragraph explains how to multiply and divide fractions. It covers multiplying a fraction by a whole number, which only affects the numerator, as well as multiplying any two fractions, which involves multiplying the numerators and denominators. It also explains dividing a fraction by a whole number, which only divides the numerator, and dividing fractions by other fractions using the 'flip and multiply' method. The paragraph notes that dividing by 0 results in an undefined value.
Mindmap
Keywords
💡fraction
💡numerator
💡denominator
💡reciprocal
💡reduce
💡multiply
💡divide
💡undefined
💡whole number
💡magnitude
Highlights
When multiplying a fraction by a whole number, only the numerator changes.
The denominator tells us the magnitude of the fraction, not how many there are.
When multiplying fractions, multiply the numerators together and denominators together.
Multiplying fractions is like multiplying by the numerator and dividing by the denominator.
Dividing by a whole number only divides the numerator.
Dividing by a number is the same as multiplying by its reciprocal.
When dividing fractions, flip the second fraction and multiply.
We can't divide by zero because it is undefined.
Adding fractions requires a common denominator, but multiplying does not.
A whole number can be seen as a fraction with denominator 1.
Multiplying fractions is different than adding them.
An example is showing 2/3 x 1/2 = 1/3.
Another example is 5/6 x 3/4 = 15/24.
Dividing by 2 gives you half of the starting amount.
Let's check comprehension on multiplying and dividing fractions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: