Types of Angles and Angle Relationships

Professor Dave Explains
16 Oct 201707:24
EducationalLearning
32 Likes 10 Comments

TLDRThe script discusses angles formed by intersecting lines. It defines key terms like acute, obtuse, complementary, and supplementary angles. It explains vertical angles are equal and adjacent angles formed by intersecting lines are supplementary. It covers parallel lines and the relationships between angles created when a line intersects parallel lines. These include alternate interior, alternate exterior, corresponding, and same-side interior angles. It sets up equations to algebraically solve for unknown angles based on these relationships. Finally, it transitions to discussing triangles, the simplest polygon with 3 straight line segment sides, setting the stage for future geometry lessons.

Takeaways
  • 😀 Angles are independent measurements of how open or closed lines are in relation to each other.
  • 😯 There are 360 degrees in a full circle. Angles are measured in degrees based on their proportion of a full circle.
  • 😮 Angles less than 90 degrees are called acute angles. 90 degree angles are right angles. Angles between 90-180 degrees are obtuse angles.
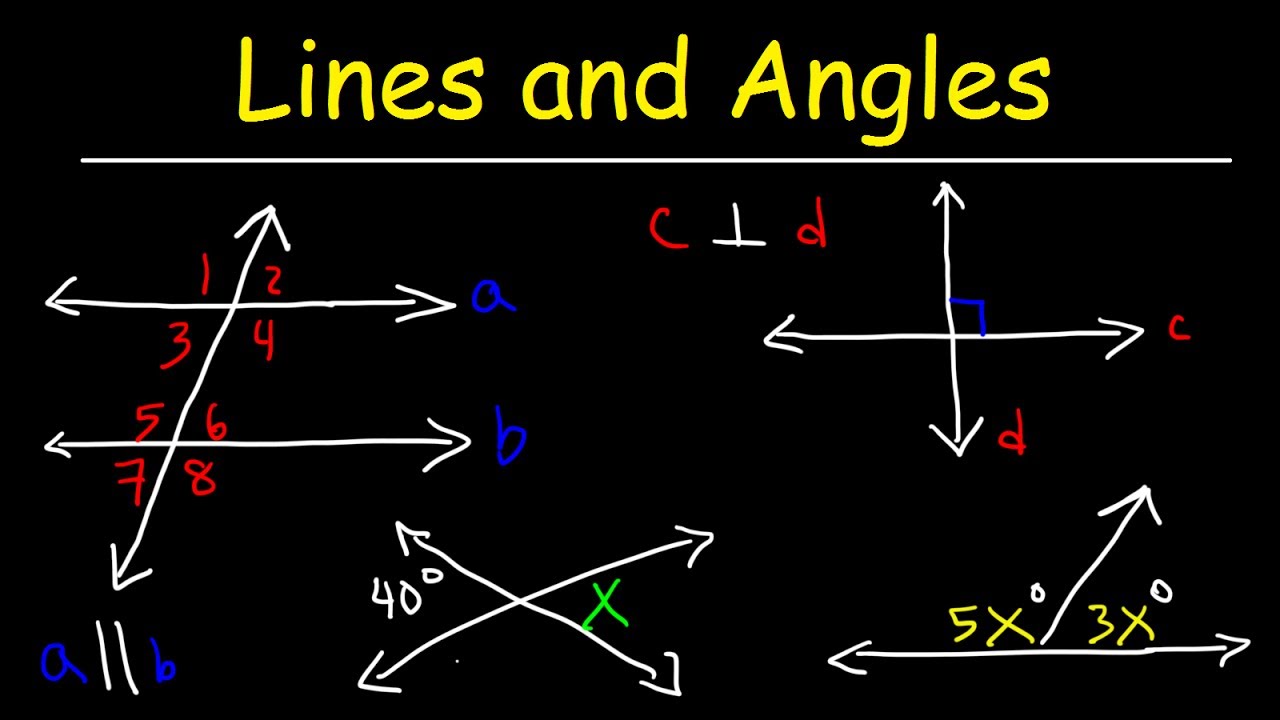
  • 📐 Vertical angles (across from each other when two lines cross) are always equal. Adjacent angles formed when two lines cross are supplementary.
  • 🤓 Alternate interior angles formed when a line crosses two parallel lines are equal. Same for alternate exterior angles.
  • 🧐 Interior angles on the same side of the transversal across parallel lines are supplementary (add to 180 degrees).
  • 👌 Corresponding angles in parallel lines crossed by a transversal occupy the same relative position and are equal.
  • 📏 Perpendicular lines intersect at a 90 degree right angle. Parallel lines never intersect.
  • 🔺 The minimum shape formed by straight line segments is a triangle, which has 3 line segments.
  • ✏️ Algebra can be used to solve for unknown angles based on rules about relationships between angles.
Q & A

  • What is an angle and how does it relate to the opening of a door?

    -An angle is a measurement that represents how open something is, like a door, independently of the actual dimensions involved. It simply refers to the space between two lines or rays anchored at a common point.

  • What are the three main types of angles?

    -The three main types of angles are: acute angle (<90 degrees), right angle (=90 degrees), and obtuse angle (>90 degrees but <180 degrees).

  • What is the relationship between vertical angles?

    -Vertical angles are angles that are directly across from each other when two lines cross. They are always equal in their degree measurement.

  • What are supplementary, complementary, alternate interior, alternate exterior, corresponding and same-side interior angles?

    -These are all terms used to describe specific angle relationships when parallel lines are crossed by a transversal line. Supplementary angles add to 180 degrees. Complementary angles add to 90 degrees. Alternate angles are equal. Same-side interior angles are supplementary.

  • How can you use known angle relationships to solve for unknown angles in a diagram?

    -Using rules like angles vertical to each other being equal, alternate angles being equal, etc., you can set up equations and algebraically solve for unknown angle measurements.

  • What is significant about intersecting lines forming 90 degree angles?

    -When two intersecting lines form 90 degree angles, they are called perpendicular lines.

  • What are parallel lines?

    -Parallel lines are two lines in the same plane that never intersect each other, no matter how far they are extended.

  • What are some key terms used when describing angles formed by parallel lines intersected by a transversal?

    -Some key terms are: interior angles, exterior angles, alternate interior angles, alternate exterior angles, corresponding angles.

  • What is required to form a polygon shape?

    -At minimum, three line segments connected end to end are required to form a simple polygon shape like a triangle.

  • What is discussed after introducing angles and shapes formed from lines?

    -After discussing angles and shapes like triangles formed from lines, the script says the next topic will be learning about different types of triangles.

Outlines
00:00
😀 Introducing Angles

This paragraph introduces the concept of angles. It explains that angles are a way to measure how two lines intersect or how open a door is, independent of any spatial dimensions. It shows how to construct an angle with two rays sharing a common endpoint called the vertex. It discusses measuring angles in degrees going from 0 to 180 to 360 degrees in a full circle. It also defines acute, right, and obtuse angles.

05:00
😀 Angle Relationships and Special Lines

This paragraph discusses several special types of angles and lines. It covers vertical angles which are equal, adjacent angles, complementary angles that add to 90 degrees, perpendicular and parallel lines, interior vs exterior angles when two parallel lines are crossed by a third line. It also mentions several angle theorems like alternate interior, alternate exterior, and same-side interior angles.

Mindmap
Keywords
💡angle
An angle is a measure of the space between two intersecting lines or rays. It represents how open or closed the lines are relative to each other, independent of their dimensions. Angles are essential in geometry for analyzing shapes and spatial relationships. The video introduces different types of angles like acute, right, and obtuse angles.
💡vertex
The vertex refers to the shared endpoint where two rays or lines meet to form an angle. Changing the position of the rays while anchoring the vertex point changes the measure of the angle between them.
💡degrees
Degrees are one common unit used to measure angles. There are 360 total degrees in a complete circle. Measuring angles in degrees allows geometric relationships to be quantified precisely.
💡vertical angles
Vertical angles are angles opposite from each other when two lines intersect. An important geometric property is that vertical angles formed by intersecting lines are always equal in measure.
💡supplementary angles
Supplementary angles are two angles whose measures add up to 180 degrees. They are formed when two lines intersect. Understanding supplementary angles allows unknown angles to be determined algebraically in geometry problems.
💡parallel lines
Parallel lines are two lines that lie in the same plane but never intersect each other, no matter how far extended. Analyzing the relationships between parallel lines and transversal lines allows more geometric properties and theorems to be discovered.
💡triangle
A triangle is a three-sided polygon shape that requires at least three straight line segments connected at their endpoints. Triangles are one of the simplest geometric shapes but can be analyzed from many angles using concepts like angles and parallel lines.
💡acute angle
An acute angle measures less than 90 degrees. The video uses the mnemonic that acute angles are cute and tiny to help remember the definition. Recognizing acute versus obtuse angles is essential for geometric analysis.
💡right angle
A right angle measures exactly 90 degrees. It is denoted with a square symbol and is important in geometry. When two lines intersect at a right angle, they are called perpendicular lines.
💡obtuse angle
An obtuse angle measures between 90 and 180 degrees. It is wider than a right angle. Being able to classify angles as acute, right, or obtuse supports understanding their relationships in geometric diagrams.
Highlights

Angles are independent of dimensions and ubiquitous in everyday life.

Vertex is the common point where two rays start to form an angle.

Degrees are a common way to measure angles. 360 degrees in a circle.

Acute angle is less than 90 degrees. Right angle is 90 degrees. Obtuse angle is between 90 and 180 degrees.

Vertical angles formed by intersecting lines are always equal.

Adjacent angles formed by intersecting lines are supplementary.

Complementary angles add up to 90 degrees.

Perpendicular lines intersect at 90 degree angles.

Parallel lines never intersect.

Angles formed between parallel lines have special relationships.

A triangle is the simplest polygon with 3 line segments.

Using angles, parallel lines, and shapes in algebra problems.

Alternate interior angles formed by parallel lines crossing a transversal are equal.

Same-side interior angles formed by parallel lines are supplementary.

Corresponding angles formed by parallel lines are equal.

Transcripts

Browse More Related Video

Parallel & Perpendicular Lines, Alternate Interior & Exterior Angles, Transversals

Parallel and Perpendicular Lines, Transversals, Alternate Interior Angles, Alternate Exterior Angles

College Physics 1: Lecture 2 - Mathematics Review (Part 2)

Basic Euclidean Geometry: Points, Lines, and Planes

Introduction to Angles

MATH & GEOMETRY Vocabulary and Terminology in English

Rate This

5.0 / 5 (0 votes)

Thanks for rating: