Introduction to Algebra: Using Variables
TLDRThis video introduces algebra, explaining that it builds on arithmetic by using variables instead of just numbers. Variables represent quantities that can change, like gas prices or plane speeds. Algebraic expressions include variables, numbers, and operations. The video shows how to evaluate expressions by plugging in values for the variables. It explains how algebra models real-world situations through equations relating variables. Using examples about buying cheeseburgers and hours of TV watching, it demonstrates how to set up algebraic relationships. More details on algebraic properties are provided to lay the groundwork for solving algebraic problems.
Takeaways
- 😀 Algebra uses symbols like arithmetic does and is quite easy to make intuitive
- 👍 Variables in algebra represent quantities that can change, unlike constants
- 📈 Algebraic expressions include variables, numbers and operations, like 3x + 2
- 🖊 We can evaluate algebraic expressions by plugging in values for the variables
- 📊 Algebra allows us to model real-world situations with equations
- 🔢 If X represents one quantity, we can relate other quantities to it algebraically
- 🧮 Setting up the equation is the key to using algebra effectively
- 📺 We set up an equation relating hours of TV watched: Y = 2X + 1
- ⛓ Algebraic relationships let us do powerful things by relating quantities
- 🤓 There's more to learn about algebraic properties before diving in deeper
Q & A
What is the difference between a variable and a constant in algebra?
-A variable is a letter or symbol that represents a quantity that can change. A constant is a letter or symbol that represents a quantity that does not change.
What does the algebraic expression 3x + 2 allow us to do?
-The algebraic expression 3x + 2 allows us to evaluate the expression for any value of x we choose by plugging in the value for x. This is useful for modeling real-world situations.
How can algebra be used to model the cost of cheeseburgers?
-We can set up an equation relating Y, the total cost, to X, the number of cheeseburgers, using the fact that each cheeseburger costs $3. So Y = 3X represents the total cost based on the number of cheeseburgers purchased.
What does the equation Y = 2X + 1 represent in the TV watching example?
-In the example, X represents the number of hours you watch TV, and Y represents the number of hours your friend Bobo watches TV. The equation shows that Bobo watches twice as many hours as you do, plus an additional hour on top of that.
What makes algebra more powerful than just using arithmetic?
-Algebra allows us to set up equations that model real-world situations with unknown quantities represented by variables. We can then use these algebraic relationships to calculate a wide variety of values based on changing inputs, which is more flexible and powerful than strict arithmetic.
What operations can be used in algebraic expressions besides multiplication?
-Algebraic expressions can include addition, subtraction, division, and exponentiation operations as well as multiplication. Grouping symbols like parentheses can also be used to control order of operations.
What does it mean to evaluate an algebraic expression?
-To evaluate an algebraic expression means to substitute a numeric value for any variable(s) in the expression and calculate the result. For example, evaluating 3x+2 when x=5 means replacing x with 5 everywhere, resulting in 3*5+2 = 15+2 = 17.
How are equations and expressions different in algebra?
-Expressions represent a mathematical calculation with variables, but do not have an equals sign setting one side equal to the other. Equations make use of the equals sign to state that two sides have the same value.
What are some examples of things algebra can be used to model?
-Algebra can be used to model: costs related to a quantity purchased, distances traveled based on rate and time, compound interest calculations, optimization problems, population growth rates, projectile motion physics problems, and many other real-world situations involving unknown or changing quantities.
What makes algebra seem less daunting compared to plain old math?
-Using symbols and letters for unknown values makes algebra seem less scary. Also realizing algebraic expressions work similarly to arithmetic with numbers substituted for variables shows algebra builds straightforwardly on previous math knowledge.
Outlines
📚 Introducing Algebra
This paragraph introduces algebra, explaining that it uses symbols like arithmetic but allows you to model real-world situations and make calculations more flexibly. It distinguishes variables, which can change, from constants. An example algebraic expression 3x + 2 is evaluated for different x values.
📺 Setting Up Equations to Model Situations
This paragraph explains how algebraic equations can model real-world situations, using examples of calculating the cost of cheeseburgers and relating the hours of TV you and your friend Bobo watch. The equations allow a variety of pertinent calculations.
❗ There's More to Learn Before Solving Algebra
This closing paragraph indicates there are more algebraic properties to learn before starting to do lots of algebra problems, so it transitions to moving forward with that.
Mindmap
Keywords
💡algebra
💡variable
💡expression
💡equation
💡evaluate
💡constant
💡model
💡relationship
💡simplify
💡properties
Highlights
Algebra uses symbols just like arithmetic does, and it is quite easy to make these symbols intuitive
In math, a variable is a letter or symbol that represents a quantity that can change
Whereas with arithmetic our equations simply contain numbers and arithmetic operations, an algebraic expression will always include one or more variables
We can evaluate this expression for any value of x that we choose, we simply plug the value into the expression
This is useful, because we can use algebraic equations to model real-world situations and make meaningful statements about them
The trick is just knowing how to set up the equation
These kinds of algebraic relationships allow us to do some pretty powerful things
Before we start doing lots of algebra, there’s a bit more to learn about algebraic properties
Algebraic expressions will always include one or more variables, as well as some numbers and operations
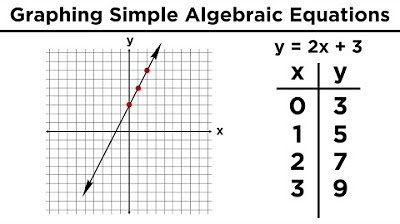
We can make a table as we evaluate algebraic expressions for different values
Algebra allows us to set up relationships that do a variety of relevant calculations
We can relate unknown quantities with algebraic equations
Algebra translations real-world situations into symbolic mathematical relationships
Algebra moves beyond basic arithmetic into more powerful mathematical territory
Algebra may seem scary at first but becomes intuitive with practice
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: