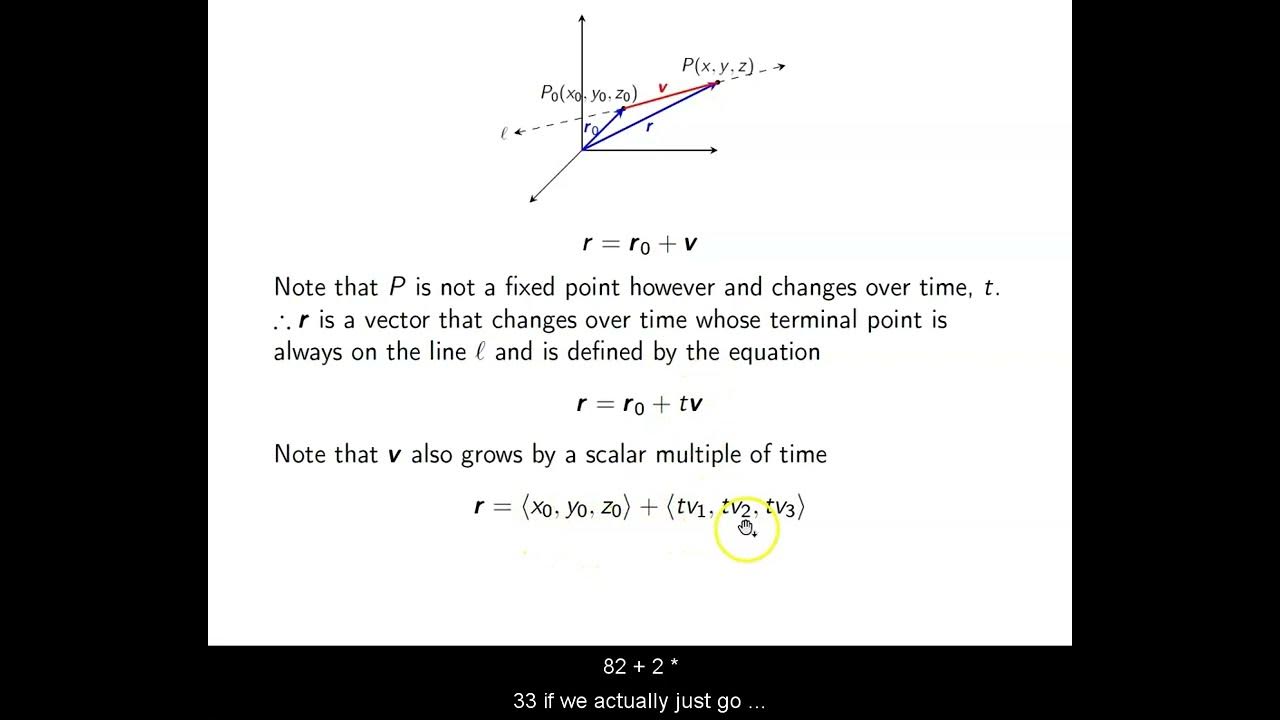
Basic Euclidean Geometry: Points, Lines, and Planes
TLDRThe script discusses fundamental Euclidean geometry concepts starting with zero-dimensional points, then builds up to one-dimensional lines by connecting points, two-dimensional planes by connecting lines perpendicular to each other, and three-dimensional space by stacking planes. It explains that any two points determine a line, and any three non-collinear points determine a plane. These are idealized conceptual building blocks, as even a sheet of paper has some thickness. The script then defines related terminology like rays and line segments before transitioning to a discussion of angles formed by intersecting lines.
Takeaways
- 😀 Euclidian geometry built on earlier work and describes mathematical axioms and postulates
- 😲 A point is a 0D location in space represented by a dot
- 😎 A line is made of infinite points along one dimension
- 📏 A plane contains infinite parallel lines along another dimension
- 🌐 3D space contains infinite parallel planes
- 👥 Any 2 points define a line, any 3 non-collinear points define a plane
- 🤓 These are idealized concepts, planes can't be infinitely thin
- 🧠 But they let us approximate and draw conclusions
- 🔺 A ray has 1 endpoint, a line segment has 2 endpoints
- 📐 Lines, rays and segments form figures and angles to analyze
Q & A
What are the key geometric constructs that Euclidean geometry describes?
-Euclidean geometry describes points, lines, planes, and space. It defines their properties and relationships through a set of axioms and postulates.
How is a line defined in geometry?
-A line is defined as an infinite set of points strung along a single dimension.
What distinguishes a plane from a line?
-A plane is two-dimensional, defined by an infinite set of lines strung along a dimension perpendicular to the lines. A line has only one dimension.
How can two points define a line?
-Any two distinct points define a unique line that passes through both of them. There is only one line that contains both points.
When can three points define a plane?
-Three points define a plane only when they are not collinear (i.e. do not lie on the same line). If the three points are not in a straight line, there is a unique plane containing all three.
What are some differences between lines, rays and line segments?
-Lines extend infinitely in two directions, rays extend infinitely in one direction from an endpoint, and line segments are finite chunks of lines with two endpoints.
Why are planes described as infinitely thin?
-Planes are idealized as perfectly two-dimensional objects with no thickness. Real physical planes have some non-zero thickness but can be approximated as thin.
How are angles related to lines?
-Angles are formed wherever two lines intersect. The magnitude of angles depends on the degree of rotation between the lines.
Why is Euclidean geometry useful even if physical shapes are imperfect?
-Though real objects do not match platonic ideals, Euclidean abstractions allow systematic logical deductions applicable to approximate real situations.
What are some basic shapes created from lines and angles?
-Basic Euclidean shapes created from lines and angles include triangles, rectangles, and polygons with different numbers of sides.
Outlines
📝 Defining Key Geometric Concepts
This paragraph introduces basic geometric concepts such as points, lines, planes, and spaces. It explains that a point has zero dimensions, a line is formed by stringing points along one dimension, a plane by lining up lines perpendicular to each other, and space consists of stacking multiple planes. Other key ideas include linear relationships between these concepts, idealized versus physical representations, and related terminology like rays and line segments.
👁️ Examining Angles Between Lines
The final paragraph indicates that various angles can be formed between lines and their relationships and properties warrant further discussion. This foreshadows more intricate geometric ideas to be covered next.
Mindmap
Keywords
💡Euclidian geometry
💡point
💡line
💡plane
💡dimension
💡space
💡angle
💡endpoint
💡idealization
💡approximation
Highlights
Geometry was developed in ancient Greece, and when we learn this geometry, we refer to it as Euclidean geometry, in reference to Euclid.
Euclid's work describes a set of axioms and postulates from which a variety of theorems can be derived.
A point is a zero-dimensional location in space. We represent points with dots, realizing the dot is infinitely larger than the point.
A line is a one-dimensional object formed by stringing an infinite number of points along a dimension.
A plane is a two-dimensional object formed by stringing infinite lines perpendicular to each other.
Three-dimensional space is formed by stringing infinite planes.
Two points define a line, as there is only one line containing both points. Three non-collinear points define a plane.
These figures are idealized concepts. No real plane has only two dimensions.
Conclusions from idealized figures apply approximately in the physical world.
A ray has one endpoint, while a line segment has two endpoints.
Lines, rays and segments can generate figures with differing numbers of sides and angles between them.
There are relationships between the types, magnitudes and angles that are possible.
Angles and their relationships will be discussed further.
Geometry was foundational for developing abstract mathematics with wide applications.
Euclid built on previous work to compile the definitive basis still used today.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: