Lecture 5 | Quantum Entanglements, Part 1 (Stanford)
TLDRThe video script is an in-depth exploration of quantum entanglement, focusing on the properties of entangled states of two electrons. It explains the concept of linear superposition and the correlation between the spins of entangled particles. The script delves into the action of various sigma operators on electron states and discusses the expectation values of spin components. It also highlights the difference between the singlet and triplet states of entangled electrons, emphasizing the unique correlation in the singlet state where measuring one spin instantly determines the state of the other. The discussion then transitions into the implications of Bell's theorem and inequality, illustrating that quantum mechanics cannot be replicated by any underlying classical system. The script concludes with a consideration of the no-cloning theorem, which states that it is impossible to create a machine that can clone an arbitrary unknown quantum state, thereby preserving the unique properties of quantum entanglement.
Takeaways
- 📚 The concept of quantum entanglement is introduced, where two particles like electrons can be interconnected in such a way that the state of one (spin up or down) instantly influences the state of the other, regardless of distance.
- 🚫 The no-cloning theorem is discussed, which states that it is impossible to create an identical copy of an arbitrary unknown quantum state; this is a fundamental principle of quantum mechanics.
- 🔬 The script touches on the Heisenberg uncertainty principle and how entanglement seems to challenge it, but it is clarified that measuring one property of an entangled particle does not violate the principle.
- 🤔 The nature of quantum logic and set theory is explored, highlighting that in quantum mechanics, properties correspond to subspaces of a vector space rather than subsets of a set, which is a key difference from classical logic.
- 🧲 The role of projection operators in quantum mechanics is explained, which project a quantum state onto a subspace corresponding to a particular property or measurement outcome.
- 📉 Bell's theorem and inequality are mentioned, showing that certain correlations between entangled particles cannot be explained by classical physics and suggesting that quantum mechanics cannot be simulated by a classical system.
- 🌐 The importance of the linearity of quantum mechanics is emphasized, which means that a system in a superposition of states will evolve into a superposition of the evolved states.
- ⏲️ Time evolution of quantum states is briefly mentioned, noting that it is linear and that this property is well-supported by experimental evidence.
- 🔍 The script discusses the experimental verification of quantum mechanics principles, such as entanglement and the no-cloning theorem, and the technological challenges in performing these experiments with high precision.
- 🔄 The idea that entanglement can be seen as a form of correlation that is stronger than classical correlations is presented, where the result of measuring one particle seems to instantly determine the state of another, distant particle.
- 📓 The transcript concludes with a mention of entanglement entropy as a measure of the degree of entanglement between two systems, which is a concept that could be further explored in the context of information theory.
Q & A
What is the significance of the entangled state of two electrons in quantum mechanics?
-The entangled state of two electrons is significant because it demonstrates a fundamental aspect of quantum mechanics where the quantum states of two particles can be linked such that the state of one (spin up or down) instantly determines the state of the other, regardless of the distance between them. This is known as quantum entanglement.
What does it mean for two electrons to be in a linear superposition of states?
-A linear superposition of states means that the system can exist in multiple states at once, and the overall state is a sum (or 'superposition') of these possible states. In the context of the two electrons, this means the system can be in a state where one electron is up and the other is down, or vice versa, and these possibilities are superposed until a measurement is made.
How does the expectation value of the spin components relate to the entangled state of two electrons?
-In the entangled state being discussed, the expectation value of any component of the spin (Sigma 1, Sigma 2, or Sigma 3) for both electrons is zero. This implies that there is no preferred direction in which the spin is polarized, which is a unique characteristic of the entangled state and differs from the behavior of a single electron.
What is the role of the Sigma matrices in the entangled state of two electrons?
-The Sigma matrices (Sigma 1, Sigma 2, and Sigma 3) represent the action on the spin states of the electrons. They are used to describe how the spin state changes under various transformations. In the context of the entangled state, these matrices help to define the correlation between the spins of the two electrons.
Why are the states with a plus and a minus sign considered different in the entangled state?
-The plus and minus signs in the entangled state represent the relative spin orientation of the two electrons. A plus sign indicates that the spins are aligned (both up or both down), while a minus sign indicates that the spins are anti-aligned (one up and one down). These two states are different because measuring one spin in the first state will always yield the same result for the other spin, whereas in the second state, it will always yield the opposite result.
What is the concept of 'locality' in the context of the entangled state, and why is it important?
-Locality refers to the idea that physical processes occurring at one location do not depend on the properties of objects at other locations. In the context of entangled states, it is important because it ensures that the correlation between entangled particles does not allow for faster-than-light communication, thus preserving the principles of causality and special relativity.
What does Bell's theorem imply about the nature of reality and classical physics?
-Bell's theorem implies that no classical (i.e., non-quantum) theory can reproduce all of the predictions of quantum mechanics. Specifically, it shows that certain correlations between distant particles are possible in quantum mechanics that cannot be explained by any classical theory, thus suggesting that 'local hidden variable' theories that attempt to provide a classical explanation for quantum phenomena are insufficient.
What is the singlet state in quantum mechanics, and how does it differ from the triplet state?
-The singlet state is an entangled state of two particles (like electrons) where the total spin is zero. It is characterized by the property that the spins are always opposite when measured along the same axis. The triplet state, on the other hand, is a set of three states where the total spin is 1, and the individual spins can point in the same direction or in opposite directions. The singlet state exhibits stronger correlations between the particles than the triplet state.
How does the violation of Bell's inequality by quantum mechanics affect our understanding of the world?
-The violation of Bell's inequality by quantum mechanics demonstrates that the world cannot be described by classical physics alone. It suggests that 'spooky action at a distance', as Einstein called it, is a real phenomenon, where entangled particles can exhibit correlations that cannot be explained by local hidden variables. This has profound implications for our understanding of the fundamental nature of reality.
What is the no-cloning theorem in quantum mechanics, and why is it significant?
-The no-cloning theorem states that it is impossible to create an identical copy of an arbitrary unknown quantum state. This is significant because it implies that quantum information cannot be copied without altering the original state, which has implications for quantum computing and the potential for secure quantum communication.
What is entanglement entropy, and how is it related to the entangled state of two electrons?
-Entanglement entropy is a measure of the degree of entanglement between two quantum systems. It quantifies the amount of information that is shared between the two systems. In the context of two entangled electrons, entanglement entropy would be a measure of how much the state of one electron is dependent on the state of the other, reflecting the strength of their quantum correlation.
Outlines
📘 Introduction to Quantum Entanglement
The paragraph introduces the concept of quantum entanglement using the example of two entangled electrons. It explains the significance of the entangled state and the correlation between the spins of the electrons. The speaker also discusses the action of various Sigma operators on these states and emphasizes the importance of normalization in quantum mechanics.
📙 Expectation Values and Spin Correlations
This section delves into the expectation values of the spin components in entangled states. It is shown that the expectation value of any spin component results in zero, indicating no definite polarization direction. The paragraph also highlights the difference between entangled states and simple juxtapositions of individual spin states.
📗 The Action of Sigma Operators on Entangled States
The paragraph explores the effects of applying Sigma operators to the entangled states of two electrons. It is demonstrated that certain combinations of these operators yield zero, which is a key property of the entangled states. The discussion also touches on the concept of measuring the magnetic moment of the combined system.
📓 The Singlet and Triplet States
The distinction between singlet and triplet states is made in this paragraph. The singlet state is characterized by the property that the sum of the spins is always zero upon measurement, regardless of the direction. This leads to a strong correlation between the spins of the two particles, which is a fundamental aspect of quantum entanglement.
📒 Correlations and Einstein-Podolsky-Rosen Paradox
The paragraph discusses the profound nature of quantum correlations, often referred to as Einstein-Podolsky-Rosen (EPR) correlations. It is explained that measuring one spin instantly determines the other, despite the distance between them. The implications of this for causality and locality are also considered.
📔 Bell's Theorem and Classical Logic
The speaker introduces Bell's theorem, which is a classical theorem that quantum mechanics violates. It is emphasized that Bell's inequality is derived from classical logic and set theory, and its violation by quantum mechanics signifies the non-classical nature of quantum systems. The discussion also touches on the concept of causality and the fact that quantum mechanics does not violate it.
📒 Bell's Inequality in Quantum Systems
This paragraph focuses on applying Bell's inequality to a system of two spins, defining properties A, B, and C in the context of spin measurements. The violation of Bell's inequality in the quantum realm is highlighted, showing that quantum mechanics cannot be explained by classical logic alone.
📕 Projection Operators and Quantum Probabilities
The concept of projection operators is introduced as a tool for calculating probabilities in quantum mechanics. The paragraph explains how these operators correspond to certain propositions about a quantum system and how their expectation values can be used to determine the probability of a given outcome.
📔 Quantum Mechanics and No-Cloning Theorem
The no-cloning theorem is discussed, which states that it is impossible to create a machine that produces identical copies of an arbitrary unknown quantum state. The linearity of quantum mechanics and the tensor product of state vectors are key to understanding why cloning is not possible.
📘 Information Transfer vs. Cloning in Quantum Mechanics
The final paragraph distinguishes between transferring information from one quantum system to another and the concept of cloning. It is noted that while information can be transferred, the act of cloning, which implies creating two independent systems in the same state, is not possible according to the principles of quantum mechanics.
Mindmap
Keywords
💡Entanglement
💡Superposition
💡Spin
💡Normalization
💡Sigma Operators
💡Expectation Value
💡Singlet State
💡Triplet State
💡Bell's Theorem
💡Projection Operator
💡No Cloning Theorem
Highlights
Exploration of the difference a sign can make in an entangled state of two electrons, focusing on the correlation between their spins.
Discussion on the linear superposition of states and the significance of the plus or minus sign in entangled states.
Explanation of the action of various Sigma operators on the eigenstates of Sigma 3.
Analysis of the expectation value of any component of the spin in entangled states, revealing no definite polarization direction.
Insight into the concept of entangled states not being a simple juxtaposition of individual spin states.
Calculation and interpretation of the expectation value of Sigma 3 in a specific state, emphasizing its implications for measurement outcomes.
Investigation of the operator representing the sum of both spins and its action on entangled states.
Differentiation between the singlet and triplet states of two electrons, highlighting their unique properties and implications for quantum mechanics.
Introduction to Bell's theorem and its significance in quantum mechanics, including the violation of Bell's inequality.
Ambivalence about the profundity of Bell's theorem and its implications for the understanding of quantum mechanics.
Derivation of a classical theorem related to set theory that is used to establish a baseline for understanding quantum correlations.
Application of the classical theorem to a quantum system of two spins, leading to a contradiction with quantum mechanics predictions.
Discussion on the no-go theorem for cloning quantum states, known as the no-cloning theorem.
Proof that a universal quantum cloning machine is impossible due to the linearity of quantum mechanics.
Explanation of the tensor product and its role in combining state vectors of independent systems.
Illustration of the inconsistency that arises when trying to clone a quantum state that is a superposition of basis states.
Reflection on the difference in information content between independent entities and an entangled entity in quantum mechanics.
Introduction to the concept of entanglement entropy as a measure of the degree of entanglement between two systems.
Transcripts
Browse More Related Video

Lecture 4 | Quantum Entanglements, Part 1 (Stanford)

Spooky Action at a Distance (Bell's Inequality) - Sixty Symbols
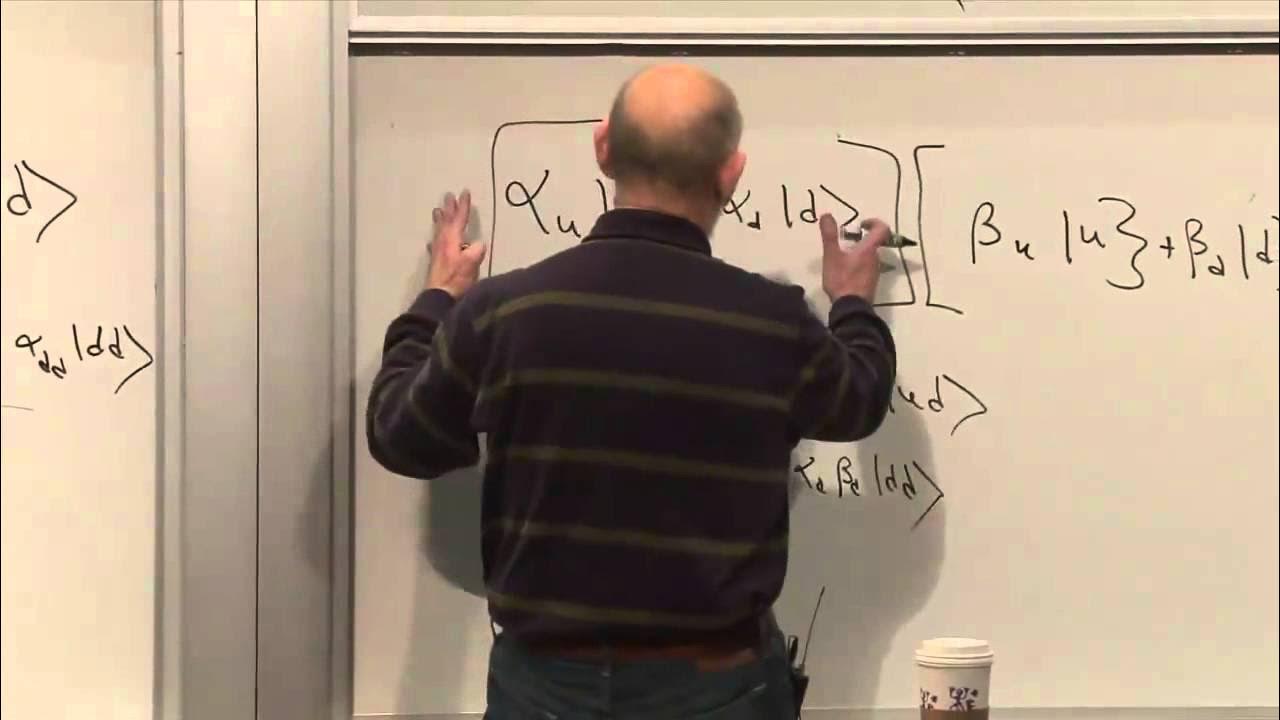
Lecture 6 | The Theoretical Minimum

Lecture 9 | Quantum Entanglements, Part 1 (Stanford)

Quantum Entanglement & Spooky Action at a Distance

Quantum Computing Expert Explains One Concept in 5 Levels of Difficulty | WIRED
5.0 / 5 (0 votes)
Thanks for rating: