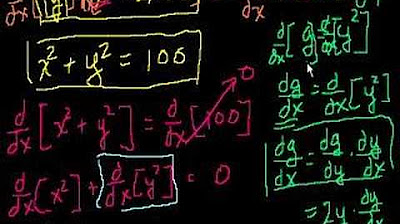Implicit Differentiation | Differentiation when you only have an equation, not an explicit function
TLDRThe transcript discusses the concept of implicit functions in calculus, contrasting them with explicit functions. The focus is on how to derive implicit functions, using the example of the equation of a circle, \(x^2 + y^2 = 1\). The speaker explains that while the circle equation does not define a single function \(y = f(x)\) due to the vertical line test, it can be split into two functions representing the top and bottom halves of the circle, \(y = \pm\sqrt{1 - x^2}\). The process of finding the derivative of \(y\) with respect to \(x\) is then detailed, applying the chain rule to the circle's equation. The derivative formula \(\frac{dy}{dx} = -\frac{x}{y}\) is derived and used to find the slope of the tangent line at specific points on the circle. The summary concludes with the evaluation of the derivative at a particular point, illustrating the concept of a vertical asymptote at the origin where the derivative is undefined due to division by zero.
Takeaways
- 📚 We've been studying explicit functions, where Y is given as a function of X, and we typically find the derivative f'(X).
- 🤔 Implicit functions are given by an equation involving both X and Y, and we want to determine if we can extract explicit functions from them.
- 🔍 The example given is the equation of a circle, x^2 + y^2 = 1, which naturally has multiple Y values for each X value.
- 🚫 The vertical line test shows that we cannot represent the entire circle with a single function Y = f(X) because it would require two Y values for a single X value.
- 📈 We can define two separate functions for the top and bottom semicircles using the positive and negative square roots from the circle's equation.
- 🧮 To find the derivative of Y with respect to X for an implicit function, we differentiate both sides of the equation with respect to X, applying the chain rule for composite functions.
- 💡 The general formula derived for the derivative dy/dx is -2x/(2y) or -x/y, keeping in mind that Y is a function of X.
- 📌 To find the slope of the tangent line at a particular point on the circle, we evaluate the derivative dy/dx at that point.
- 🔑 At the point (-1/√2, 1/√2), the slope of the tangent line is positive and equal to 1, indicating a specific direction for the tangent line.
- ⚠️ At the point where X = -1, we encounter a vertical asymptote because the derivative involves division by Y, which is 0 at this point.
- 🔁 The process can be repeated for any point on the circle to find the slope of the tangent line, providing insight into the behavior of the function at different points.
Q & A
What are explicit functions in calculus?
-Explicit functions in calculus are functions where the dependent variable, typically denoted as 'y', is given as some function of the independent variable 'x'. They are expressed in the form y = f(x).
What is the standard problem associated with explicit functions?
-The standard problem associated with explicit functions is to find the derivative of the function, often denoted as f'(x) or dy/dx, which represents the rate of change of the function with respect to x.
What is an implicit function and how is it different from an explicit function?
-An implicit function is a relationship between variables that is not expressed in explicit form (y = f(x)). Instead, it is given by an equation that involves both variables, such as x^2 + y^2 = 1. Unlike explicit functions, implicit functions do not isolate y as a function of x.
Why can't the equation x^2 + y^2 = 1 represent a single function y = f(x)?
-The equation x^2 + y^2 = 1 cannot represent a single function y = f(x) because for every value of x, there are two possible values of y (one positive and one negative) that satisfy the equation. This violates the vertical line test, which states that a function must pass through exactly one point for every vertical line drawn on the graph.
How can the circle equation x^2 + y^2 = 1 be represented by two explicit functions?
-The circle equation can be represented by two explicit functions by considering the positive and negative square roots of (1 - x^2). This gives two functions: y = sqrt(1 - x^2) for the upper semicircle and y = -sqrt(1 - x^2) for the lower semicircle.
What is the derivative of y with respect to x for an implicit function?
-To find the derivative of y with respect to x for an implicit function, you can differentiate both sides of the equation with respect to x using the chain rule. For the circle equation, the derivative dy/dx is given by -2x/(2y) or -x/y.
What is the slope of the tangent line to the circle at the point (-1/√2, 1/√2)?
-The slope of the tangent line to the circle at the point (-1/√2, 1/√2) is found by evaluating the derivative dy/dx at that point, which results in a slope of 1.
What happens to the derivative dy/dx at the point (-1, 0) on the circle?
-At the point (-1, 0) on the circle, the derivative dy/dx results in a division by zero, indicating a vertical asymptote. This means the slope of the tangent line is undefined at this point.
What is the significance of the vertical line test in the context of functions?
-The vertical line test is a graphical method to determine if a curve represents a function. If any vertical line intersects the curve at more than one point, then the curve does not represent a function because a function requires each x-value to correspond to exactly one y-value.
How can you find the derivative of an implicit function without explicitly solving for y as a function of x?
-You can find the derivative of an implicit function without explicitly solving for y as a function of x by applying the chain rule to differentiate both sides of the implicit equation with respect to x. This allows you to express dy/dx in terms of x and y.
What is the role of the chain rule in differentiating an implicit function?
-The chain rule is used when differentiating an implicit function to handle the composition of functions, such as y^2, where y is a function of x. It allows you to differentiate the outer function (squaring in this case) with respect to the inner function (y as a function of x).
How does the concept of a tangent line relate to the derivative of a function?
-The derivative of a function at a particular point gives the slope of the tangent line to the graph of the function at that point. It represents the instantaneous rate of change of the function at that point.
Outlines
📚 Understanding Implicit Functions and Their Derivatives
The video script begins by discussing explicit functions, where 'y' is given as a function of 'x', and the common task of finding the derivative, denoted as f'(x). It then transitions to implicit functions, which are not explicitly given as y=f(x), using the example of the equation x^2 + y^2 = 1, which represents a circle. The script explores the challenge of finding explicit functions from an implicit equation and demonstrates that the circle equation results in two functions due to the positive and negative square roots of (1-x^2). These correspond to the top and bottom semicircles, respectively. The video also delves into the concept of the derivative of y with respect to x in the context of implicit differentiation, leading to the formula dy/dx = -2x/(2y) or -x/y. It concludes with a note on the conventional notation of omitting the 'x' in function references while still applying the chain rule.
🔍 Evaluating Derivatives at Specific Points
The second paragraph focuses on applying the previously derived formula for the derivative to find the slope of the tangent line at specific points on the circle. It uses the point (-1/√2, 1/√2) as an example to demonstrate the process of evaluating the derivative at a given point. The script shows that the slope of the tangent line at this point is 1, indicating a steep incline. Additionally, it addresses what happens when the derivative is evaluated at points where the denominator becomes zero, such as (-1, 0), resulting in a vertical asymptote. The video concludes by plotting the tangent line at the given point and noting the implications of the derivative at points of vertical tangency.
Mindmap
Keywords
💡Explicit functions
💡Implicit functions
💡Derivative
💡Chain rule
💡Vertical line test
💡
💡Tangent line
💡Square root
💡Circle equation
💡Asymptote
💡Slope
💡Graph
Highlights
Calculus has focused on explicit functions, where Y is given as a function of X.
Implicit functions are naturally given but require explicit functions to be derived from them.
The equation x^2 + y^2 = 1 is an example of an implicit function representing a circle.
For every value of x, there may be multiple y values satisfying the equation, leading to the concept of semicircles as separate functions.
The vertical line test is used to determine if an equation can represent a single function.
Two explicit functions can be derived from the circle equation, one for the top semicircle and one for the bottom.
The derivative of Y with respect to X can be found using the chain rule for composite functions.
The derivative dy/dx is expressed as -2x/2y or -x/y, which is a systematic way to compute the derivative for implicit functions.
Different parts of the circle (top and bottom semicircles) correspond to different derivatives based on the positive or negative square root.
The slope of the tangent line at a particular point on the circle can be found using the derivative dy/dx.
The point (-1/√2, 1/√2) on the circle has a positive slope of 1 for its tangent line.
The point (-1, 0) on the circle represents a vertical asymptote where the slope of the tangent line is undefined.
The process of finding derivatives for implicit functions involves rearranging the equation and applying the chain rule.
The notation Y of X is used to denote that Y is implicitly dependent on X, even when not explicitly written.
The derivative dy/dx is evaluated at specific points on the circle to find the slope of the tangent line at those points.
The concept of the chain rule is crucial for differentiating composite functions in calculus.
The circle equation x^2 + y^2 = 1 serves as a practical example to illustrate the process of finding derivatives for implicit functions.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: