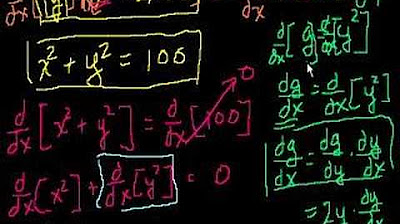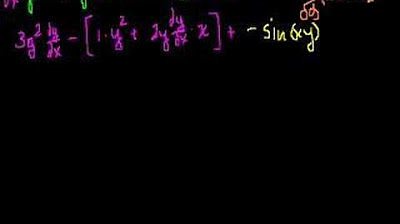Implicit Differentiation - Vertical and Horizontal Tangents

turksvids
21 Sept 201305:44
EducationalLearning
32 Likes 10 Comments

TLDRThe video script presents a comprehensive tutorial on implicit differentiation, a method used to find the derivative of y with respect to x in equations where y is implicitly defined. The example given is x^2 + xy + y^2 = 4. The process involves differentiating both sides of the equation with respect to x, applying the chain rule for the product and quotient of functions, and rearranging terms to solve for dy/dx. The video also addresses common mistakes such as forgetting to apply the chain rule and the derivative of a constant being zero. Further, it explores scenarios where the slope of the curve is zero or undefined, leading to solving for x and y to find specific points on the curve. The tutorial concludes with a GeoGebra demonstration, confirming the horizontal and vertical tangent lines at points A, B, C, and D, offering a visual aid to reinforce the concepts taught.

Takeaways
  • 📚 Start by differentiating both sides of the given equation with respect to x to find dy/dx.
  • 🔍 Use the product rule for the term XY and the chain rule for y^2 since y is a function of x.
  • 🧩 Remember that the derivative of a constant is zero, which simplifies the differentiation process.
  • 📉 Move all terms without dy/dx to one side to isolate and factor out dy/dx.
  • 🔑 Solve for dy/dx by dividing through by the factored quantity to get the derivative expression.
  • 🔍 To find where the slope is zero, set dy/dx equal to zero and solve for x and y.
  • 🔗 Use the original equation to substitute and solve for x and y when the slope is zero.
  • 📐 Substitute the found values of x and y into the original equation to find the points where the slope is zero.
  • 🚫 Identify when the slope is undefined by setting the denominator of the dy/dx expression to zero and solving for x and y.
  • 🔢 Substitute the found x values into the original equation to find the corresponding y values for undefined slope points.
  • 📈 Use a tool like GeoGebra to graph the curve and verify the points where the slope is zero or undefined.
Q & A

  • What is the first step in implicitly differentiating the given equation x^2 + xy + y^2 = 4?

    -The first step is to take the derivative with respect to x of both sides of the equation.

  • When differentiating the term xy in the equation, what are the two components considered?

    -The two components are the derivative of the first term (x) times the second term (y), and the derivative of the second term (y) times the first term (x).

  • What is the derivative of a constant with respect to x?

    -The derivative of a constant with respect to x is 0.

  • How is the chain rule applied when differentiating y^2 in the given equation?

    -The chain rule is applied by taking the derivative of y^2 as 2y and then multiplying it by the derivative of y with respect to x, which is dy/dx.

  • What is the process for finding when the slope of the curve is zero?

    -To find when the slope of the curve is zero, set dy/dx equal to 0 and solve for x and y using the given equation and the derived dy/dx expression.

  • What is the relationship between x and y when the slope of the curve is zero?

    -When the slope is zero, the relationship between x and y is found by setting the numerator of the dy/dx expression to zero and solving the resulting equation.

  • How are the coordinates of the points where the tangent line is horizontal found?

    -The coordinates are found by substituting y = -2x into the original equation, simplifying, and solving for x and y to get the points (x, y).

  • What is the condition for the slope of the curve to be undefined?

    -The slope of the curve is undefined when the denominator of the dy/dx expression equals 0.

  • How are the points on the curve where the slope is undefined found?

    -The points are found by setting the denominator of the dy/dx expression to zero, solving for x and y, and then substituting these values back into the original equation.

  • What tool was used to confirm the results of the implicit differentiation?

    -GeoGebra was used to implicitly define the curve, find intersection points, and plot lines through those points to confirm the results.

  • What are the coordinates of the points where the tangent line is vertical (slope is undefined) on the curve?

    -The coordinates are found by substituting x + 2y = 0 into the original equation, solving for x and y, and getting the points (±4/√3, ±2/√3).

  • How does the process of implicit differentiation help in understanding the behavior of the curve?

    -Implicit differentiation allows us to find the slope of the curve at any point, which helps in understanding the tangent behavior, including where the slope is zero (horizontal tangents) and where it is undefined (vertical tangents).

Outlines
00:00
📚 Implicit Differentiation and Slope Analysis

This paragraph delves into the process of implicit differentiation, using the equation x^2 + XY + y^2 = 4 as an example. The speaker begins by differentiating both sides of the equation with respect to X, applying the chain rule for the product and the constant multiple rule. They then isolate dy/dx, factor it out, and solve for dy/dx to find the slope of the curve. The discussion continues with determining when the slope is zero by setting dy/dx to zero and solving for x and y, which gives the points where the tangent line is horizontal. The process is further explained by substituting y = -2x into the original equation to find the x and y coordinates of these points. Lastly, the speaker addresses when the slope of the curve is undefined, which occurs when the denominator of the fraction representing dy/dx is zero. The paragraph concludes with a mention of using a geogebra screenshot to illustrate the process.

05:01
📈 Geogebra Visualization of Implicitly Defined Curves

The second paragraph discusses the use of Geogebra to graph the implicitly defined curve from the first paragraph. The speaker describes a method where they graph y = -2x, find the intersection points, and then plot lines through these points. They also mention an alternative approach where y = -x/2 is graphed and intersection points are used to plot lines. The paragraph emphasizes confirming the slope analysis conducted earlier: the slope is zero at points A and B (horizontal tangent lines), and undefined at points C and D (vertical tangent lines). This visual approach aids in understanding the behavior of the curve and the concept of implicit differentiation.

Mindmap
Keywords
💡Implicit Differentiation
Implicit differentiation is a method used to find the derivative of an equation that is not explicitly solved for y. It is a crucial technique when dealing with equations where y is implicitly defined as a function of x. In the video, it is used to find dy/dx for the given equation x^2 + xy + y^2 = 4, which is not explicitly solvable for y in terms of x.
💡Derivative
A derivative in calculus represents the rate at which a quantity changes with respect to another quantity. In the context of the video, the derivative is used to find the rate of change of y with respect to x (dy/dx), which is essential for understanding the slope of the tangent line to the curve at any given point.
💡Chain Rule
The chain rule is a fundamental theorem in calculus for finding the derivative of a composite function. In the video, it is applied when differentiating y^2, where y is a function of x, resulting in 2y * (dy/dx). This rule is critical for handling the product of variables and functions within the implicit differentiation process.
💡Slope of the Curve
The slope of the curve, or dy/dx, indicates how steep the curve is at a particular point. In the video, finding when the slope is zero (dy/dx = 0) helps identify points where the tangent line to the curve is horizontal. This is important for understanding the behavior of the curve and its critical points.
💡Tangent Line
A tangent line is a straight line that touches a curve at a single point without crossing it. It is used to approximate the curve near that point. In the script, finding points where the tangent line is horizontal (slope is 0) or vertical (slope is undefined) is a key part of analyzing the curve defined by the equation.
💡Constant
In calculus, the derivative of a constant is always zero because a constant does not change with respect to the variable. In the video, when differentiating the constant 4 in the equation, it is noted that its derivative is 0, which simplifies the equation and helps in solving for dy/dx.
💡System of Equations
A system of equations is a set of two or more equations involving the same variables. In the video, after finding dy/dx = 0, the presenter uses a system of equations to find the corresponding x and y values for points where the slope is zero. This involves substituting y = -2x into the original equation to solve for x and y.
💡Geogebra
Geogebra is a mathematical software tool that allows for the creation of graphs and geometric constructions. In the video, it is used to visualize the curve defined by the equation and to confirm the points where the slope is zero or undefined by plotting lines through the intersection points of y = -2x and y = -x/2 with the curve.
💡Intersection Points
Intersection points are the points where two or more curves or lines meet. In the context of the video, finding the intersection points of the curve with lines y = -2x and y = -x/2 helps in identifying the points where the slope of the curve is zero or undefined.
💡Undefined Slope
An undefined slope occurs when the denominator of a fraction, which represents the slope, is zero. In the video, the presenter seeks to find when the slope of the curve is undefined by setting the denominator of the dy/dx expression (X + 2Y) to zero and solving for x and y.
💡Simplify
Simplification in mathematics involves reducing an expression to a more straightforward form while maintaining its value. In the video, the presenter emphasizes the importance of simplifying the equation after applying the chain rule and implicit differentiation to make it easier to solve for dy/dx and find the critical points of the curve.
Highlights

The process involves implicit differentiation of the equation x^2 + XY + y^2 = 4.

Derivative of x^2 is 2x, using basic differentiation rules.

Applying the product rule to differentiate XY, resulting in x(dy/dx) + y.

Using the chain rule to differentiate y^2, considering y as a function of x, leading to 2y(dy/dx).

Noting that the derivative of a constant is 0, simplifying the differentiation process.

Rearranging terms to isolate dy/dx and factoring it out to solve for dy/dx.

Finding when the slope dy/dx is equal to 0 by setting the numerator to zero.

Solving for x and y when the slope is zero using the original equation.

Identifying points on the curve where the tangent line is horizontal by substituting y = -2x.

Calculating the x and y coordinates of the points where the slope is zero.

Determining when the slope of the curve is undefined by setting the denominator to zero.

Solving for x and y when the slope is undefined using the original equation and y = -x/2.

Graphically representing the curve and its points of horizontal and vertical tangent lines using GeoGebra.

Confirming the theoretical findings with a visual representation in GeoGebra.

Highlighting the importance of understanding the chain rule and derivatives of constants in implicit differentiation.

Demonstrating the methodical approach to solving differential equations and finding specific points on a curve.

Providing a comprehensive walkthrough that bridges theoretical calculus with practical problem-solving.

Using substitution and simplification techniques to find exact coordinates of points of interest on the curve.

Combining algebraic manipulation with geometric interpretation to enhance understanding of the curve's properties.

Transcripts

Browse More Related Video

Implicit Differentiation

Implicit Differentiation | Differentiation when you only have an equation, not an explicit function

Implicit Differentiation

Math1325 Lecture 11 3 - Implicit Differentiation

Implicit Differentiation - Find The First & Second Derivatives

Implicit Differentiation (part 2)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Implicit DifferentiationMathematics TutorialDerivative CalculationSlope AnalysisEquation SolvingChain RuleGeometry ConceptsEducational ContentMath ProblemGeogebra ToolLearning Resource