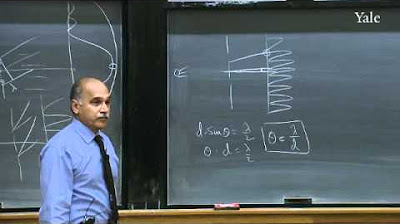Lecture 1 | Modern Physics: Quantum Mechanics (Stanford)
TLDRThe transcript appears to be a lecture from Stanford University, focusing on the fundamental concepts of quantum mechanics in the context of continuing education. The lecturer addresses the curious nature of quantum mechanics, contrasting it with classical mechanics and emphasizing the statistical and non-deterministic behavior inherent in quantum systems. Key phenomena such as quantum entanglement and the two-slit experiment are mentioned to illustrate the peculiarities of quantum physics. The lecture aims to provide a basic understanding of these concepts to an audience that may not be standard undergraduate or graduate students, suggesting that the content is tailored for a more general audience with a keen interest in theoretical physics. The lecturer also discusses the age distribution of the attendees, indicating a diverse group interested in learning the basic ideas of quantum mechanics quickly and efficiently.
Takeaways
- 🎓 The class is a part of Stanford University's Continuing Education program, aimed at individuals who are often older than traditional students and are interested in theoretical physics at a full scale level.
- 🌐 The course material is available on the internet and is designed to be self-contained, covering advanced topics in quantum mechanics, which is different from standard undergraduate or graduate courses.
- 👥 The audience consists of people from various backgrounds, not just Stanford affiliates, and includes participants from the local community and even those located further away.
- 📈 The age distribution of the attendees ranges from under 40 to over 90, indicating a diverse and mature student body that is eager to grasp complex concepts quickly.
- 🧮 The teaching approach focuses on using the simplest equations necessary to explain phenomena, aiming for minimalism and efficiency in conveying the fundamentals of quantum mechanics.
- 🚀 The course is a part of a series that began with classical mechanics and progresses to more complex topics such as quantum entanglement, with each course building on the previous one.
- 🌟 Quantum mechanics introduces statistical thinking and an element of unpredictability or indeterminacy that is not present in classical mechanics.
- 📉 The concept of energy conservation remains a fundamental principle in quantum mechanics, even when systems exhibit unpredictable behavior.
- 🤔 The famous quote by Einstein, "God does not play dice," and Niels Bohr's response highlight the philosophical debate about the nature of reality as described by quantum mechanics.
- 👻 The two-slit experiment is highlighted as a classic demonstration of the peculiar nature of quantum mechanics, where the act of observation affects the outcome, a phenomenon with no classical counterpart.
- ⚖️ The Heisenberg Uncertainty Principle is introduced as a fundamental aspect of quantum mechanics, which places a limit on the precision with which certain pairs of physical properties, like position and momentum, can be known.
Q & A
What is the main focus of the class being discussed in the transcript?
-The class focuses on theoretical physics, specifically quantum mechanics, at a full scale level. It is designed for a mature audience, including those who are not traditional students, and aims to teach the basics of quantum mechanics in a straightforward and efficient manner.
Why are people from Europe curious about the class?
-People from Europe, particularly physicists following the class online, are curious because the class does not seem like a standard undergraduate or graduate course. They sense that the teaching method and content are different and are interested in the nature of the class and the background of the attendees.
What is the age distribution of the attendees in the class?
-The age distribution is quite varied, with a handful of people under 40 and a significant number over 70, including some over 80 and even a few over 90. This indicates that the class attracts a wide range of ages, all interested in understanding quantum mechanics.
What is the educational background of the attendees?
-While some attendees might be affiliated with Stanford University as employees or past students, the majority are from the community and are considered too old to be traditional undergraduate or graduate students.
How does the class approach the teaching of quantum mechanics?
-The class aims to use the simplest equations necessary to explain concepts, maintaining a focus on minimalism. It emphasizes the importance of understanding the basic ideas quickly and efficiently, even if those ideas are more difficult or elaborate.
What is the significance of the two-slit experiment in quantum mechanics?
-The two-slit experiment is significant because it demonstrates the wave-particle duality of quantum mechanics. It shows how particles like electrons can display interference patterns that cannot be explained by classical mechanics, highlighting the fundamentally different logic of quantum physics.
What is the role of statistics and randomness in quantum mechanics?
-Statistics and randomness are central to quantum mechanics. Unlike classical mechanics, where randomness might be introduced in a way that affects both position and momentum, quantum mechanics has an inherent, non-deterministic nature where the outcome of measurements is probabilistic and can lead to phenomena like the conservation of energy despite apparent randomness.
Why is the concept of reversibility important in understanding the laws of physics?
-Reversibility is important because it relates to the idea that the laws of physics are deterministic. If the laws of physics could be reversed, a system would return to its original state after a certain time, indicating that information is conserved and the system's evolution is predictable.
What is the Heisenberg Uncertainty Principle, and how does it apply to quantum mechanics?
-The Heisenberg Uncertainty Principle states that it is impossible to simultaneously measure the position and momentum of a particle with absolute precision. The more precisely one property is measured, the less precisely the other can be known. This principle is a fundamental aspect of quantum mechanics that highlights the limitations of our ability to know a system's state completely.
How does the concept of a vector space relate to the states in quantum mechanics?
-In quantum mechanics, the state of a system is represented by a vector in a vector space, which is a mathematical structure that allows for the addition of vectors and multiplication by scalars (complex numbers in this case). This is a departure from classical mechanics, where states are represented by points in a phase space.
What is the difference between a bra vector and a ket vector in the context of quantum mechanics?
-Bra and ket vectors are two different kinds of vectors used in quantum mechanics. A ket vector is used to represent the state of a quantum system, while a bra vector is the complex conjugate transpose of a ket vector. When a bra and a ket are multiplied together, they form a bracket, which is used to calculate the expected values of observables.
Outlines
😀 Introduction to Stanford's Continuing Education Program
The speaker introduces the educational program at Stanford University, highlighting its focus on continuing education for non-traditional students. The class is not a standard undergraduate or graduate course but aims to deliver theoretical physics at a full scale level. The speaker addresses the curiosity of European physicists about the nature of the class and clarifies that it is designed for adults from the community, including those over 70 and even over 90, who are eager to grasp fundamental concepts efficiently and quickly.
📚 Course Outline and Quantum Mechanics Basics
The lecturer outlines the series of courses, emphasizing that the current class is on quantum mechanics, following an initial course on classical mechanics. The explanation delves into the statistical nature of quantum mechanics, contrasting it with classical physics. The speaker criticizes a deterministic approach to physics, alluding to Einstein's famous quote about God not playing dice, and introduces the concept of quantum entanglement as a fundamental aspect of the course.
🚀 The Special Nature of Quantum Randomness
The discussion focuses on the unique randomness inherent in quantum mechanics, differentiating it from classical randomness. The lecturer uses the illustration of a deity throwing dice to modify Newton's laws, suggesting that while this introduces unpredictability, it does not replicate quantum mechanics' peculiar brand of unpredictability. The conservation of energy in quantum mechanics, despite its inherent unpredictability, is emphasized, setting the stage for a deeper exploration of quantum phenomena.
🧲 The Two-Slit Experiment & Quantum Weirdness
The lecturer introduces the two-slit experiment to demonstrate the odd behavior in quantum physics, contrasting it with classical randomness. The experiment involves particles like photons, electrons, or neutrons passing through two slits and creating an interference pattern on a screen. The speaker explains how this pattern defies classical expectations and introduces the concept of destructive interference, which is a fundamental aspect of quantum mechanics that challenges classical logic.
🔄 Reversibility and the Loss of Information in Physics
The concept of reversibility in physics is explored, where the lecturer discusses deterministic laws and the idea of reversing the laws of physics to test for information loss. It is explained that in classical mechanics, information is conserved, and the system returns to its original state after being reversed. However, the introduction of classical randomness leads to a loss of this conservation. The lecturer then ponders whether information is lost in quantum mechanics, setting up a comparison that will be explored further in the lecture.
🎯 Quantum Mechanics and the Heisenberg Uncertainty Principle
The Heisenberg Uncertainty Principle is introduced as a fundamental concept in quantum mechanics that sets it apart from classical physics. The principle implies a limit to the precision with which pairs of physical properties, like position and momentum, can be known. The lecturer illustrates this with the idea of measuring an electron's position with a photon, explaining how the act of measurement affects the electron's momentum, thus introducing uncertainty.
🤔 The Intrinsic Disturbance in Quantum Measurement
The lecturer delves into the idea that measurement in quantum mechanics is inherently disturbing, contrasting it with classical physics where measurement can be arbitrarily gentle. The text discusses how observing a quantum system, such as an electron, during an experiment can drastically change the outcome, as opposed to classical systems that can be observed without significant disturbance. The uncertainty principle is highlighted as a key factor that prevents the simultaneous precise measurement of position and momentum.
📐 The Mathematical Framework of Quantum States
The lecturer shifts the discussion towards the mathematical representation of quantum states, emphasizing that states in quantum mechanics are not points in a set but vectors in a vector space. This vector space is over the complex numbers, distinguishing it from classical mechanics that operates on set theory. The speaker introduces the concept of a Hilbert space, a vector space that will be central to understanding quantum mechanics, and contrasts it with the classical notion of a phase space.
🔍 Complex Numbers, Vector Spaces, and Quantum States
The discussion continues with the properties of vector spaces over the complex numbers, including the ability to multiply vectors by complex numbers and to add vectors to form new vectors. The lecturer provides examples of vector spaces, such as complex functions and column vectors, and explains the rules for their manipulation. The abstract nature of these mathematical constructs is emphasized as a foundational aspect of quantum mechanics, which will be applied to describe quantum systems.
🏷️ Dual Vector Spaces and Quantum Mechanics
The lecturer concludes the segment by introducing the concept of a dual vector space, which is in one-to-one correspondence with the original vector space. The importance of complex conjugation in the context of complex numbers is also highlighted. The speaker notes that the mathematical framework presented is essential for understanding quantum mechanics and that future sessions will apply these concepts to quantum mechanical problems.
Mindmap
Keywords
💡Continuing Education
💡Theoretical Physics
💡Quantum Mechanics
💡Indeterminism
💡Two-Slit Experiment
💡Wave-Particle Duality
💡Heisenberg's Uncertainty Principle
💡Complex Numbers
💡Vector Space (Hilbert Space)
💡State Vector
💡Complex Conjugation
Highlights
The class is a part of Continuing Education at Stanford University, designed for individuals not necessarily from Stanford but from the community, focusing on theoretical physics.
The course material is not standard undergraduate or graduate physics but dives into real McCoy theoretical physics using the simplest equations to explain concepts.
The age distribution of the class is diverse, with attendees ranging from under 40 to over 90, indicating a broad interest in the subject across different age groups.
The teaching approach aims to convey the basic ideas quickly and efficiently, using equations and minimal elaboration to ensure understanding.
The course is a series of about six ten-lecture series, starting with classical mechanics and moving on to quantum mechanics, including a focus on quantum entanglement.
Quantum mechanics is fundamentally different from classical physics, particularly in its introduction of statistical thinking and unpredictability.
The famous quote by Einstein, "God does not play dice," is discussed, contrasting with Niels Bohr's response that we should not tell God what to do.
The two-slit experiment is introduced as a straightforward demonstration of the peculiarities of quantum mechanics compared to classical randomness.
The concept of reversibility in physics is explored, highlighting the difference between classical and quantum mechanics regarding the conservation of information.
The Heisenberg Uncertainty Principle is mentioned, which fundamentally restricts the ability to simultaneously measure the position and momentum of a particle.
The use of complex numbers and vector spaces in quantum mechanics is emphasized, contrasting with the set theory used in classical mechanics.
The state of a quantum system is represented by a vector in a vector space, a radical departure from classical mechanics where states are points in a set.
The course aims to not only understand the differences between classical and quantum mechanics but also to learn how to apply quantum mechanics to calculations.
The mathematical framework of quantum mechanics, including the use of complex functions and column vectors, is introduced as fundamental to the subject.
The concept of a dual vector space and the importance of complex conjugation in the context of quantum mechanics are discussed.
The program is copyrighted by Stanford University, emphasizing the academic and intellectual property of the course material presented.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: