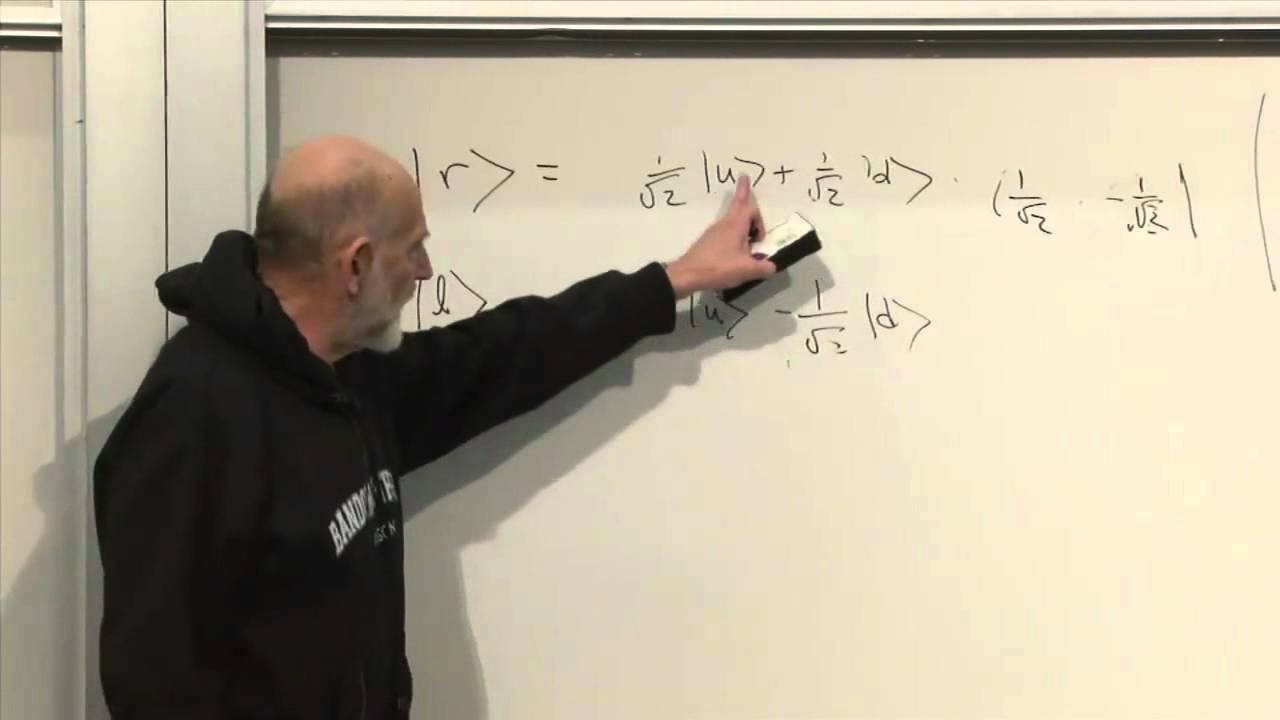Lecture 1 | The Theoretical Minimum
TLDRThe video script is an in-depth exploration of classical and quantum mechanics, contrasting the intuitive nature of classical mechanics with the abstract and often counterintuitive principles of quantum mechanics. It delves into the concept of a system's state, emphasizing the deterministic nature of classical physics and the probabilistic and non-intuitive nature of quantum states. The script introduces the qubit, a quantum analog of the classical bit, to illustrate the superposition and directionality inherent in quantum systems. It also discusses the role of the measuring apparatus in quantum mechanics and how measurement affects the state of a quantum system, a phenomenon that has no parallel in classical physics. The lecturer further explains the mathematical framework of vector spaces and inner products, which are essential for understanding the space of states in quantum mechanics. The summary underscores the fundamental differences in the logic of set theory versus vector spaces and the importance of abstract mathematics in describing quantum phenomena that cannot be visualized with conventional intuition.
Takeaways
- 📚 Classical mechanics is based on intuitive concepts that can be visualized, such as the motion of particles and objects, but becomes abstract with increased complexity.
- 🌟 The French contribution to classical mechanics introduced mathematical elegance through concepts like Lagrangians and Poisson brackets, which are crucial for understanding the subject.
- 🔍 Classical mechanics is deterministic and predictive, focusing on the concept of a system's state, which is a collection of different states that the system can be in.
- 🧠 Moving beyond classical physics into quantum mechanics or relativity involves dealing with concepts that are beyond everyday human intuition and require abstract mathematical descriptions.
- 🚫 Direct visualization of quantum phenomena is not possible for humans due to our neural architecture being hardwired for three-dimensional understanding.
- ⚖️ The logic of quantum mechanics is different from classical logic, with quantum states not being part of a set in the same way as classical states.
- 🎯 Quantum mechanics introduces the concept of a qubit, which, like a coin, has two states but is more complex and has a sense of directionality in space.
- 🔄 The act of measuring in quantum mechanics can be seen as a preparation of the system into a particular state, with the apparatus (detector) playing a crucial role in the process.
- ↕️ A qubit, upon measurement, yields a random result of plus or minus one, but once a state is found, subsequent measurements along the same axis will yield the same result until a change is made.
- 🔀 The orientation of the measuring apparatus (detector) relative to the qubit affects the outcome of the measurement, suggesting that qubits have spatial directionality.
- 📈 The average value of the horizontal component of a qubit, when measured in a large number of trials, is zero, reflecting the probabilistic nature of quantum states.
Q & A
What is classical mechanics?
-Classical mechanics is a branch of physics that deals with the motion of particles and objects based on concepts drawn from the everyday world. It is intuitive and deterministic, allowing for the prediction of the system's evolution given its state at a specific time.
What is the concept of a space of states in classical mechanics?
-The space of states in classical mechanics refers to the collection of all possible configurations that a system can have. It is a mathematical set that describes the different states a system can be in.
How does the concept of a system in classical mechanics differ from quantum mechanics?
-In classical mechanics, a system is a closed, isolated entity whose motion and evolution can be predicted without interaction with anything else. In quantum mechanics, the concept of a system is more abstract and involves states that are not as easily definable or isolated.
What is a qubit?
-A qubit, short for quantum bit, is the basic unit of quantum information. It is a system that can be in a superposition of two states, often represented as 'heads' and 'tails' or '+'1 and '-1', and exhibits properties that are fundamentally different from classical bits.
What is the significance of the detector's orientation in a quantum mechanics experiment?
-The orientation of the detector is significant because it determines the axis along which the qubit's state is measured. The detector's orientation can affect the outcome of a measurement, indicating that qubits have a sense of directionality in space.
How does the act of measurement in quantum mechanics affect the state of a qubit?
-Measurement in quantum mechanics causes the qubit to collapse into one of its definite states. This process not only determines the state of the qubit at the moment of measurement but also 'prepares' the qubit in that state for subsequent measurements.
What is the concept of an apparatus in quantum mechanics?
-An apparatus in quantum mechanics is a device used to measure or interact with a quantum system. It is considered a black box that can register outcomes based on its interaction with the system, and its role is crucial in quantum experiments.
Why is it difficult to visualize concepts beyond classical physics, such as quantum mechanics or relativity?
-It is difficult to visualize concepts beyond classical physics because they deal with parameters and phenomena that are outside the realm of ordinary experience, such as very small objects, high velocities, or higher dimensions. Our brains are not wired to visualize such abstract concepts directly, requiring the use of abstract mathematics to describe and understand them.
What is the role of mathematics in describing physical phenomena that cannot be visualized?
-Mathematics provides a language and framework to describe and understand physical phenomena that cannot be visualized. It allows physicists to model, predict, and analyze the behavior of systems even when they cannot be directly observed or imagined.
How is the logic of quantum mechanics different from the logic of classical mechanics?
-The logic of quantum mechanics is different because it does not rely on the concept of a system's state being a member of a mathematical set. Instead, it involves vector spaces and the superposition of states, which are fundamentally different from the discrete states in classical mechanics.
What is the phase space in classical mechanics?
-Phase space in classical mechanics is a space consisting of all possible states of a system. For a particle moving on a line, the phase space is a plane with one axis representing position (q) and the other representing momentum (p), where each point in the plane represents a possible state of the particle.
How does the concept of 'and' and 'or' apply to sets of states in classical logic?
-In classical logic, 'and' corresponds to the intersection of sets, meaning it represents the common elements between two sets of states. 'Or' corresponds to the union of sets, encompassing all elements from both sets, with the possibility of including elements that are present in either set.
Outlines
📚 Introduction to Classical Mechanics
The paragraph introduces classical mechanics, emphasizing its intuitive nature based on everyday concepts like particle motion. It discusses the evolution of classical mechanics with the French focus on mathematical elegance, leading to the development of Lagrangians and other abstract concepts. The importance of understanding the state of a system and its predictability is highlighted, using simple examples like a coin toss to illustrate the concept of state space.
🌐 Visualization Challenges in Physics
This paragraph addresses the limitations of visualization in physics, particularly when dealing with phenomena beyond ordinary experience. It stresses the inability to visualize high-speed particles or higher dimensions and the necessity of abstract mathematical descriptions. The paragraph warns against relying on intuition for understanding complex physical concepts and emphasizes the importance of abstract thinking and mathematics.
🧮 Quantum Mechanics and Abstract States
The paragraph delves into the abstract nature of quantum mechanics, contrasting it with classical mechanics. It introduces the concept of a quantum system's state, which is not a simple set but a vector space. The paragraph explains the idea of a system and its states, using the example of a die to illustrate the space of states. It also touches upon the logic of quantum mechanics, which is fundamentally different from classical logic.
🤔 Logic in Classical and Quantum Physics
This paragraph explores the logical concepts in classical physics, such as 'and', 'or', and the use of set theory to describe system states. It contrasts this with quantum mechanics, where the logic is not based on set theory but on vector spaces. The paragraph also introduces the concept of a qubit, the quantum analog of a classical bit, and its two states, heads and tails, represented mathematically as +1 and -1.
🔬 The Quantum Experiment and Measurement
The paragraph discusses the concept of an experiment in quantum mechanics, involving a system and an apparatus. It explains the process of measurement and how it can be seen as a preparation of the system in a certain state. The paragraph highlights the deterministic nature of quantum mechanics, where repeated measurements yield the same result, and introduces the idea of a quantum system having a sense of directionality.
🧲 Directionality and Vector Nature of Qubits
This paragraph investigates the directionality and vector nature of qubits through experiments. It describes how changing the orientation of the detector affects the measurement outcome, suggesting that qubits have spatial directionality. The paragraph also touches on the idea that a detector might be measuring the component of a vector along its direction and the implications of this for understanding quantum states.
🎰 Randomness and Confirmation in Quantum Experiments
The paragraph explores the concept of randomness in quantum mechanics, where individual measurements of a quantum system yield random outcomes, but the average over many measurements is predictable. It discusses the idea of confirming experiments in quantum mechanics and the role of the apparatus in determining the state of a system. The text also addresses the memory of the detector and the concept of a qubit's state being prepared by observation.
📈 Average Values and Vector Components
This paragraph focuses on the idea that average values of measurements in quantum mechanics behave as if they were components of a vector. It discusses the outcome of measurements when the detector is rotated by various angles and how these outcomes relate to the cosine of the angle, drawing parallels with classical vector components. The paragraph emphasizes the statistical nature of quantum measurements and the concept of a qubit's state.
🔄 The Role of the Detector in Quantum Systems
The paragraph discusses the role of the detector in quantum systems, noting that while it's treated separately from the system for simplicity, it too must obey quantum mechanical laws. It touches on the need to eventually consider the detector as a quantum system and the combined system as an interplay between two quantum systems. The paragraph also addresses the question of whether the detector stores memory and the nature of the state of a quantum system.
📐 Mathematics of Quantum State Spaces
This paragraph introduces the mathematical framework required to understand quantum state spaces, focusing on vector spaces. It distinguishes between the abstract concept of a vector space and the concrete idea of a vector as an arrow in space. The paragraph explains that vector spaces can consist of various mathematical objects, not just spatial vectors, and outlines the basic operations that can be performed on vectors within a vector space.
🔍 Complex Vector Spaces and Inner Products
The paragraph delves into complex vector spaces, explaining the properties and operations that define them, including addition and multiplication by complex numbers. It introduces the concept of the dual vector space and its relationship to the original vector space through complex conjugation. The paragraph also discusses the inner product of two vectors, highlighting its properties and how it relates to the concept of orthogonality in vector spaces.
🌟 Dimensionality and Orthogonality in Vector Spaces
This paragraph discusses the definition of dimensionality in vector spaces, relating it to the maximum number of mutually orthogonal vectors that can be found within the space. It provides examples of orthogonal vectors and explains that the number of components in a vector corresponds to the dimensionality of the space. The paragraph also touches on the concept of the zero vector and the closure requirement in vector spaces.
🔬 Quantum Mechanics and Vector Spaces
The final paragraph connects the abstract mathematics of vector spaces to the space of states in quantum mechanics. It emphasizes that the space of states for simple qubits is a two-dimensional vector space, contrasting with the idea of states as points in a set. The paragraph sets the stage for future discussions on how the mathematics of vector spaces can be used to represent the unusual logic of qubits and the properties of quantum measurements.
🤔 Final Questions and Conclusion
The paragraph concludes the discussion by addressing questions about the multiplication operation in vector spaces and the representation of inner products. It confirms that outer products of two vectors result in a matrix and that the postulates apply to a vector space of functions as well. The paragraph also acknowledges the random and uncorrelated nature of quantum measurements and the fundamental difference between classical and quantum mechanics regarding measurement disturbance.
Mindmap
Keywords
💡Classical Mechanics
💡State of a System
💡Qubit
💡Superposition
💡Quantum Measurement
💡Wave Function Collapse
💡Vector Space
💡Complex Numbers
💡Inner Product
💡Orthogonality
💡Quantum Entanglement
Highlights
Classical mechanics is based on concepts that are intuitive and drawn from everyday experiences, making it easier to visualize compared to quantum mechanics.
The French contribution to classical mechanics introduced mathematical elegance through concepts like Lagrangians and Poisson brackets, which are crucial for understanding the subject.
A system in classical mechanics is a closed, isolated entity whose state and evolution can be predicted deterministically.
The state of a system is a fundamental concept in classical mechanics, describing the collection of different states the system can have.
Equations of motion in classical mechanics are used to update the state of a system at any given time, allowing for predictions about its future behavior.
Quantum mechanics deals with abstract concepts that are beyond our ability to visualize, requiring the use of mathematics to describe phenomena.
The inability to visualize high-dimensional spaces or fast-moving particles in quantum mechanics necessitates an abstract approach to understanding these concepts.
Quantum mechanics introduces the concept of a qubit, which is a system with two states, analogous to a coin's heads or tails, but with a richer mathematical structure.
The state of a qubit can be represented by a vector in a two-dimensional space, with the directionality indicating the state of the system.
Measurement in quantum mechanics is not just about determining the state of a system but also about preparing the system in a particular state.
The act of measuring a quantum system like a qubit can disturb the system, leading to a new state, which is a fundamental difference from classical mechanics.
The logic of quantum mechanics is different from classical logic, with quantum states not being described by sets but by vector spaces.
The space of states in quantum mechanics is a vector space, which is a collection of mathematical objects that can be added and multiplied by complex numbers.
The dual vector space is a separate space whose elements correspond one-to-one with the original vector space, consisting of complex conjugate vectors.
The inner product of two vectors in a complex vector space is defined as the product of a vector and the dual of another vector, yielding a real number.
Orthogonality in complex vector spaces is defined by a zero inner product, and the maximal number of orthogonal vectors equals the dimensionality of the space.
The length of a complex vector is the square root of the inner product of the vector with itself, which is always real and positive.
Quantum mechanics involves probabilities and statistics, where the outcomes of measurements are not deterministic but follow a probability distribution.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: