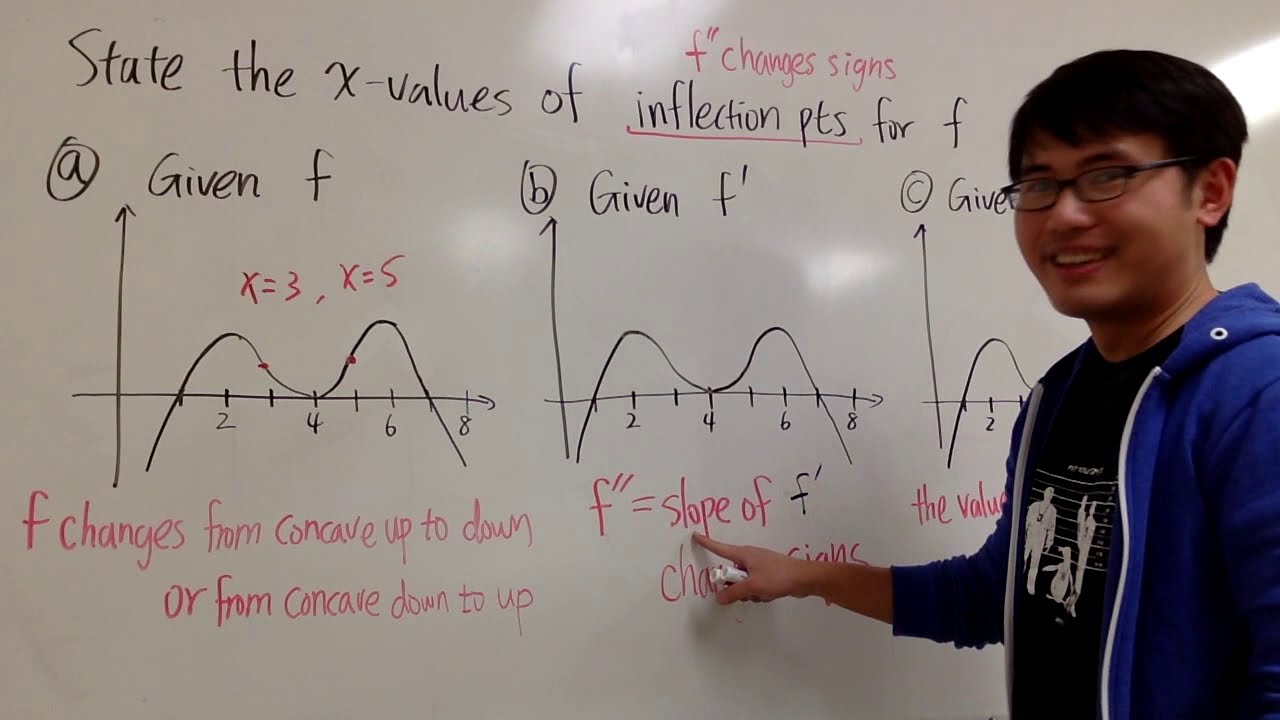
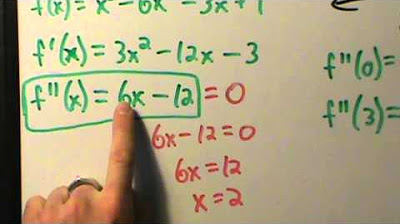Finding Concavity and Inflection Points

Professor Monte
3 Apr 202103:32
EducationalLearning
32 Likes 10 Comments

TLDRThe video script provides a detailed explanation on how to find concavity and inflection points of a function using the second derivative. The process begins by finding the first derivative of the given function, which is 3x^2 - 6x - 24. The second derivative is then calculated as 6x - 6. To locate the points of concavity and inflection, the second derivative is set to zero and solved, yielding a critical value of x = 1. The function's concavity is tested by evaluating the second derivative at points on either side of this critical value. The function is found to be concave down from negative infinity to 1 and concave up from 1 to infinity. The point where the concavity changes, x = 1, is identified as the inflection point. The corresponding y-value is calculated by substituting x = 1 into the original function, resulting in the inflection point being at (1, -21). The video concludes by emphasizing the importance of the second derivative in determining concavity and inflection points, and encourages viewers to subscribe for more informative content.

Takeaways
  • 📚 To find concavity and inflection points, start by taking the second derivative of the function.
  • 🔍 The first derivative of the given function is (3x^2 - 6x - 24), and the second derivative is (6x - 6).
  • ✍️ Set the second derivative equal to zero to find critical values for concavity and inflection points: (6x - 6 = 0).
  • 🔑 Solve the second derivative equation to find the critical value (x = 1).
  • 📈 Use a sign chart to test intervals around the critical value to determine the concavity of the function.
  • 📉 Test a point in each interval (e.g., (x = 0) and (x = 2)) by plugging it into the second derivative to check its sign.
  • 📶 A negative second derivative indicates the function is concave down, while a positive second derivative indicates it is concave up.
  • 🔄 At (x = 1), the concavity changes, which is the inflection point.
  • 📍 The inflection point is at (x = 1, y = -21), found by substituting (x = 1) into the original function.
  • 📝 The function is concave up from (x = 1) to infinity and concave down from negative infinity to (x = 1).
  • ⚠️ If there are more than one critical value, check the intervals between them to determine the concavity.
  • 📺 Subscribe to the channel for more educational content on mathematical concepts.
Q & A

  • What is the concept of concavity in calculus?

    -Concavity in calculus refers to the curvature of a function. A function is said to be concave up on an interval if the graph of the function lies above or on its tangent lines on that interval, and concave down if the graph lies below or on its tangent lines.

  • How is the second derivative used to find concavity?

    -The second derivative is used to determine the concavity by analyzing its sign. If the second derivative is positive over an interval, the function is concave up, and if it's negative, the function is concave down.

  • What is an inflection point?

    -An inflection point is a point on the graph of a function where the concavity changes. It's where the function transitions from being concave up to concave down or vice versa.

  • How do you find the inflection point mathematically?

    -To find an inflection point, you first find the second derivative of the function and set it equal to zero. Then you solve for x to find critical values. You test the intervals around these critical values by plugging in numbers from each interval into the second derivative to see where the concavity changes.

  • In the provided transcript, what is the first derivative of the function?

    -The first derivative of the function in the transcript is 3x^2 - 6x - 24.

  • What is the second derivative of the function in the transcript?

    -The second derivative of the function in the transcript is 6x - 6.

  • How does the sign of the second derivative indicate the concavity of the function?

    -If the second derivative is positive, the function is concave up, and if it's negative, the function is concave down. The sign change indicates an inflection point.

  • What is the critical value found in the transcript for the second derivative?

    -The critical value found in the transcript for the second derivative is x = 1.

  • How does the sign chart help in determining the concavity?

    -A sign chart divides the number line into intervals based on the critical values of the second derivative. By testing points within each interval, you can determine the sign of the second derivative and thus the concavity over each interval.

  • In the transcript, what are the intervals of concavity for the function?

    -In the transcript, the function is concave down from negative infinity to 1 and concave up from 1 to infinity.

  • How is the y-value of the inflection point found?

    -The y-value of the inflection point is found by substituting the x-value of the inflection point (the critical value where the concavity changes) back into the original function.

  • What is the inflection point found in the transcript?

    -The inflection point found in the transcript is at (1, -21).

  • What is the importance of subscribing to the channel as mentioned in the transcript?

    -Subscribing to the channel helps support the content creator by increasing the visibility of their videos, which can lead to more comprehensive and frequent content production.

Outlines
00:00
📚 Finding Concavity and Inflection Points

This paragraph explains the concept of concavity and inflection points in calculus. It begins by stating that concavity is determined by the second derivative of a function. The first derivative of the given function, 3x^2 - 6x - 24, is calculated to find the second derivative, 6x - 6. To find points of concavity and inflection, the second derivative is set to zero and solved, yielding x = 1 as a critical value. A sign chart is used to test intervals around this critical value to determine the concavity. The function is found to be concave down from negative infinity to 1 and concave up from 1 to infinity. An inflection point, where concavity changes, is identified at x = 1, with the corresponding y-value found by substituting x = 1 into the original function, resulting in y = -21. The paragraph concludes with a summary of the method for finding areas of concavity and inflection points using the second derivative.

Mindmap
Keywords
💡Concavity
Concavity refers to the curvature of a function. In the context of the video, it is derived from the second derivative of a function. A function is said to be concave up when its second derivative is positive, indicating it curves upwards like a U-shape, and concave down when the second derivative is negative, curving downwards like an inverted U-shape. The video uses concavity to analyze the shape of the function described by the equation 3x^2 - 6x - 24.
💡Second Derivative
The second derivative is the derivative of the first derivative of a function. It provides information about the concavity and inflection points of the original function. In the video, the second derivative of the function 3x^2 - 6x - 24 is calculated as 6x - 6, which is then used to find the points of concavity and inflection.
💡Inflection Point
An inflection point is a point on a curve where the concavity changes. It is identified when the second derivative of a function is equal to zero and changes sign. In the video, the inflection point is found by setting the second derivative to zero and solving for x, which results in x = 1. This point is where the function changes from being concave down to concave up.
💡Critical Value
A critical value is a value of the variable that makes the derivative equal to zero or undefined. In the video, x = 1 is identified as a critical value for the function's concavity. It is the point where the second derivative equals zero, indicating a potential change in the function's concavity.
💡Sign of the Second Derivative
The sign of the second derivative indicates whether a function is concave up or down. A positive second derivative corresponds to a concave up function, while a negative second derivative corresponds to a concave down function. In the video, the signs of the second derivative at different intervals are tested to determine the concavity of the function.
💡Number Line
The number line is a straight line that represents all real numbers, extending infinitely in both directions. In the video, the number line is used to segment the domain of the function into intervals based on the critical value, allowing the presenter to test different regions for concavity by plugging in test values.
💡Test Values
Test values are specific numbers chosen to evaluate the behavior of a function within certain intervals. In the video, the presenter selects 0 and 2 as test values to determine the sign of the second derivative in the intervals defined by the critical value x = 1.
💡Function's Original Equation
The original equation of the function is the mathematical expression that defines the function. In the video, the original function is given as 3x^2 - 6x - 24. This equation is used to calculate the first and second derivatives and to find the inflection point by substituting the x-value back into it.
💡Intervals
Intervals are the segments of the domain of a function that are created by critical values. In the video, the critical value x = 1 divides the domain into two intervals: negative infinity to 1 and 1 to infinity. The concavity of the function is analyzed separately for each interval.
💡Substitute
Substitution is the mathematical process of replacing a variable in an equation with a specific value. In the video, substitution is used to find the y-value of the inflection point by plugging x = 1 back into the original function's equation, resulting in y = -21.
💡Chart of Signs
A chart of signs is a tool used to determine the sign of the derivative over different intervals of the domain. In the video, the presenter uses a chart of signs to visualize and analyze the concavity of the function by testing the sign of the second derivative in the intervals defined by the critical value.
Highlights

The concept of concavity is derived from the second derivative of a function.

To find areas of concavity and inflection points, take the first derivative of the given function: 3x^2 - 6x - 24.

The second derivative is found to be 6x - 6, which is then set to zero to find critical points.

Solving the second derivative equal to zero yields a critical value of x = 1.

A chart of signs is used to test intervals around the critical value to determine concavity.

The function is tested at x = 0 and x = 2 to check the sign of the second derivative.

A negative second derivative at x = 0 indicates the function is concave down in the interval (-∞, 1).

A positive second derivative at x = 2 indicates the function is concave up in the interval (1, ∞).

An inflection point occurs where the concavity changes, which is at x = 1 in this case.

The y-value of the inflection point is found by substituting x = 1 into the original function, resulting in y = -21.

The function is concave up from x = 1 to ∞ and concave down from -∞ to x = 1.

The only inflection point is at (1, -21), indicating a change in concavity.

The process involves setting the second derivative to zero and solving for x to find critical values.

If there's more than one critical value, it's necessary to check the intervals between them.

The second derivative is key for identifying concavity and inflection points.

The video provides a step-by-step guide on how to find concavity and inflection points using the second derivative.

The presenter encourages viewers to subscribe to the channel for more educational content.

The video concludes with an invitation for viewers to leave comments and suggestions for future video topics.

Transcripts

Browse More Related Video

Calculus I: Finding Intervals of Concavity and Inflection point

Points of inflection from the graphs of f, f' or f''

How to Find Inflection Points

Maxima , minima and point of inflection

Increasing/Decreasing, Concave Up/Down, Inflection Points

Calculus I - Concavity and Inflection Points - Example 1

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
ConcavityInflection PointsSecond DerivativeMathematical AnalysisCritical ValuesFunction BehaviorGraph SignificanceEducational ContentMath TutorialDerivative CalculationWebinar