Precalc Chapter 5 Review

SupernovaMath

5 Mar 201829:46

EducationalLearning

32 Likes 10 Comments

TLDRThis video script offers a comprehensive review for a chapter 5 trigonometry test, focusing on verifying trigonometric identities, solving trigonometric equations, and applying sum and difference formulas. It explains the process of manipulating equations to match one side with the other, using identities and Pythagorean identities effectively. The script also covers solving for angles in different quadrants using reference angles and hand tricks, and simplifies expressions using double and half-angle formulas. The video aims to prepare students by walking them through various problems and providing calculator tricks for quick solutions.

Takeaways

📝 The video is a test review for Chapter 5, focusing on trigonometric identities and equations.
🔍 Verifying trig identities involves manipulating the left side of an equation to match the right side without altering the latter.
📈 Trigonometric identities can be simplified using basic trig functions and identities, such as converting tangent to sine over cosine.
✅ The goal in identity verification is to achieve a single trigonometric function on one side of the equation, often using Pythagorean identities.
🔢 Difference of squares and factoring techniques are applied in verifying certain trigonometric identities.
📚 A formula sheet is referenced for trigonometric identities, aiding in substitution and simplification.
📉 Trigonometric equations are solved by isolating the trig function and applying algebraic techniques like square roots and considering the sign of the result based on quadrants.
🤞 The 'hand trick' is introduced to determine reference angles for sine and cosine in different quadrants.
🔄 Reciprocal trig functions like cotangent are converted to their original trigonometric function for equation solving.
🔍 Sum and difference formulas for trigonometric functions are applied by rewriting expressions as the sum or difference of two angles.
📐 Double and half-angle formulas are used to simplify expressions involving multiples or halves of an angle, with attention to the correct application of plus or minus signs based on the angle's quadrant.

Q & A

What is the primary goal when verifying trigonometric identities?
-The primary goal when verifying trigonometric identities is to manipulate the left side of the equation so that it equals the right side without altering the right side.
What is a common strategy for simplifying trigonometric expressions involving addition or subtraction?
-A common strategy is to find a common denominator, which allows you to combine separate fractions into a single fraction for easier simplification.
How can you use Pythagorean identities to simplify an expression involving sine and cosine squared?
-You can use the Pythagorean identity \( \sin^2(\theta) + \cos^2(\theta) = 1 \) to simplify expressions by substituting the sum of sine and cosine squared with 1.
What is the difference between solving trigonometric equations for a specific interval versus all solutions?
-Solving for a specific interval, such as 0 to 2π, provides a finite set of solutions within that range. For all solutions, you would typically add \( 2\pi n \) to account for the periodicity of the trigonometric functions.
How can you determine the angles for which the sine function equals a positive value?
-The sine function is positive in the first and second quadrants. You can determine the specific angles by using reference angles and considering the periodicity of the sine function.
What is the significance of the 'hand trick' in solving trigonometric equations?
-The 'hand trick' is a mnemonic device to quickly find the reference angle for a given trigonometric value, which can then be used to determine the actual angles in the different quadrants.
How do you approach solving a trigonometric equation when you have a reciprocal function like cotangent?
-You change the reciprocal function back to its original trigonometric function. For cotangent, you would change it to the tangent function and then proceed to solve the equation.
What is the process for simplifying expressions using sum and difference formulas for cosine?
-You rewrite the expression as a sum or difference of two angles, and then apply the appropriate sum or difference formula for cosine, which involves terms like \( \cos(U)\cos(V) \) and \( \sin(U)\sin(V) \) or their variants.
How can you find the double angle formulas for sine and cosine?
-For sine, the double angle formula is \( \sin(2\theta) = 2\sin(\theta)\cos(\theta) \). For cosine, it can be expressed as \( \cos^2(\theta) - \sin^2(\theta) \), \( 2\cos^2(\theta) - 1 \), or \( 1 - 2\sin^2(\theta) \).
What is the purpose of half-angle formulas in trigonometry?
-Half-angle formulas are used to find the sine, cosine, and tangent of half of a given angle, which can be useful in simplifying complex trigonometric expressions.

Outlines

00:00

📚 Chapter 5 Test Review: Trigonometric Identities

This paragraph introduces the video's focus on Chapter 5 test review, specifically on verifying trigonometric identities. The speaker explains the process of manipulating the left side of an equation to match the right side without altering the right side itself. They demonstrate how to use trigonometric identities and substitution methods, such as converting tangent to sine over cosine, to simplify expressions. The goal is to achieve a single trigonometric function on one side of the equation. Examples include transforming an expression to equal secant of theta and factoring a difference of squares to verify an identity. The speaker emphasizes the importance of using a common denominator when adding fractions and leveraging Pythagorean identities.

05:04

🔍 Trigonometric Equations and Angle Solutions

The speaker transitions to solving trigonometric equations, emphasizing the need to isolate the trigonometric function. They demonstrate how to solve for sine squared and use square roots to find angles, utilizing the hand trick for reference angles. The explanation covers how to find angles in all four quadrants and how to express solutions within the interval of 0 to 2π. The paragraph also touches on the reciprocal relationships between trigonometric functions like cotangent and tangent, and how to use the hand trick to determine the signs of these functions in different quadrants.

10:10

📐 Trigonometric Equations: Isolating Trigonometric Functions

This paragraph delves deeper into isolating trigonometric functions in equations, using cosine as an example. The speaker shows how to manipulate equations to isolate cosine, then use the hand trick to find corresponding angles in different quadrants. They also discuss how to solve equations for all solutions by adding 2πn to the solutions found within the 0 to 2π interval. The explanation includes how to handle equations with sine and cosine, using reference angles and the hand trick to find all possible angles.

15:14

📘 Sum and Difference Formulas in Trigonometry

The speaker introduces sum and difference formulas for trigonometric functions, demonstrating how to rewrite expressions involving the sum or difference of angles. They show how to use formulas for cosine and sine of the sum or difference of two angles, applying them to specific examples. The explanation includes converting angles to degrees or radians as needed and using calculator tricks to simplify calculations. The paragraph also covers how to handle negative angles and how to simplify expressions using trigonometric identities.

20:15

🔢 Double and Half Angle Formulas Application

This paragraph focuses on double and half angle formulas, starting with a typo correction for a double angle problem. The speaker uses a triangle to illustrate how to apply these formulas, calculating cosine and sine for double angles. They demonstrate how to use the formulas for sine and cosine of double angles, as well as tangent, by substituting known values and simplifying the expressions. The explanation also covers half angle formulas, showing how to find the sine and tangent of half an angle using square roots and trigonometric identities.

25:15

📌 Half Angle Formulas and Tangent Calculations

The final paragraph covers half angle formulas in more detail, demonstrating how to find the sine and tangent of half an angle. The speaker shows how to determine the correct sign for the square root in the half angle formula based on the quadrant of the original angle. They also calculate the tangent of half an angle, using the formula and simplifying the expression. The explanation includes converting angles to the appropriate mode on a calculator and rationalizing denominators to obtain final answers.

Mindmap

Keywords

💡Trigonometric Identities

Trigonometric identities are equations that hold true for all values of the variable involved, often involving trigonometric functions like sine, cosine, and tangent. In the video, the main theme revolves around verifying these identities by manipulating one side of the equation to match the other, using the provided formula sheet. An example from the script is the transformation of tangent to sine over cosine and the use of Pythagorean identities to simplify expressions.

💡Pythagorean Identities

Pythagorean identities are specific trigonometric identities that relate the squares of sine and cosine functions to 1, such as \(\sin^2(\theta) + \cos^2(\theta) = 1\). The video explains how these identities are fundamental in simplifying expressions and verifying other trigonometric identities, as demonstrated when the instructor combines sine squared and cosine squared over a common denominator to equal secant theta.

💡Difference of Squares

The difference of squares is a mathematical concept where an expression of the form \(a^2 - b^2\) can be factored into \((a - b)(a + b)\). In the context of the video, the instructor applies this concept to simplify expressions involving trigonometric functions raised to the fourth power, as seen when sine to the fourth is factored into sine squared theta minus cosine squared theta.

💡Common Denominator

A common denominator is a single denominator that can be used for multiple fractions, allowing for the addition or subtraction of these fractions. The script mentions finding a common denominator when dealing with trigonometric expressions that need to be combined, such as multiplying fractions by \(\cos(\theta)/\cos(\theta)\) to combine terms into a single fraction.

💡Trigonometric Equations

Trigonometric equations involve trigonometric functions set equal to an expression that can be solved for the variable, often an angle. The video script discusses solving these equations by isolating the trigonometric function and then using methods like square roots and the hand trick to find the angle solutions within a given interval.

💡Sum and Difference Formulas

Sum and difference formulas are used to find the value of trigonometric functions when the argument is the sum or difference of two angles. The script refers to these formulas when simplifying expressions like \(\cos(135^\circ)\) by breaking it down into \(\cos(135^\circ - 60^\circ)\) and applying the formula for cosine of a difference of angles.

💡Double Angle Formulas

Double angle formulas are used to express the trigonometric functions of twice an angle in terms of the trigonometric functions of the original angle. The video script uses these formulas to find the values of \(\sin(2\theta)\), \(\cos(2\theta)\), and \(\tan(2\theta)\) by applying the appropriate formulas to the given angle, using the values of sine and cosine from a triangle with known sides.

💡Half Angle Formulas

Half angle formulas are used to find the value of a trigonometric function when the argument is half of another angle. In the script, the instructor uses the half angle formula for sine to find the value of \(\sin(75^\circ)\) by considering it as half of \(150^\circ\) and applying the formula \(\sin(\theta/2) = \pm\sqrt{\frac{1 - \cos(\theta)}{2}}\).

💡Hand Trick

The hand trick is a mnemonic device used to remember the values of sine, cosine, and tangent for common angles in a right triangle. The video script refers to this trick multiple times to find the reference angles for sine and tangent when solving trigonometric equations, such as placing the hand in a certain position to represent the angle \(\pi/3\) radians or \(60^\circ\).

💡Radian Mode

Radian mode is a setting on a calculator that allows for calculations to be performed using radian measures instead of degrees. The script mentions switching to radian mode when using a calculator to find the values of trigonometric functions for angles given in radians, such as when calculating \(\cos(\pi/6)\).

Highlights

The video provides a comprehensive review for a chapter 5 test focusing on trigonometric identities and equations.

The process of verifying trigonometric identities involves manipulating the left side of an equation to match the right side without altering the right side.

Trigonometric identities can be simplified using the formula sheet provided, such as changing tangent to sine over cosine.

The video demonstrates combining sine and cosine terms into a single fraction by finding a common denominator.

Pythagorean identities, such as sine squared plus cosine squared equals one, are used to simplify expressions.

The concept of difference of squares is introduced for simplifying expressions raised to the fourth power.

The video explains how to change cosecant to 1 over sine and combine fractions to simplify trigonometric expressions.

A step-by-step approach to solving trigonometric equations by isolating the trigonometric function is presented.

The use of the hand trick for determining angles in different quadrants based on the signs of trigonometric functions is discussed.

The video covers solving for angles within a specific interval and how to adjust for all solutions by adding 2πn.

The process of changing reciprocal trigonometric functions to their original form, such as cotangent to tangent, is explained.

The video introduces sum and difference formulas for cosine and how to use them to simplify expressions.

A calculator trick for quickly finding the values of cosine and sine for specific angles is shared.

Double angle formulas are demonstrated with examples, showing how to find the sine and cosine of double an angle.

Half angle formulas are introduced, and the video shows how to find the sine and tangent of half an angle.

The importance of using the correct mode on a calculator (degrees or radians) when working with trigonometric functions is emphasized.

The video concludes with a summary of the problems covered in the test review, aiming to prepare viewers effectively for their test.

Transcripts

Browse More Related Video

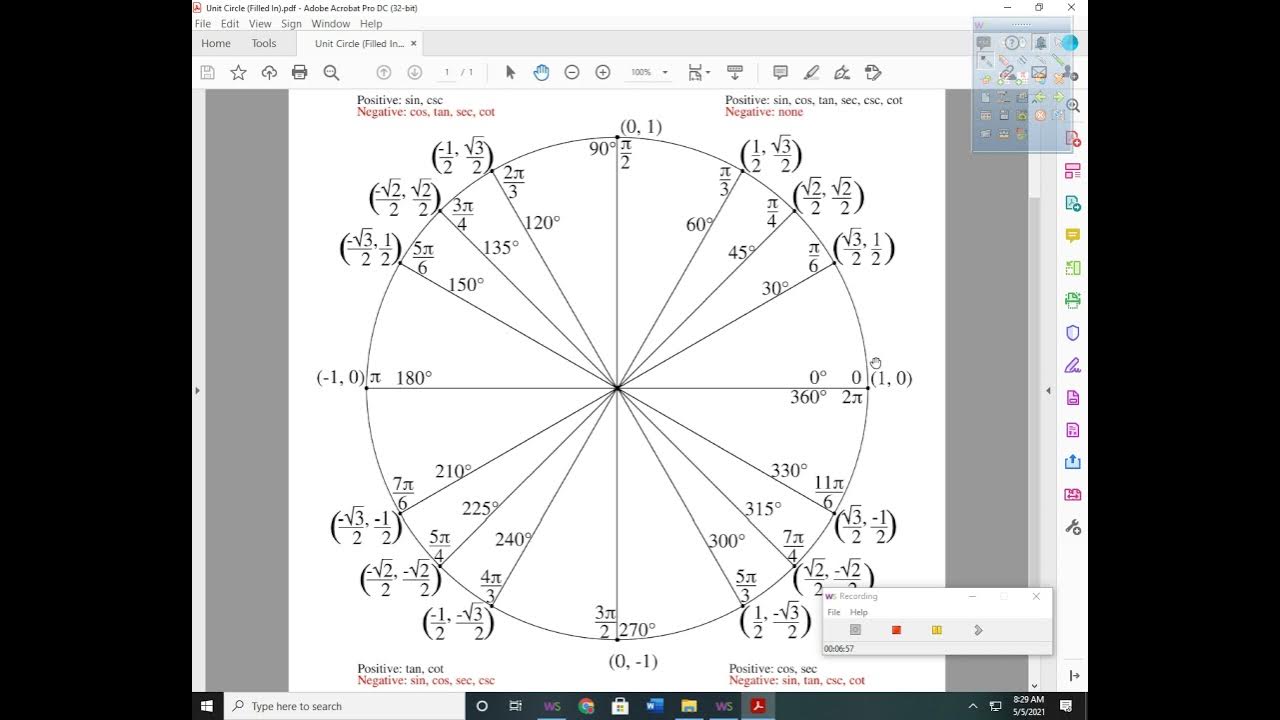
5.5 Multiple Angle and Product to Sum Formulas (Part 1)

Trig Identities

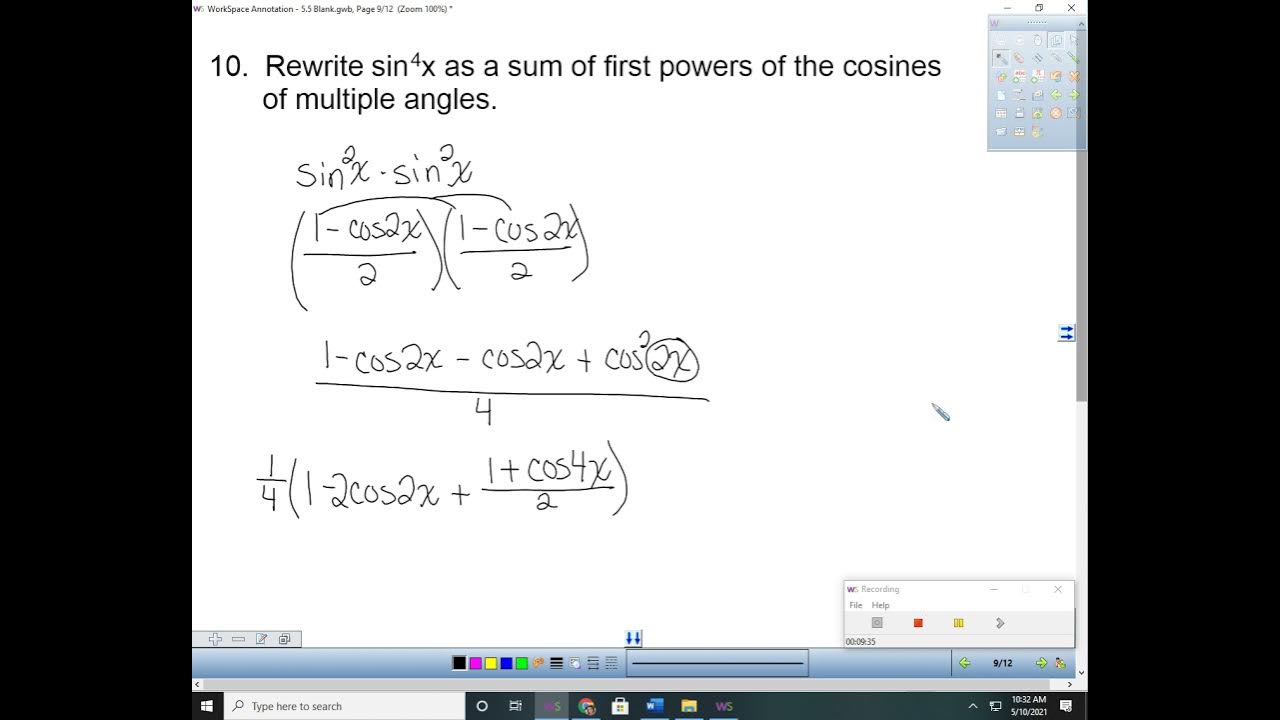
5.5 Multiple Angle and Product to Sum Formulas (Part 2)

How to Use the Double and Half Angle Formulas for Trigonometry (Precalculus - Trigonometry 28)

Verifying Trigonometric Identities With Double Angle Formulas

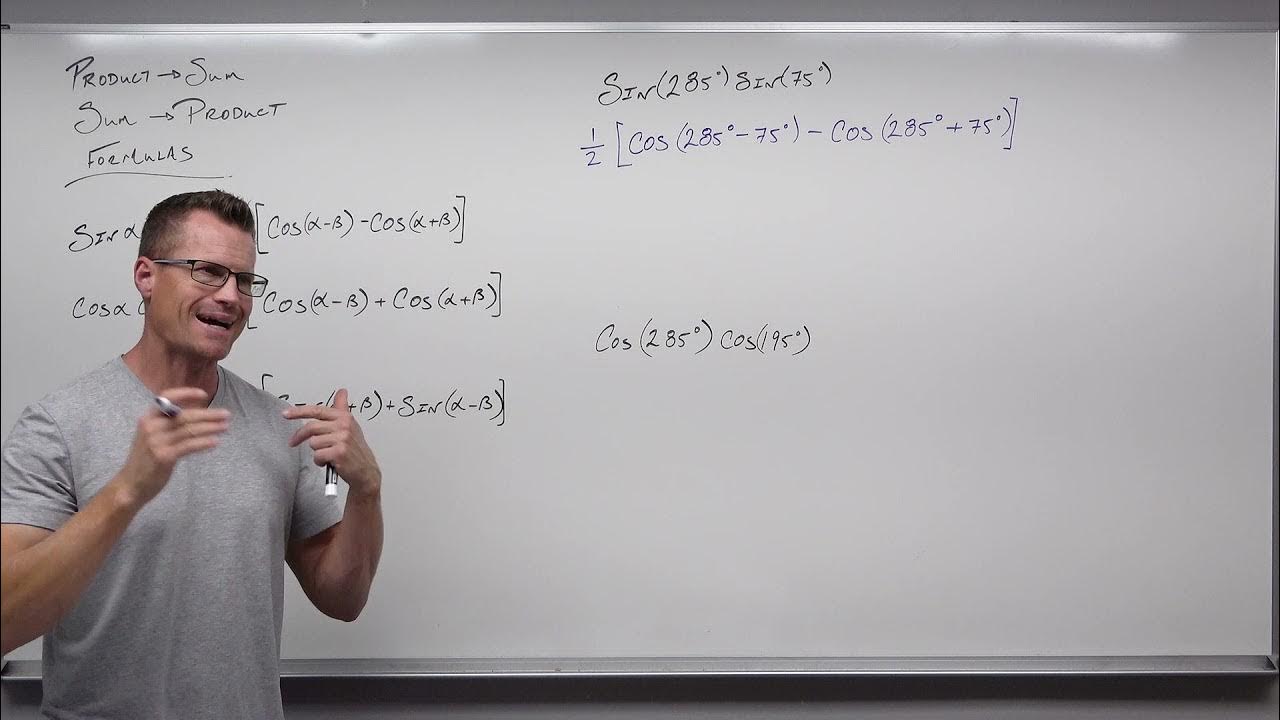
How to Use Product to Sum and Sum to Product Formulas in Trig (Precalculus - Trigonometry 29)

Related Tags

Trigonometry Test Review Identity Verification Trig Equations Double Angle Half Angle Pythagorean Identities Calculator Tricks Reference Angles Trig Functions