All of GRAVITATIONAL & ELECTRIC FIELDS in 12 mins - A-level Physics

Science Shorts
29 Oct 202312:47
EducationalLearning
32 Likes 10 Comments

TLDRThis script delves into the principles of gravitational and electric fields, highlighting their similarities and differences. It explains how these fields affect objects based on their mass and charge, and introduces the relevant equations and constants, such as Newton's law of gravitation and Coulomb's law. The concept of potential energy and its relationship with field strength is explored, along with the implications for satellite motion and the conditions for weightlessness and escape velocity. The script also touches on the practical applications of electric fields, like in Milikan's oil drop experiment.

Takeaways
  • 🌐 Gravitational and electric fields have similar principles, but gravitational fields affect all objects while electric fields only affect charged objects.
  • πŸ“ˆ Gravitational field strength (G) is measured in Newtons per kilogram and indicates the force of gravity on a 1 kg mass on Earth, which is 9.81 N/kg.
  • πŸ“Š The strength of a gravitational field decreases with distance, following an inverse square relationship with respect to the distance from the center of the mass source.
  • 🌍 On a small scale, gravitational fields can be considered uniform, with field lines appearing parallel, unlike the radial field lines around a massive body like Earth.
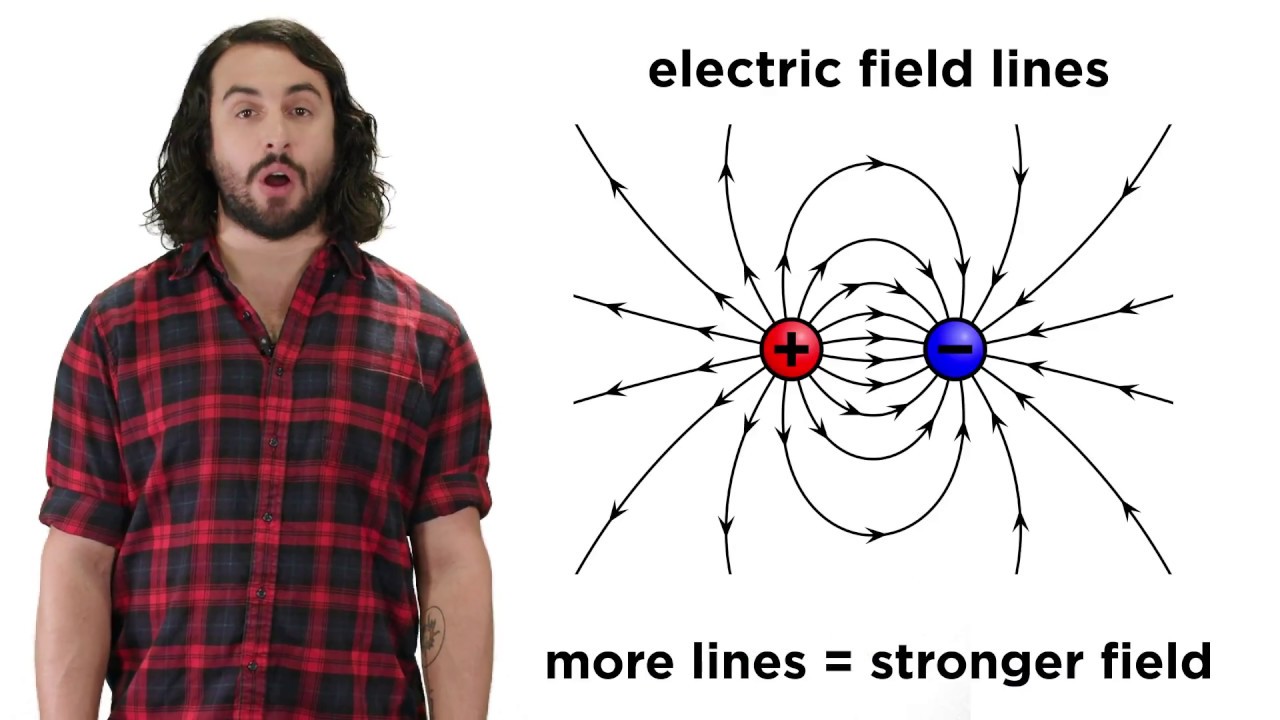
  • πŸ”‹ Electric fields can both attract and repel objects depending on their charge, with field lines indicating the direction of force on a positive charge.
  • 🌟 The universal gravitational constant (Big G) is approximately 6.67 * 10^-11 N(m/kg)^2, while the electric field constant (K) is 9 * 10^9 N(m^2/C^2).
  • πŸ“‰ The gravitational force inside a planet decreases linearly towards the center, where it becomes zero, due to the symmetry of forces in all directions.
  • πŸ”„ To compare field strengths on the surface of different planets, use the formula GMm/R^2 for gravity and kQq/R^2 for electric fields, where R is the distance from the center of the planet.
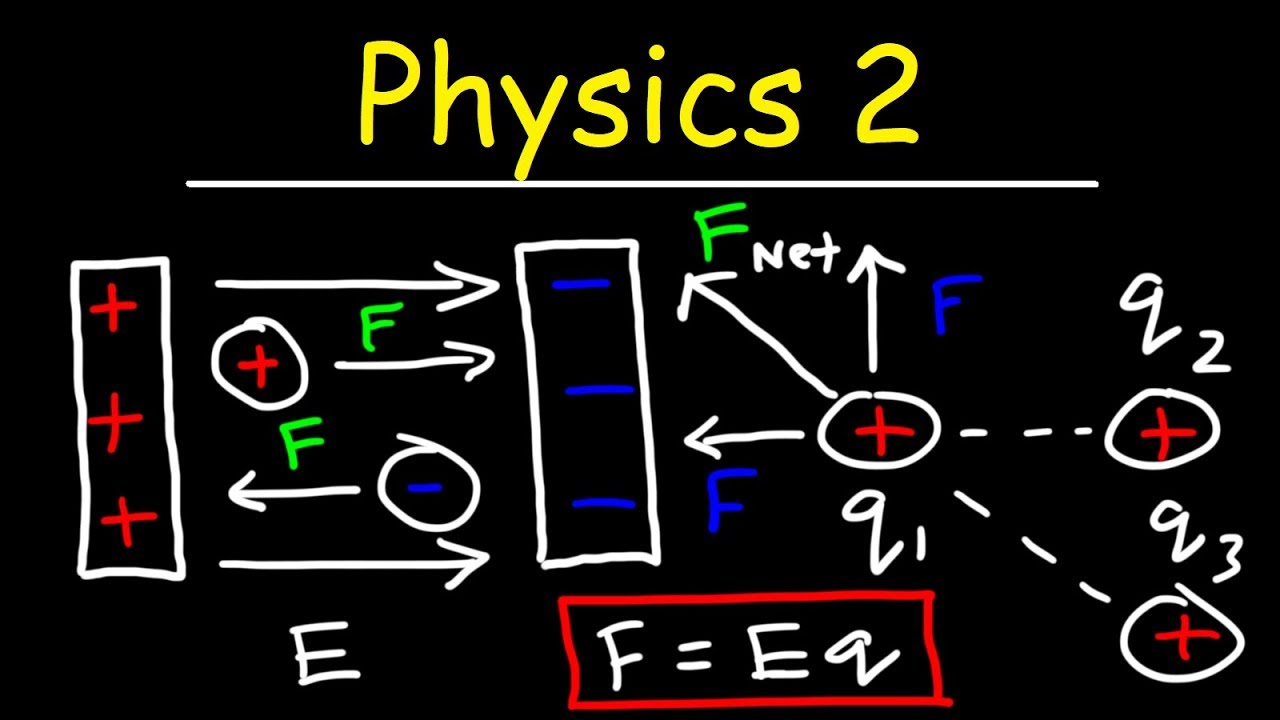
  • ⚑ The work done by a gravitational or electric field on an object is equal to the force times the distance moved, which can be used to calculate potential or electric potential energy.
  • πŸ›°οΈ Satellites in geosynchronous orbit have a period that matches the Earth's rotation (24 hours) and can only stay above the equator, while low polar orbits have shorter periods and cover different parts of the Earth.
  • πŸš€ The escape velocity from a planet's surface is the same for all objects, given by the equation V = √(2GM/R), where M is the mass of the planet and R is its radius.
Q & A

  • What is the difference between gravitational and electric fields in terms of how they affect objects?

    -Gravitational fields affect all objects, while electric fields only affect objects that have a charge. Gravitational fields are attractive and depend solely on mass, whereas electric fields can be either attractive or repulsive depending on the charges of the objects involved.

  • What is the unit of gravitational field strength G, and what does it represent?

    -The unit of gravitational field strength G is Newtons per kilogram (N/kg). It represents the force of gravity acting on each kilogram of mass an object has on Earth, which is 9.81 N/kg.

  • How does the gravitational field strength change with altitude?

    -The gravitational field strength decreases as you move higher from the Earth's surface. This is because the field strength is inversely proportional to the square of the distance from the center of the Earth.

  • What is the Universal Gravitational Constant, and what is its value?

    -The Universal Gravitational Constant, denoted by Big G, is a constant that appears in the equation for gravitational force. Its value is approximately 6.67 * 10^-11 N(m/kg)^2.

  • How do electric field lines behave around a positive charge, like a sphere from a Van de Graaff generator?

    -Electric field lines around a positive charge, such as a sphere from a Van de Graaff generator, point away from the charge. This is because a positive charge would be repelled if placed in the field.

  • What is the relationship between gravitational field strength and density inside a planet?

    -Inside a planet, gravitational field strength (G) is proportional to the radius (R). This is because density is proportional to mass over volume (m/R^3), so G is proportional to m/R^2, which simplifies to G ∝ 1/R when density is constant.

  • How can you find the point between two planets where there is no overall force or field?

    -The point between two planets where there is no overall force or field is found when the gravitational forces from each planet are equal (G1 = G2). This can be calculated using the formula GM1/R1^2 = GM2/R2^2, where R1 and R2 are the distances from the center of each planet to the point of interest.

  • What is the formula for gravitational potential energy, and how is it related to field strength?

    -The formula for gravitational potential energy (gpe) is gmm/R, where m is mass, g is the acceleration due to gravity, and R is the distance from the center of the mass source. This is related to field strength as the potential is proportional to the field strength (V ∝ 1/R) and can be thought of as the work done against the gravitational field to move an object to a certain point.

  • How does the electric potential change with distance in a uniform electric field?

    -In a uniform electric field, the electric potential (V) changes linearly with distance (R). The potential difference (Ξ”V) between two points is equal to the product of the field strength (E) and the distance (Ξ”R), so Ξ”V = E * Ξ”R.

  • What is the relationship between gravitational potential and electric potential at the surface of a planet?

    -At the surface of a planet, the gravitational potential (V) is given by minus GMm/R, where G is the gravitational constant, M is the mass of the planet, m is the mass of the object, and R is the distance from the center of the planet. For electric potential, it is given by KQ/R, where K is Coulomb's constant and Q is the charge creating the field. Unlike gravitational potential, electric potential can be zero between oppositely charged objects.

  • How can you determine the escape velocity from the surface of a planet?

    -The escape velocity (V) from the surface of a planet can be determined using the formula V = sqrt(2GM/R), where G is the gravitational constant, M is the mass of the planet, and R is the radius of the planet. This velocity represents the minimum speed needed for an object to break free from the planet's gravitational pull and reach infinity.

  • What is the significance of Kepler's Third Law in relation to satellite orbits?

    -Kepler's Third Law states that the square of the orbital period (T^2) of a satellite is proportional to the cube of the semi-major axis of its orbit (R^3). This law is significant as it allows us to predict the orbital periods of satellites and understand how changes in the distance from the planet (R) affect the time it takes for the satellite to complete one orbit.

Outlines
00:00
🌐 Understanding Gravitational and Electric Fields

This paragraph delves into the fundamentals of gravitational and electric fields, explaining how objects experience forces within these fields. It highlights the difference between the two, noting that gravitational fields affect all objects while electric fields only influence charged objects. The concept of field strength is introduced, with gravitational field strength having the unit of Newtons per kilogram, and its value on Earth being 9.81. The script also discusses how the strength of gravitational fields diminishes with altitude and how electric fields can either attract or repel objects based on their charge. The relationship between field strength, mass, and distance is explored, along with the constants used in equations to describe these fields. The paragraph concludes with an explanation of how to calculate the force exerted by these fields on an object.

05:01
πŸ“ˆ Potential Energy and Field Strength in Gravitational and Electric Fields

The second paragraph focuses on the concept of potential energy and field strength in both gravitational and electric fields. It introduces the idea of potential, which is the work required to move a unit mass from infinity to a specific point. The paragraph explains how potential is a scalar quantity and how it can be represented around a planet. It also discusses the relationship between potential and field strength, showing that the change in potential energy is equal to the mass or charge of an object multiplied by the change in potential. The concept of centripetal force is introduced in the context of satellite motion, and the relationship between speed, period, and radius is explored using Kepler's Law. The paragraph concludes with a discussion on geosynchronous orbits and the conditions required for a satellite to remain above the same point on Earth's surface.

10:03
πŸš€ Escape Velocity and the Dynamics of Charged Particles

The final paragraph discusses the concept of escape velocity, which is the minimum speed an object must achieve to break free from a planet's gravitational field. It explains that all objects, regardless of mass, have the same escape velocity at the surface of a planet. The paragraph then moves on to describe the behavior of charged particles in a uniform electric field, such as that created by parallel plates. It explains how the electric field accelerates charged particles and how the trajectory of these particles can be predicted. The concept of potential difference and its equivalence to electric potential is explored, along with the relationship between electric field strength and voltage. The paragraph concludes with a practical application of these concepts in the context of an experiment involving levitating objects in an electric field.

Mindmap
Keywords
πŸ’‘Gravitational Field
A gravitational field is a region in space where a mass experiences a force due to gravitational attraction. In the video, gravitational fields are discussed in terms of their effects on objects, distinguishing between uniform fields (where field lines are parallel and the strength is consistent, as within a small room on Earth) and radial fields (where the strength decreases with distance from the mass creating the field, such as around a planet). The video illustrates this by explaining how field lines and gravitational field strength vary with distance and location.
πŸ’‘Electric Field
An electric field is a region around a charged particle or object within which other charged particles experience a force, either attractive or repulsive depending on the charge type. The script compares electric fields to gravitational fields, noting that unlike gravitational fields which act on all masses, electric fields only interact with charged objects. Examples include the repulsion of a positive charge from a positively charged sphere or the attraction towards a negatively charged sphere.
πŸ’‘Field Lines
Field lines are imaginary lines used to represent the direction of the force exerted by a field (gravitational or electric) on objects. The video mentions that the density of these lines indicates the strength of the field: closer lines suggest a stronger field. This concept helps in visualizing how forces act in different types of fields, such as radial or uniform fields.
πŸ’‘Universal Gravitational Constant (Big G)
The Universal Gravitational Constant, denoted as Big G, is a key factor in the formula that calculates the force of attraction between two masses. It is a proportionality constant in Newton's law of gravitation. In the script, Big G is crucial for turning the proportional relationship between mass, distance, and gravitational force into a precise mathematical equation, facilitating calculations regarding gravitational interactions.
πŸ’‘Coulomb's Law
Coulomb's Law describes the force between two point charges. It states that the electric force between static charges is proportional to the product of the charges and inversely proportional to the square of the distance between them. This law is pivotal in understanding electric interactions, similar to how Newton's law of gravitation is used for gravitational interactions, as highlighted in the video.
πŸ’‘Equipotential
Equipotential lines or surfaces are locations within a field where the potential energy is constant. In the context of the video, equipotentials are discussed with reference to both gravitational and electric fields. They are particularly important for understanding energy conservation within these fields, showing how no work is done when moving along an equipotential line.
πŸ’‘Escape Velocity
Escape velocity is the minimum speed needed for an object to break free from the gravitational attraction of a planet or other body, without further propulsion. This concept is crucial in space travel dynamics, as discussed in the video, where it explains that escape velocity is derived from the energy balance between kinetic and potential energies at a planet's surface.
πŸ’‘Kepler's Law
Kepler's third law, mentioned in the video, relates the orbital period of a satellite to its distance from the center of the mass around which it orbits. It specifically states that the square of the orbital period is proportional to the cube of the radius of orbit. This law is fundamental in celestial mechanics, helping to predict satellite orbits and the dynamics of planetary systems.
πŸ’‘Potential Energy
Potential energy in the context of the video refers to the energy held by an object due to its position within a gravitational or electric field. The video explains gravitational potential energy (GPE) and electric potential energy in terms of work done against these forces, and how these energies change as objects move within these fields.
πŸ’‘Geostationary Orbit
A geostationary orbit is one in which a satellite has an orbital period that matches the Earth's rotation period and orbits in the direction of Earth's rotation. This type of orbit allows the satellite to appear stationary relative to a point on the Earth. The video uses this concept to discuss communication satellites, which require staying over a fixed point to provide consistent coverage.
Highlights

Gravitational and electric fields have similar working principles, with the key difference being that gravitational fields affect all objects, while electric fields only affect charged objects.

Gravitational field strength (G) is measured in Newtons per kilogram and indicates the force of gravity acting on each kilogram of mass. On Earth, this value is 9.81.

The gravitational field strength weakens as you move higher from the Earth's surface, which can be visualized by drawing field lines around the Earth.

In a uniform gravitational field, field lines are parallel, and the field strength is the same everywhere.

The universal gravitational constant (Big G) is approximately 6.67 * 10^-11 N(m/kg)^2, and it's used to calculate the force between two masses.

Electric field strength (E) has the unit Newtons per Coulomb (N/C) and is determined by the charge creating the field and the permittivity of free space (Epsilon 0).

For radial fields, gravitational field strength is proportional to the mass creating the field and inversely proportional to the square of the distance from its center.

Inside a planet, the gravitational field strength (G) is proportional to the radius (R), assuming constant density.

The gravitational force between two objects is given by Newton's law of gravitation, which is F = Big G * (m1 * m2) / R^2.

Coulomb's law for electric fields states that the force (F) between two charges (q1 and q2) is given by F = k * (q1 * q2) / R^2.

The work done by a gravitational or electric field on an object is equal to the force times the distance (W = F * d).

Gravitational potential (V) is defined as the work required to move a unit mass from infinity to a point in the field and is measured in Joules per kilogram (J/kg).

Electric potential is also a scalar quantity and is measured in Joules per Coulomb (J/C).

Equipotentials are lines of constant potential, and they are perpendicular to field lines, indicating that no work is done when moving along them.

The potential difference (Ξ”V) between two points in a field can be used to calculate the work done or energy transferred when moving an object between those points.

Centripetal force is required for circular motion, such as a satellite orbiting a planet, and is given by F = m * v^2 / R.

Kepler's third law relates the orbital period (T) of a satellite to the radius (R) of its orbit, with T^2 being proportional to R^3.

Geosynchronous satellites have an orbital period that matches the Earth's rotation, allowing them to stay above the same point on the Earth's surface.

The escape velocity from a planet's surface is determined by the formula V = √(2 * GM / R), where G is the gravitational constant, M is the planet's mass, and R is the planet's radius.

The distance of closest approach for a charged particle in an electric field can be found using the equation k * q * q / R = 0.5 * m * v^2, where q is the charge of the particle and R is the distance of closest approach.

Transcripts

Browse More Related Video

Gravitational Fields - A Level Physics

A Level Physics Revision: All of Gravitational Fields (in under 23 minutes)

Electric Charge and Electric Fields

Electric Charge and Light - Physics 101 / AP Physics 1 Review with Dianna Cowern

What is the Electric Field? How do Electric Forces Work?

Physics 2 - Basic Introduction

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics ConceptsGravitational FieldsElectric FieldsField StrengthPotential EnergyEscape VelocityCoulomb's LawNewton's LawSatellite MotionMagnetic Levitation