Gravitational Fields - A Level Physics
TLDRThis A-Level physics revision video delves into the concepts of gravitational and electric fields, emphasizing the idea of a field as a spatial phenomenon that exerts influence until a mass or charge interacts with it. It explains gravitational fields through Newton's law of universal gravitation, highlighting the inverse square relationship and the constant nature of gravitational force on Earth's surface. The video also explores the principles of centripetal force in orbiting bodies, the significance of geosynchronous satellites, and Kepler's laws of planetary motion. Finally, it touches on the concept of escape velocity, illustrating the minimum speed needed to break free from Earth's gravitational pull.
Takeaways
- 🌐 Fields are spatial constructs with values at every point, like a temperature field in a room.
- 📈 Gravitational fields cause mass to accelerate when placed within them, following an inverse square law.
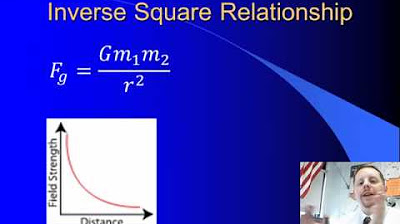
- 🔽 Newton's law of universal gravitation states that masses attract each other with a force proportional to their masses and inversely proportional to the square of the distance between them.
- 🌍 On Earth's surface, the gravitational force is constant for all objects, with the acceleration due to gravity being approximately 9.81 m/s^2.
- 🚀 To escape Earth's gravitational field, an object must reach a velocity of around 11 km/s, which is equivalent to 7 miles/s.
- 🌟 Kepler's laws describe the motion of planets in elliptical orbits around the Sun, with the planet sweeping out equal areas in equal times and the square of the orbital period being proportional to the cube of the semi-major axis of the orbit.
- 🪐 Geosynchronous satellites orbit Earth at a height of approximately 22,000 miles above the surface, completing an orbit in exactly 24 hours to remain stationary relative to the Earth.
- 🔄 The centripetal force required to keep an object in orbit is provided by the gravitational force between the object and the central body it is orbiting.
- 🌐 Electric fields, like gravitational fields, exert forces on charges placed within them, causing acceleration.
- 🔧 Newton's second law (F=ma) relates the force experienced by an object to its mass and acceleration, which can be applied to understand gravitational effects on objects near Earth's surface.
- 🌌 The concept of potential energy is introduced to describe the energy an object possesses due to its position in a gravitational field, which can be converted into kinetic energy.
Q & A
What is meant by the term 'field' in the context of physics?
-In physics, a 'field' refers to a region of space where a physical quantity, such as temperature or gravitational force, has a value at every point. It represents a physical influence that can affect objects within its domain.
How does a temperature field interact with an object placed in it?
-A temperature field does not actively do anything until an object is placed within it. When an object, such as ice, is placed in the field, it interacts with the field, leading to a change in the object's state, such as melting, due to the temperature difference.
What is the gravitational field, and how does it act until an object is placed in it?
-The gravitational field is a field that exists around a mass, such as a planet, and exerts a gravitational force on any object placed within it. It remains dormant until a mass is introduced, at which point it causes the mass to accelerate towards the source of the field.
Who discovered the principle that all masses attract one another, and what is the formula for the force of attraction between two masses?
-Sir Isaac Newton discovered that all masses attract one another. The force of attraction between two masses is given by the formula: F = -G * (m1 * m2) / R^2, where F is the force, G is the gravitational constant, m1 and m2 are the masses, and R is the distance between the centers of the two masses.
What is the significance of the gravitational constant (G) in the formula for gravitational force?
-The gravitational constant (G) is crucial for the dimensional consistency of the formula. It ensures that the units of force (Newtons), mass (kilograms), and distance (meters) are balanced, with G having units of N(m/kg)^2, allowing the equation to be dimensionally correct.
What is the value of gravitational acceleration (g) on the surface of the Earth?
-The value of gravitational acceleration (g) on the surface of the Earth is approximately 9.81 m/s^2. This is the acceleration that an object experiences due to Earth's gravity when it is near the surface.
How is the gravitational force experienced on the surface of the Earth simplified?
-On the surface of the Earth, the gravitational force is simplified to F = mg, where m is the mass of the object and g is the acceleration due to gravity (approximately 9.81 m/s^2). This is derived from the formula F = -G * (M * m) / R^2, with R being the Earth's radius and M being the Earth's mass.
What is the concept of gravitational potential energy, and how is it calculated?
-Gravitational potential energy (EP) is the energy an object possesses due to its position in a gravitational field. It is calculated using the formula EP = -G * M * m / R, where G is the gravitational constant, M and m are the masses of the two objects, and R is the distance between their centers.
What is the significance of the geosynchronous orbit for satellites?
-A geosynchronous orbit is significant because it allows a satellite to orbit the Earth with a period that matches the Earth's rotation period of 24 hours. This means the satellite remains stationary relative to a point on the Earth's surface, which is useful for applications like communication and weather monitoring.
What is the height above the Earth's surface required for a satellite to be in a geosynchronous orbit?
-For a satellite to be in a geosynchronous orbit, it must be approximately 35,900 kilometers (about 22,000 miles) above the Earth's surface, in addition to the Earth's radius of approximately 6,400 kilometers.
What are Kepler's three laws of planetary motion?
-Kepler's three laws of planetary motion are: 1) Planets move in elliptical orbits with the Sun at one focus; 2) A line joining a planet and the Sun sweeps out equal areas in equal times; and 3) The square of the orbital period of a planet is proportional to the cube of the semi-major axis of its orbit.
What is the escape velocity required to break free from Earth's gravitational pull?
-The escape velocity required to break free from Earth's gravitational pull is approximately 11 kilometers per second or about 25,000 miles per hour.
Outlines
🌌 Introduction to Gravitational Fields
This paragraph introduces the concept of gravitational fields, emphasizing their nature as a spatial phenomenon that exerts a force on objects placed within them. It explains that fields, such as temperature fields, have values at every point in space and interact with objects to produce effects. The gravitational field, in particular, is highlighted as a field that causes mass to accelerate when placed within it. The historical discovery by Newton that all masses attract each other is discussed, along with the formula for gravitational force, which is dependent on the masses of the objects and the distance between them. The concept of the gravitational constant and its role in the force equation is introduced, as well as the inverse square law, which describes the relationship between force and distance. The paragraph concludes with an explanation of how the force of gravity is directed and its relevance to larger bodies like Earth and the Sun.
📈 Gravitational Force and Earth's Gravity
This paragraph delves into the specifics of gravitational force as it relates to Earth. It explains that the gravitational force on Earth's surface is constant for all objects, with the only variable being their mass. The value of Earth's gravity, denoted as 'little g', is derived and its significance as an approximation of gravitational attraction near Earth's surface is discussed. The paragraph then introduces the concept of gravitational field lines and their direction relative to Earth. It also discusses the idea of potential energy and how work must be done to move an object against the gravitational field, resulting in potential energy. The concept of gravitational potential is also introduced, highlighting its relevance to the capability of moving a unit mass within the gravitational field.
🪐 Orbital Motion and Centripetal Force
This paragraph focuses on the motion of objects in orbit around Earth, such as spacecraft or the moon. It explains the gravitational force between two masses and how it is equal and opposite to the centripetal force required to keep an object in orbit. The concept of centripetal force is further elaborated by discussing the change in velocity and direction of an object moving in a circular path. The mathematical relationship between velocity, radius, and centripetal force is derived, leading to the equation that equates the gravitational force to the centripetal force. This relationship is used to derive the velocity of an orbiting body and the time it takes to complete one orbit. The concept of a geosynchronous orbit is introduced, explaining the conditions required for a satellite to appear stationary relative to Earth.
🚀 Geosynchronous Satellites and Orbital Periods
This paragraph discusses the specifics of geosynchronous satellites, which complete an orbit in exactly 24 hours, matching the Earth's rotation period. It explains the calculation of the required orbital radius for a satellite to maintain a geosynchronous orbit. The calculation involves the gravitational constant, Earth's mass, and the period of the orbit. The paragraph also covers the height of the satellite above Earth's surface, which is determined by subtracting Earth's radius from the orbital radius. The discussion then shifts to Kepler's laws of planetary motion, which describe the shape of orbits, the areas swept out by planets in equal times, and the relationship between a planet's orbital period and its distance from the Sun. These laws are shown to be closely related to the principles of gravitational force discussed earlier in the script.
🌠 Escape Velocity and Beyond
This paragraph explores the concept of escape velocity, which is the minimum speed needed for an object to break free from Earth's gravitational pull. It explains the relationship between kinetic energy and potential energy in the context of escaping Earth's gravity. The formula for calculating the escape velocity is derived, and the specific value for Earth is provided. The paragraph also discusses the practical implications of achieving escape velocity with a rocket, which can ascend more slowly due to its engine's continuous thrust. The concept is further illustrated with the hypothetical scenario of hitting a ball at escape velocity to send it into outer space. The paragraph concludes with a humorous comparison of the escape velocity to the serving speed of professional tennis players.
Mindmap
Keywords
💡Gravitational Field
💡Electric Field
💡Newton's Law of Universal Gravitation
💡Inverse Square Law
💡Gravitational Constant (G)
💡Acceleration Due to Gravity (g)
💡Geosynchronous Orbit
💡Kepler's Laws of Planetary Motion
💡Escape Velocity
💡Potential Energy
💡Centripetal Force
Highlights
Gravitational and electric fields are the focus of the A-Level physics revision series.
A field is a physical quantity that has a value at all points in space, such as temperature in a room.
Fields represent a capability to do something, but they only interact when an object is placed within them.
Newton discovered that all masses attract one another with a force described by the inverse square law.
The gravitational constant G is 6.67 × 10^-11 N(m/kg)^2, and it's essential for balancing the units in the equation.
On the surface of the Earth, the gravitational force is approximately 9.81 m/s^2, also known as little g.
Gravitational potential energy is given by the formula EP = -GMm/R, where M is the mass of the Earth and m is the mass of the object.
The gravitational potential is the capability of moving a unit mass against the gravitational field, given by V = EP/M.
Gravitational forces act between all masses, but they are only noticeable when one of the masses is large enough.
The velocity of an orbiting body is determined by the formula V = √(GM/R), where R is the distance from the center of the Earth.
The orbital period T is related to the radius R by the formula T^2 = (4π^2R^3)/GM.
A geosynchronous satellite orbits the Earth at a height of approximately 22,000 miles above the surface.
Kepler's laws of planetary motion describe that planets move in elliptical orbits and sweep out equal areas in equal times.
The escape velocity from Earth is approximately 11 kilometers per second or 25,000 miles per hour.
The concept of fields is central to understanding gravitational and electric interactions.
The gravitational field is a result of the mass of an object and affects other masses within its reach.
The force of gravity is a fundamental interaction that governs the motion of objects in the universe.
Understanding the principles of gravitational fields is crucial for space travel and satellite communications.
Transcripts
Browse More Related Video

A Level Physics Revision: All of Gravitational Fields (in under 23 minutes)

13.4a Orbital Mechanics | A2 Gravitational Fields | Cambridge A Level Physics

Gravitational Field Strength

AP Physics Workbook 3.M Gravitational Fields
AP Physics 1 Circular Motion and Gravitation Review
High School Physics - Newton's Law of Universal Gravitation
5.0 / 5 (0 votes)
Thanks for rating: