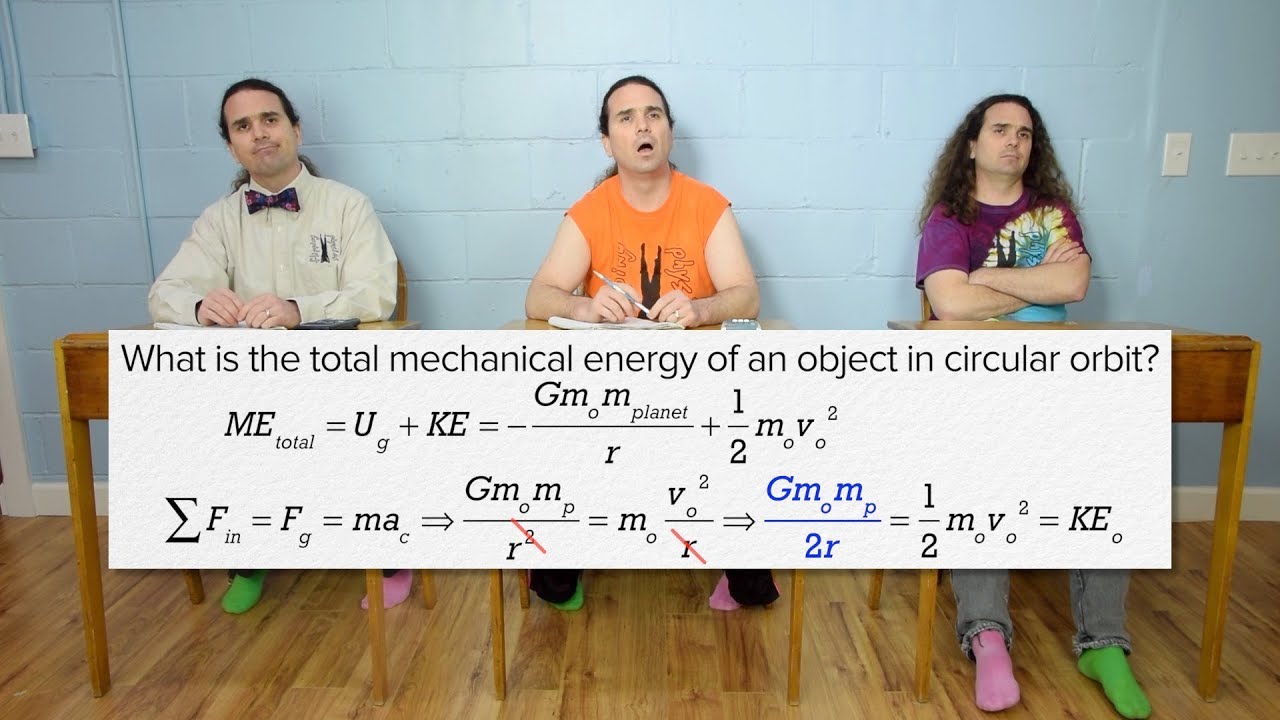A Level Physics Revision: All of Gravitational Fields (in under 23 minutes)

ZPhysics

28 Nov 202022:35

EducationalLearning

32 Likes 10 Comments

TLDRThis video from Zed Physics delves into the concept of gravitational fields, a key topic in OCR Physics. It explains how objects with mass create these fields, and how they can be represented with field lines. The video covers the formula for gravitational field strength, Newton's law of universal gravitation, and Kepler's laws of planetary motion. It also derives the formula for gravitational acceleration and explains how to calculate the height of a geostationary orbit using Kepler's third law. The concepts of gravitational potential energy, work done, and escape velocity are also discussed, providing a comprehensive review of the subject.

Takeaways

🌌 Gravitational fields are a result of objects having mass, causing an attractive force between any two massive objects.
📐 The strength of the gravitational field is represented by the density of gravitational field lines, with more lines indicating a stronger field.
📈 The formula for gravitational field strength is $g = rac{F}{m}$, measured in newtons per kilogram (N/kg) or meters per second squared (m/s²).
🌍 Gravitational forces are often modeled with spheres representing objects, assuming all mass is concentrated at the center.
🔄 Newton's law of universal gravitation states that the force of attraction between two masses is proportional to the product of their masses and inversely proportional to the square of the distance between them.
📊 Kepler's three laws of planetary motion describe the orbits of planets, including elliptical orbits with the sun at a focus, equal areas swept out in equal times, and the square of the orbital period being proportional to the cube of the orbital distance.
🚀 To calculate the height of a geostationary orbit, Kepler's third law can be applied, using the Earth's mass, radius, and the 24-hour orbital period.
🌐 Geostationary orbits have a fixed position relative to the Earth's surface, with an orbital period that matches the Earth's rotation period of 24 hours.
⚖️ Gravitational potential energy and gravitational potential are negative quantities that increase with distance, being zero at infinite distance.
🔢 The work done against gravity is represented by the area under the force-distance graph, and it is the energy required to move a unit mass from infinity to a point.
💥 Escape velocity is the minimum velocity required for an object to leave the gravitational field, calculated by setting gravitational potential energy equal to kinetic energy.

Q & A

What is the primary cause of gravitational fields?
-Gravitational fields are caused by objects having mass. Any two objects with mass will experience an attractive force due to their mass.
How are spheres represented in gravitational fields calculations?
-In A-level physics, spheres are often modeled as having all of their mass concentrated at a point, known as the center of mass, which simplifies calculations.
How are gravitational field lines depicted?
-Gravitational field lines are depicted as radial lines pointing towards the center of the mass that creates the field. The density of these lines represents the strength of the gravitational field.
What is the formula for gravitational field strength?
-The formula for gravitational field strength is g = F/m, where g is the gravitational field strength, F is the gravitational force, and m is the mass of the object experiencing the force.
What is Newton's law of universal gravitation?
-Newton's law of universal gravitation states that every point mass attracts every other point mass by a force acting along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them, expressed as F = G m1 m2/r^2, where F is the gravitational force, G is the gravitational constant, m1 and m2 are the masses, and r is the distance between the centers of the two masses.
What are Kepler's three laws of planetary motion?
-Kepler's first law states that the orbit of a planet is an ellipse with the sun at one of the foci. The second law states that a line segment joining a planet and the sun sweeps out equal areas in equal times. The third law states that the square of the orbital period of a planet is proportional to the cube of its orbital distance from the sun.
How can we calculate the height of a geostationary orbit using Kepler's third law?
-Using Kepler's third law, the height of a geostationary orbit can be calculated by rearranging the formula T^2 = 4pi^2/GM r^3 to solve for r, the distance from the center of the Earth to the satellite. The height above the Earth's surface is then found by subtracting the Earth's radius from this distance.
What are the defining characteristics of a geostationary orbit?
-A geostationary orbit has two main characteristics: its orbital period matches the Earth's rotation period of 24 hours, and it lies in the equatorial plane just above the Earth's equator. This means that the satellite remains fixed in the sky relative to an observer on Earth.
How is gravitational potential energy related to gravitational force?
-Gravitational potential energy is the energy a unit mass would have if it were moved from a reference point (usually infinity) to a specific point within a gravitational field. It is related to gravitational force as it represents the work done against gravity to move the mass to that point, and it is given by the formula U = -GMm/r, where U is the gravitational potential energy, G is the gravitational constant, M is the mass of the Earth, m is the mass of the object, and r is the distance from the center of the Earth to the object.
What is the concept of escape velocity?
-Escape velocity is the minimum velocity an object must have to escape the gravitational field of a celestial body without further propulsion. It is derived from setting the gravitational potential energy equal to the kinetic energy of the object and is calculated using the formula v = sqrt(2GM/r).
How does the gravitational potential change with distance from the source of the gravitational field?
-The gravitational potential decreases (becomes less negative) as the distance from the source of the gravitational field increases. It approaches zero at infinity, meaning that the potential is most negative at the location of the massive object and increases (gets less negative) with distance.

Outlines

00:00

🌌 Introduction to Gravitational Fields

This paragraph introduces the topic of gravitational fields, emphasizing their significance due to the mass of objects. It outlines the plan to follow the OCR Physics specification while also being applicable to other exam boards. The concept of modeling spheres as point masses is discussed, along with the representation of gravitational fields through field lines. The gravitational field strength is defined, relating it to the density of field lines and the formula for gravitational force and acceleration. The paragraph concludes with a note on the approximation of gravitational field strength near the Earth's surface.

05:00

📐 Kepler's Laws of Planetary Motion

This section delves into Kepler's three laws of planetary motion, explaining how they describe the orbits of planets around the sun. The first law outlines elliptical orbits with the sun at a focus, the second law discusses equal areas being swept out over equal times, indicating a variation in speed depending on proximity to the sun. The third law establishes a proportionality between the square of the orbital period and the cube of the orbital distance, supported by a derivation that connects this constant to gravitational force and centripetal force in circular motion.

10:03

🚀 Calculating Geostationary Orbits

The focus of this paragraph is on calculating the height of a geostationary orbit using Kepler's third law. It defines the characteristics of geostationary orbits, such as a 24-hour orbital period and equatorial positioning. The calculation involves rearranging the equation for orbital distance and incorporating the mass of the Earth and the gravitational constant. The height above the Earth's surface is determined by taking the cube root of a derived expression and subtracting the Earth's radius, resulting in a height of approximately 3.6 times 10 to the power of 7 meters.

15:05

⚙️ Gravitational Force, Potential Energy, and Work Done

This paragraph revisits the equations for gravitational force and gravitational potential energy, highlighting their negative values at infinite distance and their increase in negativity with distance. The concept of gravitational potential is introduced as the work done to bring a unit mass from infinity to a point. The work done is related to the area under a force-distance graph. The paragraph also touches on escape velocity, which is the minimum velocity required for an object to leave the gravitational field, derived by equating gravitational potential energy to kinetic energy and solving for the required velocity.

20:07

🎓 Revision and Conclusion

The final paragraph summarizes the key points covered in the video, reinforcing the understanding of gravitational fields, Newton's law of universal gravitation, and the concepts of gravitational potential energy and escape velocity. It also encourages viewers to subscribe and like the video for further educational content, rounding off the lesson with a call to action for continued learning.

Mindmap

Keywords

💡Gravitational Fields

Gravitational fields are the areas around massive objects where a force of attraction exists due to their mass. In the context of the video, it explains how any two objects with mass, such as spheres representing celestial bodies, will experience an attractive force towards each other. The strength of the gravitational field is depicted by the density of field lines, which are radial and point towards the center of the massive object, like a planet.

💡Newton's Law of Universal Gravitation

Newton's Law of Universal Gravitation states that every point mass attracts every other point mass by a force acting along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them. This law is fundamental in understanding gravitational fields and is used to derive the formula for gravitational force, which is F = -G * (m1 * m2) / r^2, where F is the gravitational force, G is the gravitational constant, m1 and m2 are the masses, and r is the distance between the centers of the two masses.

💡Gravitational Field Strength

Gravitational field strength is a measure of the intensity of the gravitational field. It is represented by the density of field lines, with twice as many field lines indicating a gravitational field twice as strong. Mathematically, it is defined as the gravitational force per unit mass (g = F/m) and is measured in newtons per kilogram (N/kg) or meters per second squared (m/s^2). Gravitational field strength is a key concept in understanding how objects interact within a gravitational field.

💡Kepler's Laws of Planetary Motion

Kepler's Laws of Planetary Motion are three scientific laws that describe the motion of planets around the sun. The first law states that the orbit of a planet is an ellipse with the sun at one of the foci. The second law, also known as the law of equal areas, states that a line segment joining a planet and the sun sweeps out equal areas during equal intervals of time. The third law establishes a relationship between the square of a planet's orbital period and the cube of its average distance from the sun, which can be expressed as T^2 ∝ r^3. These laws are fundamental in understanding the dynamics of celestial bodies in their orbits.

💡Geostationary Orbit

A geostationary orbit is a type of equatorial orbit in which a satellite remains at a fixed point relative to the Earth's surface, having an orbital period that matches the Earth's rotation period of 24 hours. This orbit is located above the equator and is at a specific altitude where the gravitational force acting on the satellite is balanced with the centripetal force required to maintain its circular orbit. Satellites in geostationary orbit are used for various applications, including weather observation, telecommunications, and satellite navigation.

💡Escape Velocity

Escape velocity is the minimum speed an object must reach to break free from the gravitational pull of a planet or other celestial body without further propulsion. It is the speed required to achieve an infinite orbit or to escape the gravitational field altogether. The formula for calculating escape velocity is v = √(2 * G * M / r), where v is the escape velocity, G is the gravitational constant, M is the mass of the celestial body, and r is the distance from the center of the body to the object trying to escape.

💡Gravitational Potential Energy

Gravitational potential energy is the energy an object possesses due to its position in a gravitational field. It is the work done against the gravitational force to move the object from a reference point (usually infinity) to its current position. The formula for gravitational potential energy is U = -G * M * m / r, where U is the potential energy, G is the gravitational constant, M is the mass of the Earth, m is the mass of the object, and r is the distance from the center of the Earth to the object. It is negative because it represents the work done to move the object against the gravitational force.

💡Work Done

Work done refers to the amount of energy transferred by a force acting over a distance. In the context of physics, it is calculated as the product of the force applied and the displacement in the direction of the force. The work done is often represented as the area under the force-displacement graph and is measured in joules. In the context of the video, work done is used to explain the concept of gravitational potential energy and how it relates to the force of gravity.

💡Centripetal Force

Centripetal force is the force that keeps an object moving in a circular path. It acts towards the center of the circle and is necessary to maintain circular motion. In the context of the video, centripetal force is used to explain the gravitational force acting on a planet in orbit around the sun, which is directed towards the center of rotation.

💡Orbital Period

The orbital period is the time taken for an object to complete one orbit around another object. In the context of the video, it is used to describe the time a planet takes to orbit the sun, which is related to the planet's distance from the sun through Kepler's third law. The orbital period is a crucial parameter in understanding the dynamics of celestial bodies and their motion in space.

Highlights

Gravitational fields are a result of objects having mass, causing an attractive force between any two massive objects.

In physics, spheres are often modeled as having all their mass concentrated at a point at the center, simplifying calculations in gravitational field equations.

Gravitational field lines are radial and point towards the center of the mass, with their density representing the strength of the gravitational field.

The formula for gravitational field strength is g = F/m, measured in newtons per kilogram (N/kg) or meters per second squared (m/s^2).

Newton's law of universal gravitation describes the attractive force between two masses, with the equation F = -Gm_1m_2/r^2, where G is the gravitational constant.

Gravitational acceleration is a measure of the gravitational field strength and is represented by the letter g.

Kepler's first law states that the orbit of a planet is an ellipse with the sun at one of the foci.

Kepler's second law, also known as the law of equal areas, states that a line segment joining the sun and a planet will sweep out equal areas in equal times.

Kepler's third law establishes a proportionality between the square of a planet's orbital period and the cube of its orbital distance, expressed as T^2 \propto r^3.

Geostationary orbits have an orbital period of 24 hours and are fixed in the sky relative to an observer on Earth, due to their alignment with the Earth's rotation.

The height of a geostationary orbit can be calculated using Kepler's third law, with the Earth's mass and radius as known constants.

Gravitational force is given by Newton's law of universal gravitation, F = -Gm_1m_2/r^2.

Gravitational potential energy is given by U = -Gm_1m_2/r, representing the energy per unit mass.

Both gravitational potential energy and gravitational potential are negative and increase with distance from the source of the gravitational field.

The work done to move an object against gravity is equal to the area under the force-distance graph, which represents the energy transfer.

Escape velocity is the minimum velocity required for an object to leave the gravitational field, calculated by setting gravitational potential energy equal to kinetic energy.

The escape velocity from Earth is approximately 11 kilometers per second, derived from the formula v = sqrt(2GM/r).

Transcripts

Browse More Related Video

Gravitational Fields - A Level Physics

AP Physics C: Universal Gravitation Review (Mechanics) - Also for JEE/NEET

AP Physics 1: Universal Gravitation Review

High School Physics - Gravitational Fields

All of GRAVITATIONAL & ELECTRIC FIELDS in 12 mins - A-level Physics

Gravitational Field Strength

Related Tags

GravitationalFields NewtonsLaw KeplersLaws PhysicsEducation SpaceOrbit GeostationaryOrbit EscapeVelocity PhysicsRevision ALevelPhysics ZedPhysics