Learn how to solve a related rate of loosing water from a cone
TLDRThe transcript describes a step-by-step process to solve a physics problem involving the rate of water drop in a container. The speaker explains how to define variables, establish relationships between height and radius based on given conditions, and differentiate the volume equation with respect to time to find the rate of change of height (dh/dt) when the water is three inches deep. The final calculation results in a negative value, indicating the water is dropping at a rate of approximately 0.503 inches per minute.
Takeaways
- 🧠 The problem involves calculating the rate at which water is dropping from a container with a specific geometry.
- 📝 The initial step involves identifying and defining the variables needed to solve the problem, such as height (h) and volume (V).
- 🔍 The script emphasizes the importance of understanding the relationship between the variables, particularly between height (h) and radius (r) of the container.
- 🌟 A key relationship established is that the height (h) is proportional to the radius (r), leading to the formula r = 3/8 * h.
- 📊 The volume of the water in the container is expressed as a function of height (h) using the formula V = (1/3 * π * (3h/8)^2 * h).
- 🚀 Differentiation is used to find the rate of change of height (dh/dt) with respect to time when the water level is at a certain depth.
- 🧮 The rate of water loss (dv/dt) is given as a constant negative value of -2 cubic inches per minute, representing the loss of volume.
- 🧱 The problem-solving process involves substituting the known values and solving for the unknown derivative (dh/dt) at a specific height (h = 3 inches).
- 📈 The final calculation yields a result of approximately -0.503 inches per minute, indicating the rate at which the height of the water is decreasing.
- 🔑 The script highlights the importance of breaking down complex problems into manageable parts and using proportional relationships to simplify calculations.
- 💡 The process demonstrates the application of mathematical concepts such as differentiation and proportional relationships in real-world scenarios.
Q & A
What is the main problem being discussed in the transcript?
-The main problem being discussed is determining the rate at which the water level (height) is dropping in a container, given that the water is losing volume at a constant rate and is at a certain depth.
What is the significance of steps three and four in the context of the problem?
-Steps three and four seem to be part of a method or procedure the speaker is using to solve the problem, but they are not directly helping to solve or find the solution in this specific case.
How is the variable 'h' defined in the problem?
-The variable 'h' represents the height of the water in the container, which is the key variable of interest when trying to determine how fast the water level is dropping.
What specific rate are they trying to find in the problem?
-They are trying to find the rate (dh/dt) at which the height of the water is changing with respect to time, at the instant the water is three inches deep.
Why is the volume loss (dv/dt) considered negative in this context?
-The volume loss (dv/dt) is considered negative because the water is being lost or removed from the container, as opposed to being added or gained.
What is the relationship established between the height 'h' and the radius 'r' of the container?
-The relationship established between the height 'h' and the radius 'r' is that r is equal to 3/8 times h, derived from the proportional relationship observed when the water is four inches deep and three inches across.
How does the speaker eliminate the variable 'r' from the calculations?
-The speaker eliminates the variable 'r' by finding a relationship between 'r' and 'h' and then replacing 'r' with its equivalent expression in terms of 'h', allowing the problem to be solved without directly dealing with 'r'.
What is the final expression derived for the volume of the water in terms of 'h'?
-The final expression derived for the volume of the water in terms of 'h' is (3/64)πh^3, which simplifies the problem to dealing with only one variable, 'h'.
What is the result of the calculation for the rate of change of height with respect to time (dh/dt) when the water is three inches deep?
-The result of the calculation for the rate of change of height with respect to time (dh/dt) when the water is three inches deep is approximately negative 0.503 inches per minute.
What is the significance of the negative sign in the final answer for dh/dt?
-The negative sign in the final answer for dh/dt signifies that the height of the water is decreasing over time, which is consistent with the fact that water is being removed from the container.
What is the second question that needs to be addressed after solving the first one?
-The second question that needs to be addressed is related to how fast the radius of the container is changing, which is a separate problem from the rate at which the water level is dropping.
Outlines
📚 Introduction to Problem Analysis
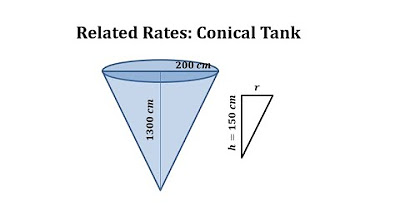
The speaker begins by setting up the problem, which involves a container losing water at a constant rate. The problem requires the calculation of the rate at which the water level is dropping at a specific depth. The speaker outlines the steps needed to solve the problem, emphasizing the importance of understanding the variables and the relationships between them. The initial focus is on identifying the variables and sketching a diagram to visualize the scenario. The speaker also mentions that the rate of water loss is negative since it's a decrease in volume.
📐 Establishing the Relationship between Radius and Height
The speaker corrects a mistake from the previous explanation, clarifying that the depth of water is four inches, not three. They then proceed to establish a relationship between the radius (r) and the height (h) of the water in the container. Using proportions, the speaker determines that the radius is equal to 3/8 times the height (r = 3/8h). This relationship is crucial as it allows the speaker to express the volume of the water in terms of height alone, which simplifies the problem by eliminating the need to account for the radius directly.
🔢 Derivation and Solution for Rate of Change
The speaker focuses on differentiating the volume equation with respect to time to find the rate of change of height (dh/dt) when the water is three inches deep. They use the relationship established in the previous paragraph to express the volume in terms of height and then differentiate it. The speaker sets up the equation with the given rate of volume loss (negative 2 cubic inches per minute) and solves for dh/dt when h is 3 inches. After performing the calculations, the speaker concludes that the rate of change of height with respect to time is approximately negative 0.503 inches per minute, indicating how quickly the water level is dropping at the specified depth.
Mindmap
Keywords
💡equation
💡variables
💡derivative
💡volume
💡rate
💡height
💡radius
💡proportions
💡differentiate
💡cubic inches
💡pi
Highlights
The speaker begins by analyzing a problem involving the rate of water dropping in a container.
The initial steps involve writing out the equation and identifying the variables needed to solve the problem.
The speaker notes the importance of understanding the question, which asks for the rate at which the water level is dropping when the water is three inches deep.
A key aspect of the problem is determining the rate of change of the water level (dh/dt) with respect to time.
The speaker emphasizes the need to find the relationship between the height (h) and the radius (r) of the container as the water level drops.
A proportion is used to establish that 1.5 is to h as r is to h, leading to the relationship r = 3/8 * h.
The volume of the water in the container is expressed in terms of h using the formula V = (1/3 * π * (3h/8)^2 * h).
The derivative of the volume with respect to time (dv/dt) is calculated, leading to an equation involving h and dh/dt.
The speaker clarifies that the problem is asking for the derivative of h with respect to time (dh/dt) when h is equal to three inches.
By substituting r with h in the volume equation, the speaker eliminates the need to deal with the unknown radius.
The final equation for the derivative of the volume with respect to time is simplified to involve only h.
The speaker calculates the value of dh/dt when the water is three inches deep, resulting in a final answer of negative 0.503 inches per minute.
The negative sign in the result indicates that the water level is decreasing.
The speaker acknowledges that there is a second question to be addressed after solving the first one.
Throughout the explanation, the speaker uses clear and methodical steps to guide the audience through the problem-solving process.
The problem-solving approach involves a combination of algebraic manipulation, geometric relationships, and calculus.
The speaker's method highlights the importance of understanding the context and constraints of the problem before attempting to solve it.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: