Related Rates Applicate: Leaking Conical Tank
TLDRThe video script presents a mathematical problem involving a conical tank where water is pumped in at a constant rate while simultaneously leaking out. The problem requires converting units from meters to centimeters and using the volume formula for a cone. The key is to equate the rate of change in volume due to the water being pumped in (dV/dt in) with the rate of change due to the water leaking out (dV/dt out). By setting up proportions based on similar right-triangles and differentiating the volume equation with respect to time, the script guides the viewer to solve for the unknown pumping rate. The solution process is methodically explained, leading to a final answer of approximately 48,352.9 cubic centimeters per minute as the rate of water being pumped into the tank.
Takeaways
- 💧 The problem involves a conical tank with water leaking out and being pumped in simultaneously.
- 📐 Water leaks at a rate of 8,200 cubic centimeters per minute, while the water level rises at 24 centimeters per minute.
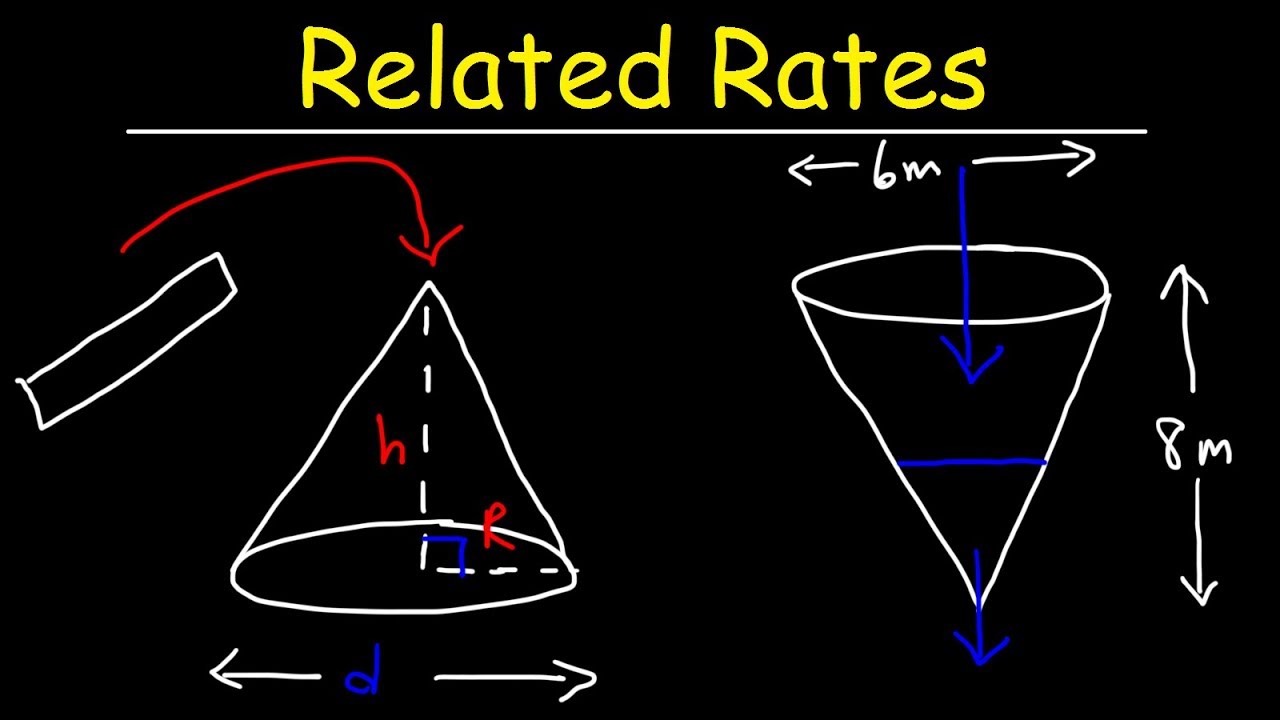
- 🌋 The conical tank has a height of 13 meters and a top diameter of 4 meters, which converts to 1,300 centimeters and 200 centimeters respectively.
- 📊 The volume of the conical tank is given by the formula v = 1/3 * π * r^2 * h, which is essential for calculating the rate of change in volume.
- 🔄 The rate of change in volume with respect to time (dV/dt) is the difference between the rate of water pumped in (dV/dt in) and the rate of water leaking out (dV/dt out).
- 📐 The relationship between the height (h) and radius (r) of the water level in the tank is established using similar right-triangles, resulting in r = 2/13 * h.
- 🔢 The volume formula is differentiated to find dV/dt, leading to the equation 13/6 * π * r^3 = 39/6 * π * r^2 * dr/dt.
- 🧠 The given water height of 1.5 meters (150 centimeters) and the rising rate of 24 centimeters per minute are used to find the radius and its rate of change at this height.
- 👷 The rate of change of the water height (dr/dt) is calculated as 48/13 centimeters per minute using the proportion of the radius to the height.
- 🔧 The final calculation for the rate at which water is being pumped into the tank (dV/dt in) results in approximately 48,352.9 cubic centimeters per minute.
- 📈 The problem-solving process involves unit conversion, application of geometric formulas, and the use of rates to solve a real-world scenario involving fluid dynamics.
Q & A
What is the rate at which water is leaking out of the conical tank?
-The rate at which water is leaking out of the conical tank is 8,200 cubic centimeters per minute.
How is the height of the conical tank given, and what is its equivalent in centimeters?
-The height of the conical tank is given as 13 meters, which is equivalent to 1,300 centimeters.
What is the diameter and radius of the conical tank, and how are they converted into centimeters?
-The diameter of the conical tank is four meters, which gives a radius of two meters. When converted into centimeters, the radius becomes 200 centimeters.
What is the rate at which the water level is rising in the tank?
-The water level in the tank is rising at a rate of 24 centimeters per minute.
What is the height of the water in the tank when we are trying to find the pumping rate?
-The height of the water in the tank when we are trying to find the pumping rate is 1.5 meters, which is equivalent to 150 centimeters.
How are similar right-triangles used to relate the radius and height of the water level in the tank?
-Similar right-triangles are used to form a proportion relating the radius (r) and height (h) of the water level. The proportion is r/200 = h/1300, which can be solved to find the relationship between r and h.
What is the volume formula for a conical tank and how is it expressed in terms of the radius?
-The volume formula for a conical tank is V = (1/3)πr^2h. By using the relationship derived from the similar triangles, h = (13/2)r, the formula can be expressed in terms of the radius alone as V = (13/6)πr^3.
How is the volume change with respect to time calculated for the water in the tank?
-The volume change with respect to time (dV/dt) is calculated by differentiating the volume formula with respect to time, resulting in dV/dt = (13/2)πr^2(dr/dt).
What is the relationship between the rate of change of the water height (dh/dt) and the rate of change of the radius (dr/dt)?
-The relationship between the rate of change of the water height (dh/dt) and the rate of change of the radius (dr/dt) is given by dr/dt = (2/13)dh/dt. Since dh/dt is 24 cm/min, dr/dt is (2/13) * 24 cm/min = 48/13 cm/min.
What is the final expression used to find the rate at which water is being pumped into the tank?
-The final expression used to find the rate at which water is being pumped into the tank is dV/dt (in) = -8,200 + (13/2)π(300/13)^2 * (48/13).
What is the approximate rate at which water is being pumped into the tank in cubic centimeters per minute?
-The approximate rate at which water is being pumped into the tank is 48,352.9 cubic centimeters per minute.
How does the problem demonstrate the use of geometry and algebra in solving real-world problems?
-This problem demonstrates the use of geometry to understand the relationship between the dimensions of a conical tank and the algebra to calculate the rates of water flow, showing how mathematical concepts can be applied to practical situations.
Outlines
📚 Introduction to the Conical Tank Problem
This paragraph introduces a mathematical problem involving an inverted conical tank where water is leaking out at a rate of 8,200 cubic centimeters per minute while being pumped in at a constant rate. The tank dimensions are given with a height of 13 meters and a top diameter of four meters. The challenge is to find the pumping rate when the water level is rising at 24 centimeters per minute with a water height of 1.5 meters. The paragraph emphasizes the need to convert units from meters to centimeters for consistency and introduces the volume formula for a cone (V = 1/3πr²h). It also sets the foundation for the problem-solving approach by discussing the relationship between the change in volume with respect to time (dV/dt) and the rates of water leaking (dV/dt out) and being pumped in (dV/dt in).
🔢 Solving the Conical Tank Problem
This paragraph delves into the solution of the conical tank problem by using the derived relationships from the first paragraph. It starts by establishing the proportional relationship between the radius (r) and height (h) of the water level in the tank, leading to the equation r = 2/13h. Using this, the paragraph proceeds to calculate the volume (V) in terms of r and then differentiates it with respect to time (t) to find dV/dt. The substitution of h with 13/2r in the volume formula results in a simplified form of dV/dt = 13/2πr²(dr/dt). With the known values of water height (150 cm), the rate of water level rise (24 cm/min), and the leaking rate (-8,200 cm³/min), the paragraph concludes by solving for the pumping rate (dV/dt in), which is approximately 48,352.9 cubic centimeters per minute.
Mindmap
Keywords
💡Water leakage
💡Conical tank
💡Pumping rate
💡Volume formula
💡Rate of change
💡Unit conversion
💡Right-triangles
💡Differentiation
💡Water level rise
💡Net change
💡Dimensions
Highlights
The problem involves a conical tank with water leaking and being pumped simultaneously.
The rate of water leakage is 8,200 cubic centimeters per minute.
Water is being pumped into the tank at a constant rate, with the water level rising at 24 centimeters per minute.
The conical tank has a height of 13 meters and a top diameter of four meters.
When the water height reaches 1.5 meters, the goal is to find the pump rate.
Unit conversion is necessary to solve the problem, changing meters to centimeters for consistency.
The volume formula for a cone, V = 1/3 * pi * r^2 * h, is used to calculate the volume of water in the tank.
The concept of similar right-triangles is utilized to form a proportion relating the radius and height of the water level.
The derived proportion is r = 2/13 * h, which can be rearranged to h = 13/2 * r.
Volume and its derivative with respect to time are used to find the rate of change in volume due to pumping and leaking.
The derivative of the volume equation with respect to time yields dV/dt = 13/2 * pi * r^2 * dr/dt.
The water height of 1.5 meters is used to find the corresponding radius of the water level.
The rate of change of the water level radius, dr/dt, is calculated using the given dh/dt and the proportion r = 2/13 * h.
The final equation to find the pump rate involves substituting the known values and solving for dV/dt in.
The pump rate is found to be approximately 48,352.9 cubic centimeters per minute.
The problem-solving approach combines geometry, algebra, and calculus to address a real-world scenario.
The solution process demonstrates the practical application of mathematical concepts in engineering and physics.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: