Physics 1 Formulas and Equations - Kinematics, Projectile Motion, Force, Work, Energy, Power, Moment

The Organic Chemistry Tutor

1 Oct 202342:22

EducationalLearning

32 Likes 10 Comments

TLDRThis video script offers a comprehensive review of essential physics formulas for first-year physics students. It covers topics such as kinematics, projectile motion, relative velocity, vectors, Newton's laws, forces, uniform circular motion, work, energy, power, springs, momentum, impulse, rotational motion, and gravitational force. The script is designed to aid students in understanding and applying these fundamental concepts, preparing them for exams and deepening their knowledge of physics.

Takeaways

📌 The formula for constant speed motion is D = VT, where D is displacement, V is velocity, and T is time.
📌 For constant acceleration motion, the displacement formula is D = (V_initial + V_final)/2 * T.
📌 The final velocity in constant acceleration is given by V_final = V_initial + Acceleration * T.
📌 In projectile motion, the only force acting is gravity, and the kinematic formulas for constant acceleration apply.
📌 The maximum height and range of a projectile can be calculated using V_initial, angle of projection, and gravitational acceleration.
📌 Relative velocity is the velocity of one object with respect to another and is calculated by subtracting the velocity of the second object from the first.
📌 Vector components can be calculated using trigonometric functions, with VY = V * sin(Theta) and VX = V * cos(Theta).
📌 Newton's laws of motion describe the relationship between force, mass, and acceleration, with F = m*a being the fundamental second law equation.
📌 Work done by a force is calculated as W = F*D, and power is the rate at which work is done, P = W/T.
📌 In uniform circular motion, centripetal force and acceleration are directed towards the center, with the formula for acceleration being a = V^2/R and for centripetal force being F = m*a.
📌 The work-energy theorem states that the net work done on an object is equal to the change in its kinetic energy, and for conservative forces, it's equal to the negative change in potential energy.

Q & A

What is the formula for displacement with constant speed?
-The formula for displacement with constant speed is D = V * t, where D is displacement, V is velocity, and t is time.
How is velocity different from speed?
-Velocity is displacement divided by time and it has both magnitude and direction, making it a vector quantity. Speed, on the other hand, is the magnitude of velocity and does not have a direction, making it a scalar quantity.
What is the formula for final velocity in the case of constant acceleration?
-The formula for final velocity with constant acceleration is V_final = V_initial + a * t, where V_final is the final velocity, V_initial is the initial velocity, a is the acceleration, and t is the time.
How can you calculate the displacement when dealing with constant acceleration?
-For constant acceleration, the displacement can be calculated using the formula D = V_average * t, where D is displacement, V_average is the average velocity (which is (V_initial + V_final) / 2), and t is the time.
What is the formula for projectile motion in terms of horizontal and vertical displacement?
-The formula for projectile motion is D = V_initial * t + 0.5 * a * t^2 for horizontal displacement, and y_final = y_initial + V_initial * t + 0.5 * a * t^2 for vertical displacement, where D is the horizontal displacement, y_final is the final vertical position, y_initial is the initial vertical position, V_initial is the initial velocity, a is the acceleration (due to gravity), and t is the time.
How do you calculate the maximum height reached by a projectile?
-The maximum height reached by a projectile can be calculated using the formula V_initial^2 * sin^2(Theta) / (2 * g), where V_initial is the initial velocity, Theta is the launch angle, and g is the acceleration due to gravity.
What is the relationship between linear velocity and angular velocity in rotational motion?
-In rotational motion, the relationship between linear velocity (V) and angular velocity (Omega) is given by V = Omega * R, where R is the radius of the rotation.
How is work calculated in physics?
-Work (W) is calculated as the product of the force (F) applied and the displacement (D) in the direction of the force, W = F * D. For work involving an angle, it is calculated as W = F * D * cos(theta), where theta is the angle between the force vector and the displacement vector.
What is the work-energy theorem?
-The work-energy theorem states that the net work done on an object is equal to the change in its kinetic energy. Mathematically, it is expressed as W_net = ΔKE, where W_net is the net work done on the object and ΔKE is the change in kinetic energy.
How is the force required to stretch a spring related to its spring constant and displacement?
-The force (F) required to stretch or compress a spring is given by F = -K * X, where K is the spring constant and X is the displacement from its natural length. The negative sign indicates that the force exerted by the spring is in the opposite direction of the applied force.
What is the formula for elastic potential energy stored in a spring?
-The elastic potential energy (PE) stored in a spring is given by PE = 0.5 * K * X^2, where K is the spring constant and X is the displacement from the spring's natural length.
How is power related to work and time in physics?
-Power (P) is defined as the rate at which work is done or energy is transferred. It is calculated as P = W / t, where W is work done and t is the time over which the work is performed.

Outlines

00:00

📚 Introduction to Common Physics Formulas

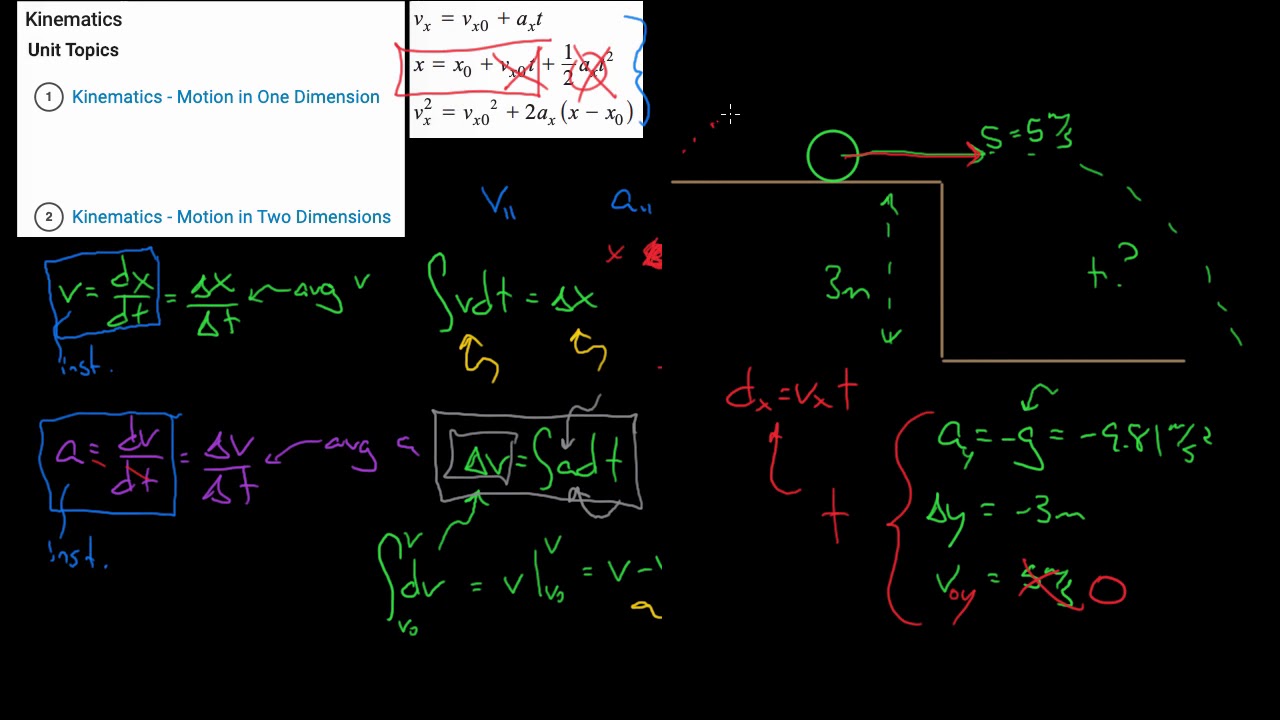
This paragraph introduces the video's focus on essential physics formulas, particularly those related to motion and kinematics. It emphasizes the importance of understanding these formulas for students currently studying physics or preparing for exams. The first formula discussed is for constant speed motion, where displacement (D) is equal to velocity (V) times time (T). The distinction between speed and velocity is clarified, with speed being a scalar quantity (always positive) and velocity being a vector (which can be positive or negative). The paragraph also covers formulas applicable to motion with constant acceleration, including final velocity (V_final) and displacement with examples and explanations.

05:02

🚀 Projectile Motion and Relative Velocity

The second paragraph delves into projectile motion, explaining how the previously discussed kinematic formulas apply to objects moving solely under the influence of gravity. It covers the conditions for projectile motion and introduces the concept of the trajectory, highlighting the highest point where vertical velocity is zero. Formulas for calculating maximum height, range, and time of flight for projectiles are provided, along with a brief introduction to relative velocity, emphasizing the main equations needed to solve problems involving it.

10:02

🔢 Vectors and Newton's Laws of Motion

This paragraph introduces the concept of vectors in physics, explaining how they can represent various physical quantities like velocity, acceleration, and force. It provides formulas for calculating the components of a vector based on its angle from the horizontal axis. Newton's laws of motion are then discussed, with explanations of how they relate to an object's state of motion and the forces acting upon it. The weight force and friction, including kinetic and static friction, are also defined with their respective formulas, emphasizing their importance in understanding force dynamics.

15:06

⭕ Uniform Circular Motion and Work-Energy Principles

The fourth paragraph focuses on uniform circular motion, defining centripetal acceleration and centripetal force, and providing formulas for calculating velocity and period. It connects these concepts to work and energy principles, discussing how work is done by a force and how it relates to the change in an object's kinetic energy. The work-energy theorem is explained, along with the concept of potential energy, particularly gravitational potential energy, and its relationship with work done by gravity.

20:07

🔄 Springs and Elastic Potential Energy

This paragraph discusses springs, starting with the concept of spring constant and the force required to stretch or compress a spring. It introduces the formula for elastic potential energy in a spring and explains how it relates to the spring's compression or extension. The paragraph also connects the concepts of work and energy to springs, explaining how work done on a spring is converted into stored energy and how the release of this energy can do work.

25:07

💡 Power, Momentum, and Impulse

The sixth paragraph introduces the concept of power, relating it to work and energy transfer rates. It provides the formula for power and explains its connection to force and velocity. The paragraph then moves on to discuss momentum and impulse, defining them and presenting the impulse-momentum theorem. It explains how changes in momentum relate to forces and how these concepts can be applied to calculate forces in various scenarios, such as rocket propulsion and water flow from a hose.

30:10

🌀 Rotational Motion and Angular Quantities

This paragraph explores rotational motion, starting with the relationship between angular displacement and linear displacement. It defines angular velocity and acceleration, and provides formulas relating them to linear quantities. The paragraph also covers rotational kinematics, including formulas for final angular velocity and angular displacement, and explains how they relate to linear kinematics. Inertia and rotational inertia are introduced, with formulas for different objects and scenarios, and the paragraph concludes with a discussion on torque, relating it to force and its rotational equivalent.

35:11

🌍 Gravitational Force and Simple Harmonic Motion

The final paragraph discusses gravitational force, explaining how it works between two masses and providing the formula for calculating it. It also covers gravitational acceleration and potential energy, offering formulas and explaining their applications. The paragraph then moves on to simple harmonic motion, discussing the frequency and period of oscillations, and providing formulas for a mass-spring system. It concludes with a brief mention of the physical pendulum and resources for further learning on these and other physics topics.

Mindmap

Keywords

💡Displacement

Displacement refers to the change in position of an object and is a vector quantity, meaning it has both magnitude and direction. In the context of the video, it is calculated as the product of velocity and time (D = VT) and is crucial in understanding motion, particularly in kinematics problems involving constant speed or uniform motion.

💡Velocity

Velocity is a vector quantity that describes the rate of change of an object's position with respect to time, taking into account both speed and direction. The video emphasizes the difference between velocity and speed, noting that velocity can be positive or negative depending on the direction of motion, while speed is always positive. It is a fundamental concept in physics when discussing motion and is integral to the formulas presented in the video.

💡Acceleration

Acceleration is the rate of change of velocity with respect to time and is also a vector quantity. In the video, it is used to describe the change in velocity when an object is undergoing constant acceleration, such as in uniformly accelerated motion. The formula for final velocity in terms of initial velocity and acceleration (V_final = V_initial + a*t) is a key example of how acceleration is applied in physics problems.

💡Projectile Motion

Projectile motion refers to the motion of an object that is launched into the air and is influenced only by gravity. The video discusses how the kinematic formulas used for constant acceleration apply to projectile motion as well, with special attention to the horizontal and vertical components of motion. The concepts of maximum height and range are also explored within the context of projectile motion.

💡Relative Velocity

Relative velocity is the velocity of an object with respect to a reference point or another moving object. The video explains that it is calculated by subtracting the velocity of the reference object from the velocity of the object in question. This concept is important in understanding how objects move in relation to each other and is used to analyze complex motion scenarios.

💡Newton's Laws of Motion

Newton's Laws of Motion are three fundamental principles that describe the relationship between the motion of an object and the forces acting upon it. The video touches on all three laws, highlighting the concepts of inertia, net force, and action-reaction pairs. These laws are essential for understanding how forces affect motion and are foundational in physics.

💡Uniform Circular Motion

Uniform circular motion occurs when an object moves in a circular path at a constant speed. The video explains the concepts of centripetal acceleration and centripetal force, which are directed towards the center of the circle and are responsible for keeping the object in circular motion. The formulas for velocity, period, and centripetal force are discussed in relation to uniform circular motion.

💡Work and Energy

Work and energy are key concepts in physics related to the transfer and conservation of energy. The video defines work as the product of force and displacement, and energy as the capacity to do work. The work-energy theorem is introduced, stating that the net work done on an object is equal to the change in its kinetic energy. Additionally, potential energy and elastic potential energy are discussed, highlighting their roles in energy conservation.

💡Power

Power is defined as the rate at which work is done or energy is transferred. It is measured in watts and gives insight into how quickly work is performed. The video explains power in terms of work done over time and also relates it to force and velocity in the context of mechanical power. Understanding power is important for analyzing the efficiency and speed of energy transfer in various systems.

💡Momentum and Impulse

Momentum is the product of an object's mass and its velocity, and it is a vector quantity that describes the motion of the object. Impulse, on the other hand, is the product of force and the time over which the force acts. The video introduces the impulse-momentum theorem, which states that the change in momentum of an object is equal to the impulse applied to it. This theorem is fundamental in understanding how forces cause changes in motion.

💡Rotational Motion

Rotational motion involves an object spinning around an axis. The video explains several concepts related to rotational motion, such as angular displacement, angular velocity, and angular acceleration. It also discusses the relationship between linear quantities and rotational quantities, showing how formulas from linear kinematics can be applied to rotational motion. Understanding rotational motion is crucial in various physics scenarios, including the analysis of gears and flywheels.

Highlights

Introduction to common physics formulas for motion with constant speed.

Displacement (D) equals Velocity (V) times Time (T), highlighting the relationship between distance, speed, and time.

Explanation of the difference between speed and velocity, emphasizing that speed is a scalar quantity and velocity is a vector.

Formula for motion with constant acceleration, where final velocity (V_final) equals initial velocity (V_initial) plus acceleration (a) times time (T).

Displacement formula for constant acceleration, using average velocity, and its derivation from initial and final velocities.

Introduction to kinematics, including formulas for displacement and the concept of horizontal and vertical displacement.

Explanation of projectile motion, including the role of gravity as the sole force acting on the object and the trajectory of the projectile.

Formulas for maximum height and range of a projectile, demonstrating the application of kinematic equations in projectile problems.

Discussion on relative velocity, including the basic formula and its application in various scenarios.

Overview of Newton's laws of motion, detailing the principles that govern the behavior of objects in motion or at rest.

Explanation of forces, including weight, kinetic friction, and static friction, with their respective formulas.

Introduction to uniform circular motion, including formulas for centripetal acceleration, centripetal force, and velocity.

Work, energy, and power concepts, with formulas that describe the relationship between force, displacement, kinetic energy, and power.

Springs and elastic potential energy discussion, with formulas for force, spring constant, and elastic potential energy.

Momentum and impulse definitions, along with the impulse-momentum theorem and its applications.

Rotational motion formulas, highlighting the relationship between angular displacement, linear velocity, and angular velocity.

Torque and rotational work concepts, with formulas that connect torque to force and rotational work to angular displacement.

Gravitational force and gravitational acceleration formulas, explaining the attraction between two masses and the acceleration due to gravity.

Simple harmonic motion and pendulums discussion, including formulas for period, frequency, and elastic potential energy.

Transcripts

Browse More Related Video

Physics 1 Final Exam Review

AP Physics 1 - 10 Minute Recap

All IGCSE Physics Equations you need to know for the new syllabus

AP Physics C: Rotational Kinematics Review (Mechanics)

All Physics Formulas in One Go | Mindmap and Formula Sheet for Class 9 Science CBSE

Review of all concepts from AP Physics C mechanics 2020

Related Tags

Physics Formulas Kinematics Projectile Motion Relative Velocity Newton's Laws Uniform Circular Motion Work and Energy Springs and Elasticity Momentum and Impulse Rotational Motion