High School Physics - Resistance, Resistors, and Resistivity

Dan Fullerton
23 Dec 201108:30
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the concepts of electrical conductivity, resistivity, and resistance. It explains how these properties depend on the density and mobility of free charges in a material, and how they are affected by temperature. The script also covers the formula for calculating resistance, emphasizing the importance of a material's geometry. Examples are provided to illustrate how resistivity varies among different materials and how to calculate the resistance of a wire given its length and cross-sectional area.

Takeaways
  • 📌 Materials can be classified as conductors or insulators based on how freely they allow the movement of electrical charges.
  • 🔧 Conductivity (denoted by Greek letter Sigma) measures how easily charges move in a material, depending on the density and mobility of free charges.
  • ⚖️ Resistivity (denoted by Greek symbol Rho) is the material's ability to resist the flow of electric charge and is inversely related to conductivity.
  • 🌡️ Resistivity is not constant and typically increases with temperature for most materials.
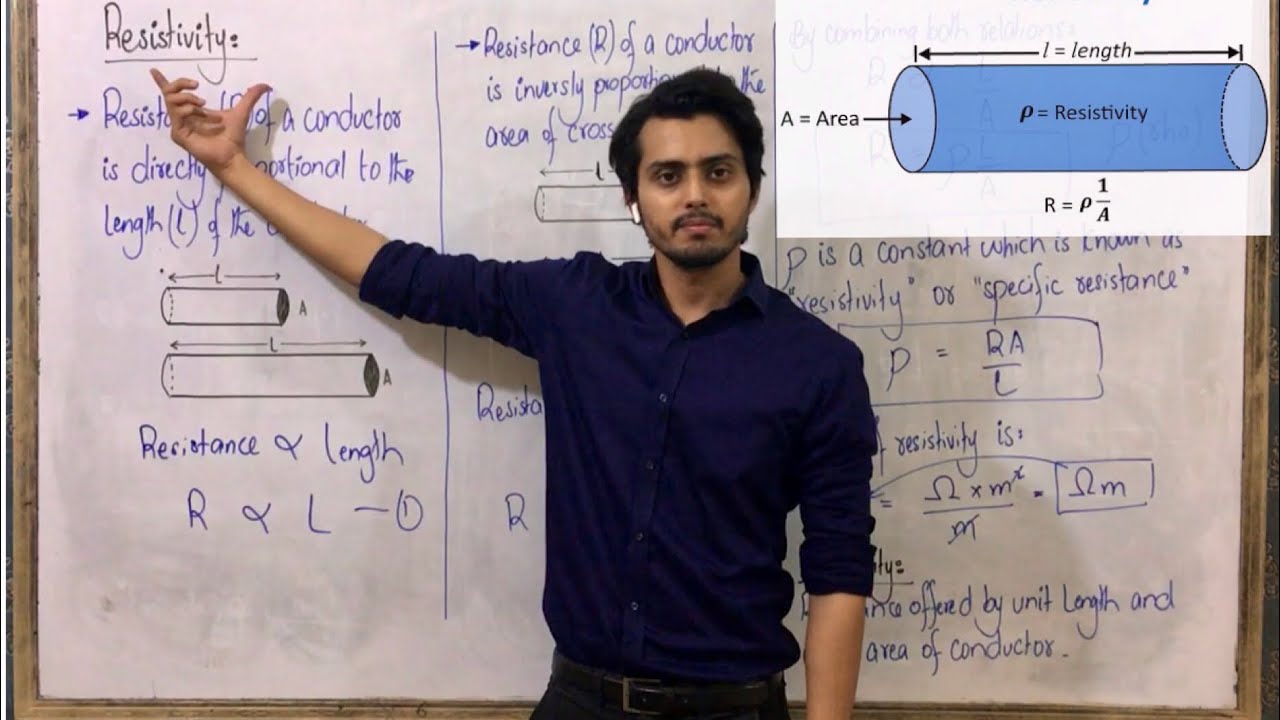
  • 🏗️ The resistance of a conductor (in ohms) is determined by its resistivity (Rho), length (L), and cross-sectional area (A), expressed as R = ρ * L / A.
  • 🔍 To find resistivity, one can rearrange the resistance formula: ρ = R * A / L.
  • 🔩 The shape and geometry of a resistor play a crucial role in its resistance, with longer lengths increasing resistance and larger cross-sectional areas decreasing it.
  • 📉 The electrical resistance of a metallic conductor is inversely proportional to its cross-sectional area.
  • 🏷️ Materials with the lowest resistivity are preferred for making efficient conductors, such as gold.
  • 📐 To calculate the length of a wire with given resistance and cross-sectional area, use the formula L = (R * A) / ρ.
  • 🔍 For a given resistance and cross-sectional area, the length of a copper wire can be determined by comparing it to a wire with known resistivity and length.
Q & A

  • What is the definition of conductivity?

    -Conductivity refers to the ability of a material to allow the free movement of electrical charges. It is represented by the Greek letter Sigma (σ) and depends on the density of free charges and the mobility of those charges within the material.

  • How are conductivity and resistivity related?

    -Conductivity (σ) and resistivity (ρ) are inversely related. The resistivity is the inverse of conductivity, mathematically expressed as ρ = 1/σ or σ = 1/ρ.

  • What are the units of resistivity?

    -The units of resistivity are ohms times meters (Ω·m), and it is represented by the Greek symbol Omega (Ω).

  • How does temperature affect resistivity in materials?

    -In most materials, resistivity increases as the temperature rises. This is because the increased thermal energy causes more scattering of charge carriers, impeding their flow.

  • What factors determine the resistance of a conductor?

    -The resistance of a conductor depends on its resistivity (ρ), its length (L), and its cross-sectional area (A). The formula for calculating resistance (R) is R = ρ * L / A.

  • How does the shape or geometry of a resistor affect its resistance?

    -The shape or geometry of a resistor, particularly its length and cross-sectional area, directly affects its resistance. A longer resistor will have more resistance, while a resistor with a larger cross-sectional area will have less resistance.

  • What is the relationship between the electrical resistance of a metallic conductor and its cross-sectional area?

    -The electrical resistance of a metallic conductor is inversely proportional to its cross-sectional area. A larger cross-sectional area results in lower resistance.

  • Which material has the least resistance among different conducting wires of the same length and diameter?

    -Gold has the least resistance among different conducting wires of the same length and diameter, with a resistivity of 2.44 * 10^-8 ohm·m at 20°C.

  • If a 1-meter long silver wire and a copper wire have the same resistance and cross-sectional area, how can you calculate the length of the copper wire?

    -Since the resistances are equal, you can set up the equation ρ_copper * L_copper / A = ρ_silver * L_silver / A. Knowing that ρ_silver and A are constants, you can solve for L_copper by rearranging the equation to L_copper = (ρ_silver * L_silver) / ρ_copper.

  • Given a 10-meter length copper wire at 20°C with a radius of 1 * 10^-3 meters, how do you find its cross-sectional area and resistance?

    -The cross-sectional area (A) of a wire is given by the formula A = π * r^2, where r is the radius. So, A = π * (1 * 10^-3)^2 ≈ 3.14 * 10^-6 m^2. The resistance (R) can then be calculated using R = ρ * L / A, where ρ is the resistivity of copper at 20°C (1.72 * 10^-8 ohm·m), L is the length (10 m), and A is the cross-sectional area (3.14 * 10^-6 m^2). Plugging in the values gives R ≈ 5.5 * 10^-2 ohms.

  • What is the significance of understanding the relationship between resistivity, conductivity, and resistance in material science and electrical engineering?

    -Understanding the relationship between resistivity, conductivity, and resistance is crucial in material science and electrical engineering for designing and optimizing electrical components such as resistors, wires, and electronic devices. It allows engineers to predict and control how materials will behave under different conditions, ensuring efficiency, safety, and longevity of electrical systems.

Outlines
00:00
🔬 Introduction to Conductivity and Resistivity

This paragraph introduces the concepts of conductivity and resistivity, defining them and explaining their relationship. Conductivity, represented by the Greek letter Sigma, measures how easily charges can move through a material, depending on the density and mobility of free charges. Resistivity, symbolized by the Greek letter Rho, is the material's ability to resist the flow of electric charge and is inversely related to conductivity. The units for resistivity are ohms times meters (ohm·m). The paragraph also discusses how resistivity can change with temperature and the importance of a material's geometry in determining its resistance.

05:03
🧮 Calculation of Resistivity from Given Resistance

This section focuses on the practical application of the resistance formula to calculate the resistivity of a material. Given the resistance of a wire, its length, and cross-sectional area, the paragraph walks through the process of solving for resistivity using the formula R = ρ(L/A). It provides an example where a 3.5 M length wire with a specific cross-sectional area at 20°C has a resistance of 0.625 ohms, leading to the calculation of the wire's resistivity as 5.6 * 10^-8 ohm·m.

🔍 Comparing Resistivities of Different Materials

This part of the script discusses the qualitative aspect of comparing resistivities of different materials at a constant temperature. It explains that the resistivity of a metallic conductor is inversely proportional to its conductivity. The paragraph uses a table of resistivities at 20°C to illustrate which material, among several options, would have the least resistance when all other factors are equal. Gold is identified as having the lowest resistivity, hence the least resistance.

📏 Determining Length of Copper Wire with Equivalent Resistance

The paragraph presents a problem-solving scenario where the length of a copper wire is calculated given that it has the same resistance as a 1 M long silver wire with the same cross-sectional area. By setting up an equation based on the resistance formula and solving for the unknown length, the paragraph demonstrates the relationship between resistivity, length, and area in determining the resistance of a conductor. The calculated length of the copper wire is approximately 0.924 M.

🔍 Calculating Cross-Sectional Area and Resistance of a Copper Wire

This section involves calculating the cross-sectional area and resistance of a 10 m long copper wire with a given radius at 20°C. The area is determined using the formula for the area of a circle (πr²), and the resistance is calculated using the resistivity of copper from a reference table, the wire's length, and the newly found cross-sectional area. The final calculated resistance for the copper wire is approximately 5.5 * 10^-2 ohms.

Mindmap
Keywords
💡Conductivity
Conductivity, represented by the Greek letter Sigma (σ), is a measure of a material's ability to allow the flow of electric current. It depends on the density of free charges within the material and their mobility. High conductivity indicates that the material allows charges to move freely, making it a good conductor of electricity. In the context of the video, this property is crucial for understanding how well a material can conduct electricity, which is the main focus of the discussion.
💡Resistivity
Resistivity, symbolized by the Greek letter Rho (ρ), is the property of a material that quantifies how strongly it resists the flow of electric current. It is the inverse of conductivity, meaning that materials with high resistivity have low conductivity and vice versa. Resistivity is affected by factors such as temperature, with most materials showing an increase in resistivity as temperature rises. In the video, resistivity is a central concept used to explain how materials can impede the flow of electric charge.
💡Resistance
Resistance is the opposition a material offers to the flow of electric current. It is a property that depends on the material's resistivity, its shape (geometry), and its dimensions. The formula for calculating resistance (R) is given by resistivity (ρ) times the length (L) of the conductor, divided by its cross-sectional area (A). Resistance is measured in ohms (Ω). In the video, the concept of resistance is used to demonstrate how the physical properties of a conductor can affect its ability to impede electric current.
💡Electric Charges
Electric charges are the fundamental particles that make up the electric current. They can be positive, negative, or neutral. In the context of the video, the movement of electric charges through a material is what constitutes an electric current. The ease with which these charges can move is determined by the material's conductivity, while the opposition to their movement is described by resistivity and resistance.
💡Ohms
Ohms (Ω) is the unit of measurement for electrical resistance. It quantifies the magnitude of resistance a material offers to the flow of electric current. The concept is central to the video as it is used to express both resistivity and resistance values, and it is essential for understanding how materials interact with electric currents.
💡Cylindrical Resistor
A cylindrical resistor is a component designed to provide a specific amount of resistance in an electrical circuit. Its resistance is determined by its geometry, specifically its length and cross-sectional area. The video uses the example of a cylindrical resistor to illustrate how changes in these dimensions can affect the overall resistance of the conductor.
💡Temperature
Temperature plays a significant role in the electrical properties of materials. Generally, as the temperature of a material increases, its resistivity also increases, leading to a higher resistance to electric current. This relationship is important in the design and analysis of electrical components, as it can affect their performance under varying temperature conditions.
💡Geometry
In the context of the video, geometry refers to the shape and structure of an object, specifically a resistor. The geometry of a resistor affects its resistance, with factors such as length and cross-sectional area being crucial in determining how much the resistor opposes the flow of electric current. The term is used to describe how the physical form of a conductor influences its electrical properties.
💡Cross-Sectional Area
The cross-sectional area of a conductor, such as a wire, is the internal area perpendicular to the direction of the current flow. This area is important in determining the resistance of the conductor, as a larger cross-sectional area results in lower resistance, allowing more current to flow through. The cross-sectional area is a key factor in the design of electrical components, as it directly affects their performance and efficiency.
💡Resistivities of Materials
Resistivities of materials refer to the inherent properties of different substances that determine how much they resist the flow of electric current. These values are typically constant for a given material at a specific temperature and are used to compare the electrical conductive properties of various materials. In the video, a table of resistivities at 20°C for different materials is used to illustrate which materials are better conductors or insulators.
💡Electrical Resistance of Metallic Conductors
The electrical resistance of metallic conductors is a measure of how much they oppose the flow of electric current. This resistance is influenced by the material's resistivity, its geometry, and other factors like temperature. Metallic conductors are materials that allow electric charges to move relatively freely, making them suitable for use in electrical wiring and components.
Highlights

The definition of conductivity and resistivity is introduced, explaining their relationship and significance in electrical science.

Conductivity is symbolized by the Greek letter Sigma and depends on the density of free charges and the mobility of those charges.

Resistivity is symbolized by the Greek letter Omega and is the inverse of conductivity, with units of ohms times meters.

The impact of temperature on resistivity is discussed, noting that resistivity typically increases with temperature.

Resistance is defined as an object's ability to resist the flow of electric charge, and its calculation involves resistivity, length, and cross-sectional area.

The geometry of an object, such as a cylindrical resistor, plays a crucial role in determining its resistance.

A practical example is given to calculate the resistivity of a wire using its resistance, length, and cross-sectional area.

The concept that the electrical resistance of a metallic conductor is inversely proportional to its cross-sectional area is explained.

A table of resistivities at 20°C for different materials is referenced to discuss the least resistance among materials of the same length and diameter.

The problem of calculating the length of a copper wire given the resistance and length of a silver wire with the same cross-sectional area is solved.

The method for determining the cross-sectional area and resistance of a copper wire with a given length and radius is outlined.

The resistivity of various materials at 20°C is used to calculate the resistance of a copper wire with known dimensions.

The importance of understanding the relationship between resistivity, conductivity, and resistance for designing functional objects like resistors is emphasized.

The transcript concludes with an encouragement for further exploration of the topic and a recommendation for additional resources.

Transcripts

Browse More Related Video

Resistivity | Specific Resistance | Easier Explanation

Resistivity - A-level Physics

A Level Physics: What is resistivity?

Resistivity and conductivity | Circuits | Physics | Khan Academy

Resistance of a Conductor | Electricity and Circuits | Don't Memorise

Resistivity - A Level Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
ElectricalPropertiesConductorsInsulatorsPhysicsEducationProblemSolvingMaterialScienceOhm'sLawCircuitAnalysisTemperatureEffectsResistorCalculationsMetallicConductors