Resistivity - A Level Physics

Physics Online
20 May 201503:01
EducationalLearning
32 Likes 10 Comments

TLDRThe video script explains the concept of electrical resistance in a metal lattice, highlighting how resistance is directly proportional to the length of the conductor and inversely proportional to its cross-sectional area. It introduces the notion of resistivity, specific to each material, and dependent on temperature. The resistivity is visualized as the resistance of a cubic meter of a substance, with variations among different metals and an increase with temperature.

Takeaways
  • πŸ“ Resistance in a conductor is proportional to its length, meaning longer conductors offer more resistance to electrons.
  • πŸ”„ Vibration and movement of electrons within the metal lattice create resistance as they pass through.
  • πŸ“ If the length of the conductor is doubled, the resistance increases by a factor of two due to more obstacles for the electron to overcome.
  • πŸ“¦ Wider conductors provide more pathways for electrons, reducing resistance as the current has more options to follow the path of least resistance.
  • πŸ”„ The resistance is inversely proportional to the cross-sectional area, meaning larger areas result in lower resistance.
  • 🌐 The resistivity (Rho) of a material is a constant specific to that material and is affected by temperature.
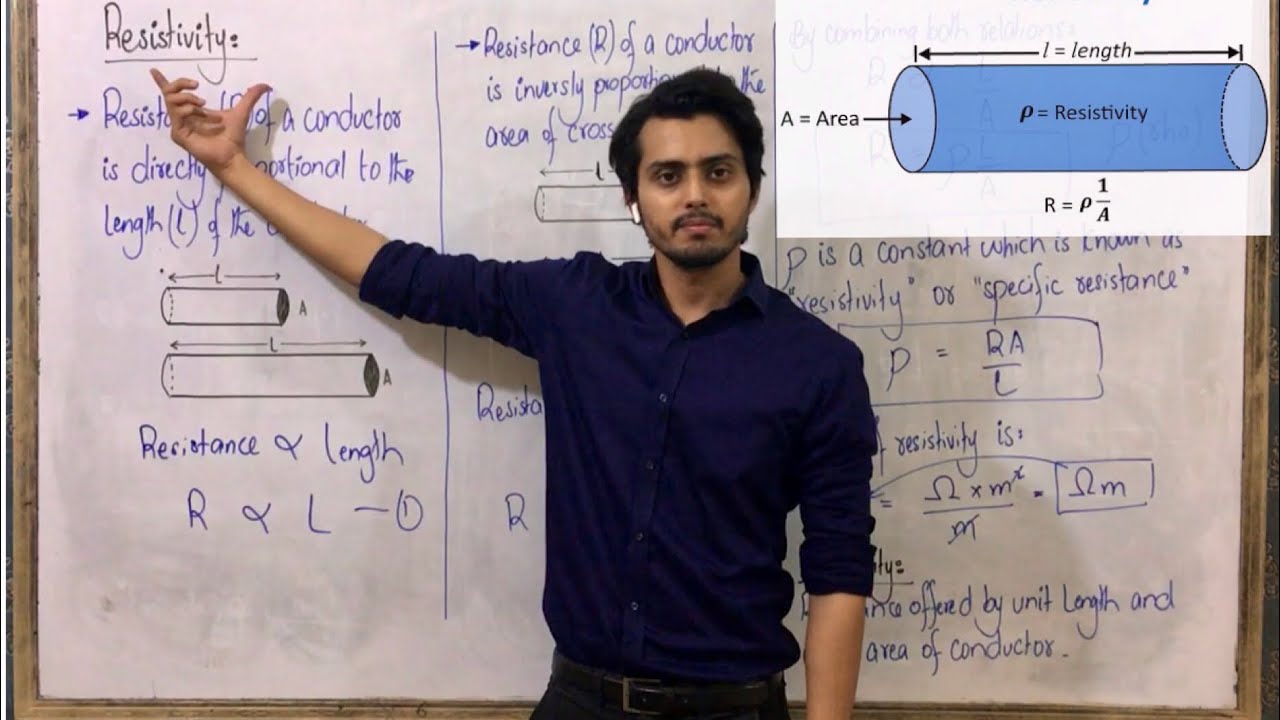
  • 🎯 Resistivity can be calculated using the formula: R = Rho * L / A, where R is resistance, L is length, and A is area.
  • πŸ“Œ The unit of resistivity is ohm-meters (Ω·m), derived from the units of resistance (ohms), length (meters), and area (meters squared).
  • πŸ”† The resistivity of a material can be visualized as the resistance offered by a cubic meter of that substance.
  • 🌑️ Changes in temperature affect resistivity, causing it to increase with rising temperature in most metals.
Q & A

  • How does the vibration of a metal lattice affect electron movement?

    -The vibration of a metal lattice creates a resistance to the movement of electrons as they have to navigate through the vibrations, which can impede their progress. This is due to the lattice offering a discrete resistance to dislocation motion in a pure crystalline material where diffusion is not significant.

  • What is the relationship between the length of a conductor and its resistance?

    -The resistance of a conductor is directly proportional to its length. If the length of the conductor is doubled, the resistance also doubles because the electrons have to travel a longer path, encountering more collisions and resistance.

  • How does the cross-sectional area of a conductor influence its resistance?

    -The resistance of a conductor is inversely proportional to its cross-sectional area. A larger cross-sectional area provides more pathways for the electrons to flow, reducing the overall resistance.

  • What is the formula for calculating electrical resistance in terms of resistivity, length, and area?

    -The formula for calculating electrical resistance (R) is given by R = ρ * L / A, where ρ (rho) is the resistivity of the material, L is the length of the conductor, and A is its cross-sectional area.

  • What is resistivity, and how does it vary with different materials and temperature?

    -Resistivity (ρ) is an intrinsic property of a material that quantifies how strongly the material opposes the flow of electric current. It is specific to the type of material and its temperature. For example, the resistivity of copper will be different from that of steel or aluminum, and it will change with variations in temperature.

  • What are the units for resistivity, and how are they derived from the formula?

    -The units for resistivity are ohm meters (Ω·m). This is derived from the units in the resistance formula where resistance is in ohms (Ω), the area (A) is in square meters (m²), and the length (L) is in meters (m), resulting in the unit of ohm meter for resistivity (ρ = R * A / L).

  • How does temperature affect the resistivity of a material?

    -Temperature generally causes the resistivity of a material to increase. As temperature rises, the lattice vibrations intensify, leading to more frequent collisions between electrons and lattice atoms, thereby increasing the resistance to electron flow.

  • What is the role of lattice vibrations in the electrical resistivity of metals?

    -Lattice vibrations interact with free electrons in a conducting solid, contributing to electrical resistance. These vibrations are a form of normal modes of lattice motion, and they can scatter electrons, impeding their flow and thus increasing the resistivity of the metal.

  • How does the concept of a 'path of least resistance' relate to the cross-sectional area of a conductor?

    -The 'path of least resistance' concept suggests that when a conductor has a larger cross-sectional area, electrons have more options to choose from for their path through the conductor. This reduces the likelihood of collisions and resistance, effectively lowering the overall resistance of the conductor.

  • What is an example of how resistivity varies with temperature in a specific material?

    -In the A15 superconducting class, the resistivity (ρ) is proportional to the square of the temperature (T^2) from the critical temperature (Tc) up to about 50 K. This indicates that the resistivity increases with temperature, following the relationship ρ ∝ T^2.

  • How does the resistivity of a cubic meter of a metal substance change with temperature?

    -The resistivity of a cubic meter of a metal substance, such as copper, will vary with temperature. As the temperature increases, the resistivity also increases due to enhanced lattice vibrations and electron scattering, leading to higher resistance to the flow of electric current.

Outlines
00:00
πŸ”Œ Understanding Electrical Resistance in Metals

This paragraph discusses the concept of electrical resistance in a metallic lattice model. It explains how an electron moving through the metal lattice experiences resistance, which increases with the length of the conductor. The analogy of a longer conductor having more obstacles for the electron to overcome is used to illustrate that resistance is proportional to the length of the conductor. The paragraph then explores the effect of the cross-sectional area on resistance, stating that a larger area provides more paths of least resistance, thus reducing overall resistance. It is indicated that resistance is inversely proportional to the area. The paragraph concludes by introducing the resistivity (denoted by the Greek letter rho) as a material-specific constant that depends on the type of metal and its temperature. The resistivity equation (R = ρL/A) is presented, with units of ohm meters, and a practical example of a cubic meter of metal is used to visualize resistivity, which varies among different metals and increases with temperature.

Mindmap
Keywords
πŸ’‘Metal Lattice
A metal lattice refers to the regular arrangement of atoms or ions in a metallic solid, forming a crystal structure. In the context of the video, the lattice is the environment through which an electron must travel, and its vibrations can create resistance for the electron. This is a crucial concept as it sets the stage for understanding electrical resistance in metallic conductors.
πŸ’‘Vibration
Vibration in the context of the video refers to the movement of atoms or ions within the metal lattice. These vibrations can impede the progress of an electron moving through the lattice, thus contributing to the resistance experienced by the electron. It is a fundamental concept in understanding how a conductor's physical state can affect its electrical properties.
πŸ’‘Electron
An electron is a subatomic particle with a negative charge that orbits the nucleus of an atom. In the context of the video, electrons are the charge carriers that move through a metal lattice, and their movement is impeded by the lattice's vibrations, leading to electrical resistance. Understanding the role of electrons is essential for grasping how metals conduct electricity.
πŸ’‘Resistance
Resistance is the opposition that a material offers to the flow of electric current. In the video, resistance is a result of the electron's interaction with the vibrating metal lattice and is directly proportional to the length of the conductor and inversely proportional to its area. This key concept is central to understanding the behavior of conductors in electrical circuits.
πŸ’‘Conductor
A conductor is a material that allows the flow of electric current with minimal resistance. In the video, the metal lattice serves as a conductor, and the properties of this conductor, such as length and area, directly influence the resistance it offers to the flow of electrons. Understanding conductors is vital for analyzing and designing electrical systems.
πŸ’‘Resistivity
Resistivity is a property of a material that quantifies how strongly it resists the flow of electric current. It is specific to the material and its temperature and is denoted by the Greek letter rho (ρ). In the video, resistivity is introduced as a constant of proportionality that relates resistance (R) to the length (L) and area (A) of the conductor.
πŸ’‘Length
Length, in the context of the video, refers to the distance an electron must travel through a conductor. It is a factor in the calculation of resistance, with the video explaining that resistance is directly proportional to the length of the conductor. This means that longer conductors will have higher resistance, which is a fundamental concept in understanding how electrical resistance behaves in different scenarios.
πŸ’‘Area
Area, as discussed in the video, refers to the cross-sectional area of a conductor through which the electric current flows. It is inversely proportional to resistance, meaning that a larger area results in lower resistance. This concept is important for understanding how the geometry of a conductor affects its electrical properties.
πŸ’‘Temperature
Temperature is a measure of the average kinetic energy of the particles in a substance and plays a significant role in determining the resistivity of a material. In the video, it is mentioned that resistivity is specific to a certain kind of material and temperature, indicating that changes in temperature can affect a material's resistance to electric current.
πŸ’‘Ohm
The ohm is the unit of electrical resistance in the International System of Units (SI). It is named after the German physicist Georg Simon Ohm. In the video, the unit of resistance is given in ohms, and the unit for resistivity is ohm meters, which is derived from the formula for resistivity.
πŸ’‘Cubic Meter
A cubic meter is a unit of volume in the metric system, equivalent to the volume of a cube with edges one meter long. In the video, the concept of a cubic meter is used to visualize resistivity, with the example of a cube of metal being used to illustrate how resistivity can be thought of as the resistance of a volume of a substance.
Highlights

The model of a metal lattice and its vibration is introduced as a basis for understanding electron movement.

Electrons experience resistance when moving through a metal lattice due to vibrations.

The resistance an electron encounters is proportional to the length of the conductor it traverses.

Doubling the length of the conductor results in doubling the resistance due to more obstacles for the electron.

The resistance is inversely proportional to the area of the conductor, allowing more paths for the electron to choose.

A larger cross-sectional area provides more options for the path of least resistance, reducing overall resistance.

The resistivity (rho) of a material is a constant that depends on the type of material and temperature.

Resistivity is specific to a certain material and can be different for copper, steel, aluminum, etc.

The equation for resistance is given as R = rho * L / A, where R is resistance, rho is resistivity, L is length, and A is area.

The unit for resistivity is the ohm meter, derived from the units of resistance (ohms) and area (meters squared).

A cube of metal with one meter dimensions can be used to visualize resistivity as the resistance of a cubic meter of the substance.

Resistivity varies from metal to metal and is affected by temperature, increasing as temperature rises.

The concept of resistance being proportional to length and inversely proportional to area is crucial for understanding conductor behavior.

The model demonstrates the importance of conductor dimensions in determining the overall resistance encountered by electrons.

The discussion on resistivity provides a fundamental understanding of material properties affecting electron flow.

The practical application of this understanding can lead to better material selection and design in electrical engineering.

The relationship between resistivity, length, and area provides a comprehensive framework for analyzing and predicting resistance in conductors.

Transcripts

Browse More Related Video

Resistance of a Conductor | Electricity and Circuits | Don't Memorise

A Level Physics: What is resistivity?

Resistivity | Specific Resistance | Easier Explanation

High School Physics - Resistance, Resistors, and Resistivity

Resistivity - A-level Physics

Resistivity and Resistance Formula, Conductivity, Temperature Coefficient, Physics Problems

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
ElectricalResistanceMetalPropertiesResistivityExplainedPhysicsConceptsMaterialScienceTemperatureEffectsElectronFlowOhmicMeasurementEngineeringInsightsEducationalContent