AP Physics Workbook 6.D Measuring Spring Constants
TLDRThe video script discusses methods to determine the spring constant without measuring time. Two approaches are highlighted: one using the displacement of the spring with known masses and the other utilizing the oscillation period by timing oscillations. The script also explores how these methods would be affected if conducted on a different planet with higher gravity, concluding that while measurements might differ, the calculated spring constant would remain the same due to its independence from gravitational force.
Takeaways
- 📚 The topic is AP Physics, focusing on Unit 6 about simple harmonic motion and measuring the spring constant.
- 🔍 Students Jellico and Blake are tasked with determining the spring constant of a given spring without using a stopwatch.
- 📈 Angelica's method involves measuring the displacement of the spring with known masses and using Hooke's Law (K = Fg/X1).
- 🎢 Blake's method requires timing the oscillations of the spring with different masses to find the period and calculate K (K = 4π²m/T²).
- 📏 A meter stick is available for measuring displacement, but no access to a stopwatch or other timing devices.
- 🔄 The experiment should be repeated with different masses to reduce error and increase accuracy in determining the spring constant.
- 🌌 A hypothetical scenario involves conducting the experiment on a different planet with higher gravity, affecting the force of gravity (FG) component.
- 🌍 On a new planet, Angelica's method might yield different displacement measurements due to the altered force of gravity, but the spring constant remains the same.
- 🚀 Blake's calculation is unaffected by the change in gravity since it relies on the mass and the period of oscillation, both of which are independent of gravity.
- 📊 Graphing the force of gravity versus displacement or mass versus period squared will yield the spring constant through the slope of the line.
- 🔍 Understanding Hooke's Law and simple harmonic motion formulas is crucial for accurately determining the spring constant in various conditions.
Q & A
What is the main topic of the video?
-The main topic of the video is the determination of the spring constant using two different methods, without the need for a stopwatch or measuring time directly.
What is the scenario presented in the video?
-The scenario involves two students, Jellico and Blake, who are given a spring and asked to determine its spring constant. They have access to a stand, known masses, a meter stick, but no access to a stopwatch or other time-measuring devices.
How can the spring constant be calculated without measuring time?
-The spring constant can be calculated by measuring the displacement of the spring for different known masses and using Hooke's Law, which states that the force exerted by the spring is proportional to the displacement (F = kx), where k is the spring constant and x is the displacement.
What is the formula for the spring constant based on the force of gravity and displacement?
-The spring constant can be calculated using the formula k = F_gravity / x, where F_gravity is the force of gravity acting on the mass and x is the displacement of the spring.
How can the spring constant be determined using the period of oscillation?
-The spring constant can be determined using the formula T^2 = (4π^2m) / k, where T is the period of oscillation, m is the mass, and k is the spring constant. By graphing T^2 against m, the slope of the line will give the value of k.
What would happen if the experiment is conducted on a different planet with a higher gravity?
-On a planet with higher gravity, the force of gravity (F_gravity) would be different, leading to a larger displacement of the spring. However, the period of oscillation (T) would remain unchanged, and thus Blake's method of calculating the spring constant would yield the same result. Angelica's method might give different numerical values due to the change in F_gravity, but the ratio used to calculate the spring constant would remain the same.
How does the method of calculating the spring constant change when only a stopwatch is available?
-When only a stopwatch is available, one can measure the period of oscillation for different masses and use the formula T^2 = (4π^2m) / k to calculate the spring constant. By graphing the period squared (T^2) against the mass (m), the slope of the resulting line will give the value of k.
What is the significance of the spring constant being the same on different planets?
-The spring constant is a measure of the stiffness of the spring and is independent of the force of gravity. Therefore, it remains the same regardless of the planet on which the experiment is conducted, as long as the spring and the masses used are the same.
How can errors be reduced in the spring constant measurement?
-Errors can be reduced by repeating the experiment with different masses and averaging the results. This helps to account for any inconsistencies or variations in the measurements.
What is the relationship between the force of gravity and the displacement of the spring?
-The force of gravity (F_gravity) is directly proportional to the mass (m), and the displacement (x) of the spring is directly proportional to the force exerted by the spring. Therefore, a stronger force of gravity on a different planet would result in a larger displacement, but the ratio of force to displacement (which determines the spring constant) remains constant.
What is the role of Hooke's Law in determining the spring constant?
-Hooke's Law states that the force exerted by a spring is proportional to its displacement, which is the basis for determining the spring constant. By measuring the force (due to gravity) and the displacement, one can calculate the spring constant using the formula k = F / x.
Outlines
📚 Introduction to Spring Constant Measurement
This paragraph introduces the topic of measuring the spring constant as part of an AP Physics workbook solution. It sets the scene where two students, Jellico and Blake, are tasked with determining the spring constant of a given spring. The challenge lies in the lack of access to a stopwatch or other timing devices, prompting the need for alternative methods to measure the spring constant. The paragraph outlines a method involving the displacement of the spring due to a known mass and the use of Hooke's Law to calculate the spring constant without the need for time measurement.
🕒 Measuring Spring Constant with Time Component
This paragraph discusses an alternative approach to measuring the spring constant, which involves the use of a stopwatch. With the introduction of a time component, the method relies on measuring the period of oscillation of the spring with different masses. The paragraph explains that by squaring the period and graphing it against the mass, the slope of the resulting line will yield the spring constant. This method is distinct from the previous one as it incorporates the element of time, which was not considered in the initial scenario.
🌌 Effects of Different Planet's Gravity on Spring Constant Measurement
This paragraph explores the impact of varying gravitational forces on the spring constant measurement. It hypothetically transfers the experimental setup to a different planet with a higher gravitational pull than Earth. The paragraph explains that while the force of gravity and the spring's displacement would change due to the different gravitational force, the spring constant would remain the same. This is because the spring's stiffness and the oscillation period are independent of gravity. The paragraph concludes that Blake's method, which relies on the oscillation period, would yield the same spring constant on any planet, while Angelica's method might yield different results due to the change in gravitational force, but ultimately, the spring constant would still be the same.
📈 Understanding Simple Harmonic Motion for Spring Constant Calculation
The final paragraph delves deeper into the application of simple harmonic motion in calculating the spring constant. It emphasizes the importance of understanding the relationship between the period of oscillation, the mass, and the spring constant. The paragraph clarifies that while the methods for measuring the spring constant may differ, the underlying principles remain the same. It suggests using the simple harmonic motion formula to derive the period and further refine the spring constant measurement. The paragraph concludes with a reminder that the spring's properties and the mass are key factors in determining the spring constant, regardless of external conditions such as gravity.
Mindmap
Keywords
💡Simple Harmonic Motion
💡Spring Constant
💡Hooke's Law
💡Displacement
💡Equilibrium
💡Free Body Diagram
💡Graph
💡Period
💡Acceleration Due to Gravity
💡Measurement
💡Stiffness
Highlights
The topic of discussion is the determination of the spring constant using simple harmonic motion principles.
The scenario involves two students, Jellico and Blake, tasked with determining the spring constant of a given spring.
The spring constant can be calculated without measuring time, using the displacement of the spring and the force of gravity acting on known masses.
A meter stick is available for measuring displacement, but no access to a stopwatch or other time-measuring devices.
An example is provided where a 10 kg mass is hung from the spring, displacing it by 0.40 meters at equilibrium.
At equilibrium, the force of the spring equals the force of gravity, allowing for the calculation of the spring constant using the formula K = (mg) / X1, where X1 is the displacement.
Graphing the force of gravity (FG) versus the displacement (X1) yields a straight line whose slope represents the spring constant (K).
To reduce experimental error, the mass-stretch experiment should be repeated with different masses.
If a stopwatch becomes available but the meter stick is not, Blake can measure the spring constant using the period of oscillation.
The period (T) of oscillation can be determined by counting the number of oscillations in one second, which can be used to calculate the spring constant.
The formula T^2 = 4PI^2 / (mK) can be used to graph the period squared (T^2) against mass (m), with the slope yielding the spring constant (K).
The experiment's setup involves hanging the spring vertically, stretching it, and then releasing it to oscillate, counting the oscillations within a given time frame.
The spring constant remains constant across different planets, as it is independent of the local gravitational force.
The method involving the period of oscillation (T) is unaffected by changes in gravity, as it relies solely on the mass and the spring's stiffness.
The displacement method (using force of gravity and displacement) will yield different results on a planet with a different gravitational force, as the spring will stretch more or less depending on the gravity.
Despite the differences in measured values due to gravity, the calculated spring constant will remain the same on Earth and on another planet.
The ratio of the force of gravity to displacement remains constant even on a different planet, as both values change proportionally.
Investigating the spring constant can start with Hooke's law and compare the results obtained from the two different methods.
The spring constant can be estimated using the formula for the period of simple harmonic motion, which requires the period and mass.
The period can also be derived from the force of gravity, offering alternative calculations for determining the spring constant.
Understanding the method that does not require time measurement is crucial for experiments where time measurement is not possible.
The spring undergoing simple harmonic motion provides a clear demonstration of the relationship between the spring constant, mass, and displacement.
Transcripts
Browse More Related Video
AP Physics Workbook 2.O Spring Force and Acceleration

8.01x - Lect 10 - Hooke's Law, Springs, Pendulums, Simple Harmonic Motion

2022 AP Physics 1 Free Response #5
AP Physics Workbook 6.L Sine function of SHM

Intro to springs and Hooke's law | Work and energy | Physics | Khan Academy
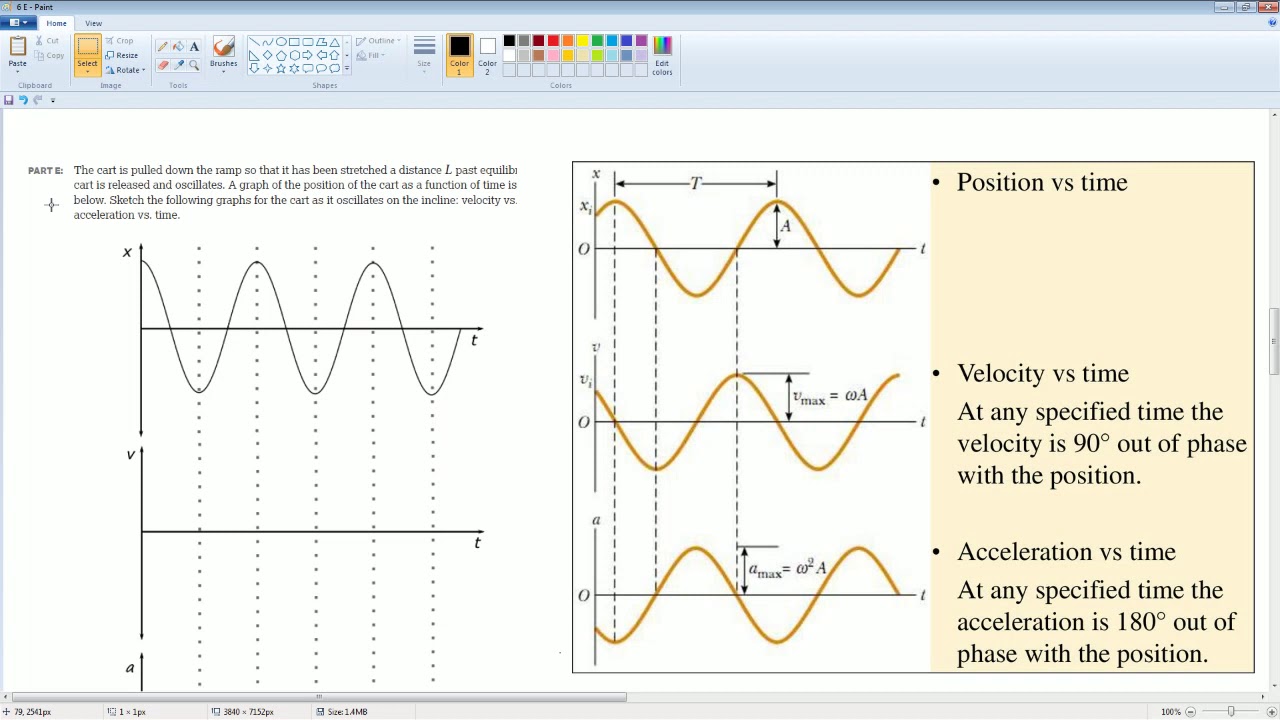
AP Physics Workbook 6.E Equilibrium on an Incline
5.0 / 5 (0 votes)
Thanks for rating: