Parallel and Perpendicular Lines, Transversals, Alternate Interior Angles, Alternate Exterior Angles

The Organic Chemistry Tutor

25 Jul 201741:56

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video script introduces fundamental concepts of geometry, focusing on lines and angles. It explains parallel and perpendicular lines, detailing how to calculate slopes for perpendicular lines and the properties of parallel lines intersected by a transversal. The script further discusses various types of angles, including interior, exterior, alternate, corresponding, consecutive, vertical, complementary, and supplementary angles, providing formulas and examples to illustrate their relationships and calculations. The video aims to enhance the viewer's understanding of these geometric principles through clear explanations and practical problem-solving.

Takeaways

📐 Parallel lines (A || B) never intersect and have the same slope.
🔍 Perpendicular lines intersect at a right angle (90°), denoted by the symbol ⊥.
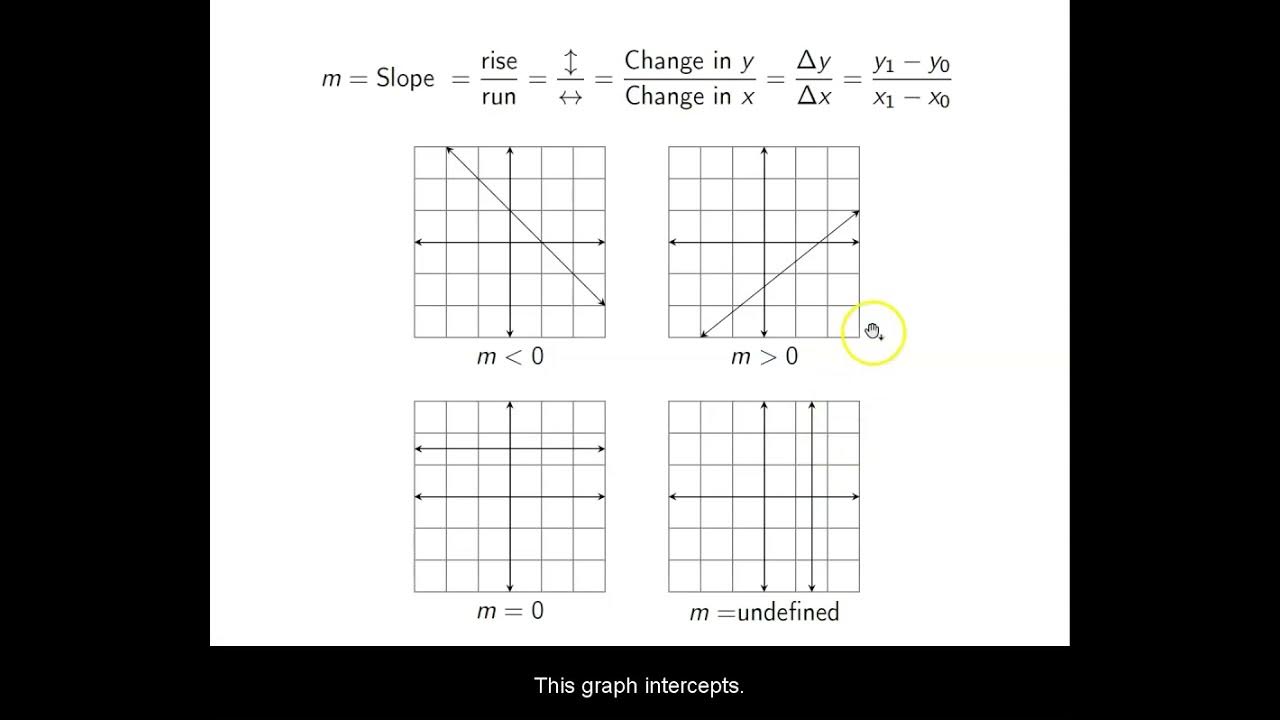
🔄 The slope of a line perpendicular to one with a slope of m/n is -n/m.
🔽 A transversal intersecting two parallel lines creates interior and exterior angles.
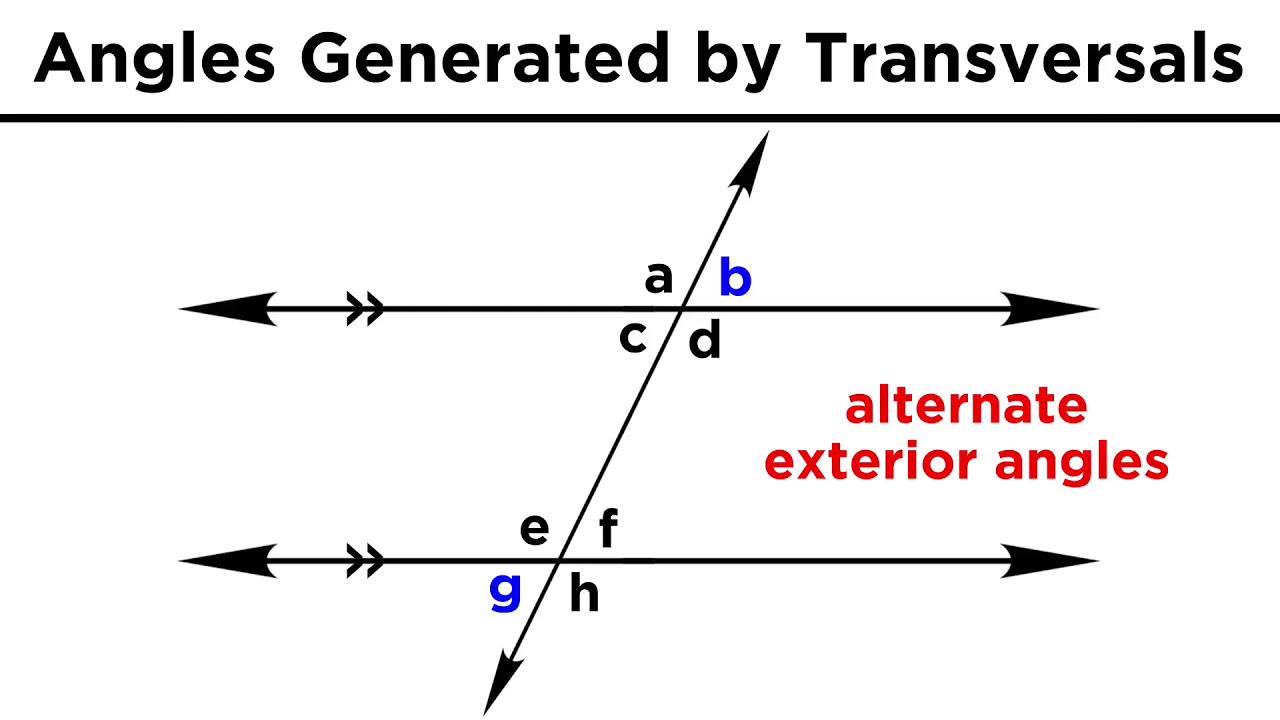
🔄 Alternate interior angles (between the two parallel lines) are congruent.
🔽 Exterior angles (outside the parallel lines) are congruent and form straight lines.
🔄 Corresponding angles (same position on parallel lines) are congruent.
🔽 Consecutive interior angles (on the same side of the transversal) are supplementary, adding up to 180°.
🔄 Vertical angles (formed by two intersecting lines) are congruent.
🔄 Complementary angles add up to 90°, while supplementary angles add up to 180°.
📊 The sum of interior angles of a triangle is 180°, and for a quadrilateral, it's 360°.
🔍 Solving for unknown angles in geometric configurations often involves setting up and solving equations based on angle relationships.

Q & A

What is the definition of parallel lines?
-Parallel lines are lines in a plane that do not intersect or meet; they are always the same distance apart and share the same slope.
How do you determine if two lines are perpendicular?
-Two lines are perpendicular if they intersect at a right angle, which is 90 degrees.
What is the relationship between the slopes of two perpendicular lines?
-The slopes of two perpendicular lines are negative reciprocals of each other. If one line has a slope of m, the other line's slope will be -1/m.
What are alternate interior angles and how do they relate to parallel lines?
-Alternate interior angles are the angles that are on opposite sides of a transversal intersecting two parallel lines. They are congruent, meaning they have the same measure.
What are corresponding angles and how do they compare on parallel lines?
-Corresponding angles are angles that occupy the same relative position on each of the two parallel lines intersected by a transversal. They are congruent, meaning they have the same measure.
How do consecutive interior angles differ from alternate interior angles?
-Consecutive interior angles are the angles that are on the same side of a transversal and next to each other. They are supplementary, meaning they add up to 180 degrees, whereas alternate interior angles are on opposite sides of the transversal and are congruent.
What is the definition of vertical angles?
-Vertical angles are the angles opposite each other when two lines intersect. They are congruent, meaning they have the same measure.
What are complementary angles and how do they relate to each other?
-Complementary angles are two angles whose measures add up to 90 degrees. They are two angles that together form a right angle.
What are supplementary angles and what is their sum?
-Supplementary angles are two angles whose measures add up to 180 degrees. They together form a straight line.
How can you find the sum of interior angles of a polygon?
-The sum of interior angles of a polygon can be found using the formula (n - 2) * 180, where n is the number of sides of the polygon.
What is the relationship between angles formed by two transversals intersecting two parallel lines?
-When two transversals intersect two parallel lines, they form various types of angles including alternate interior angles (congruent), consecutive interior angles (supplementary), and corresponding angles (congruent). The angles also follow the properties of vertical angles being congruent and supplementary angles adding up to 180 degrees.

Outlines

00:00

📐 Introduction to Lines and Angles

This paragraph introduces the concepts of parallel and perpendicular lines, defining parallel lines as non-intersecting with the same slope, and perpendicular lines as intersecting at a right angle (90°). It explains how to find the slope of a line perpendicular to a given line and introduces the terms transversal, interior angles, and exterior angles. The concept of alternate interior angles being congruent is also discussed, as well as the properties of corresponding and consecutive angles.

05:01

📐 Complementary and Supplementary Angles

The second paragraph delves into complementary and supplementary angles, explaining that complementary angles add up to 90° while supplementary angles add up to 180°. It provides examples of how to calculate the measures of unknown angles using these properties. The paragraph also introduces the concepts of vertical angles and their congruence, as well as the sum of interior angles for triangles and quadrilaterals.

10:01

📐 Solving Problems with Angles

This paragraph focuses on solving problems involving vertical and corresponding angles, using the properties of congruence and supplementary angles to find unknown angle measures. It provides a series of examples that demonstrate how to apply these concepts to various geometric configurations, emphasizing the use of algebraic expressions and equations to calculate the values of angles.

15:10

📐 Advanced Angle Problems

The fourth paragraph presents more complex angle problems, involving multiple parallel lines and transversals. It explains how to find the measures of angles using the relationships between alternate interior, exterior, and consecutive angles. The paragraph also covers the properties of complimentary and supplementary angles in the context of right and straight lines, and how to use these properties to solve for unknown angles.

20:12

📐 Word Problems and Angle Calculations

This paragraph shifts focus to word problems involving complimentary and supplementary angles. It provides a series of word problems that require the application of the concepts learned in the previous paragraphs to find the measures of unknown angles. The paragraph emphasizes the importance of understanding the relationships between angles and using algebraic methods to solve for their values.

25:14

📐 Final Angle Problems and Summary

The final paragraph presents a few more angle problems involving parallel lines and transversals, focusing on the relationships between various types of angles. It concludes with a summary of the key concepts covered in the video, including parallel and perpendicular lines, transversals, corresponding angles, alternate interior and exterior angles, consecutive interior angles, and the properties of complimentary and supplementary angles.

Mindmap

Keywords

💡Parallel Lines

Parallel lines are two lines in the same plane that do not intersect or meet, no matter how far they are extended. In the video, it is mentioned that parallel lines share the same slope, which means they are永远不会相交的线条。For example, line A is parallel to line B (a∥b), indicating they will never cross each other.

💡Perpendicular Lines

Perpendicular lines are two lines that intersect each other at a right angle, which is 90 degrees. The video emphasizes that when two lines are perpendicular, they meet at a 90° angle, forming what is known as a right angle.

💡Transversal

A transversal is a line that intersects two or more other lines at different points. In the context of the video, a transversal is used to form angles with two parallel lines, which allows for the study of corresponding, alternate, and other types of angles formed by the intersection.

💡Corresponding Angles

Corresponding angles are angles that occupy the same relative position on two parallel lines when intersected by a transversal. They are congruent, meaning they have the same measure. The video script explains that corresponding angles are formed when a transversal crosses two parallel lines, and they are equal in size.

💡Alternate Interior Angles

Alternate interior angles are the angles that are on opposite sides of the transversal and between the two parallel lines. They are congruent because they are created when a transversal crosses two parallel lines and are on the inside or 'alternate' sides of the transversal.

💡Exterior Angles

Exterior angles are the angles that are formed on the outside of the parallel lines when intersected by a transversal. They are also known as 'exterior' because they are outside the parallel lines. The video explains that exterior angles are equal to the sum of the interior angles on the opposite side of the transversal.

💡Consecutive Interior Angles

Consecutive interior angles are the angles that are on the same side of the transversal and within the parallel lines, one after the other. They are supplementary, meaning they add up to 180 degrees. The video script uses this concept to explain the relationship between angles 4 and 6 (∠4 + ∠6 = 180°).

💡Vertical Angles

Vertical angles are the angles opposite each other when two lines intersect. They are always congruent, meaning they have the same measure. The term 'vertical' comes from the fact that these angles are formed when two lines intersect, creating an angle that appears to 'stand upright'.

💡Complementary Angles

Complementary angles are two angles whose measures add up to 90 degrees. They are called 'complementary' because they complete each other to form a right angle. The video script explains that if you have two angles that add up to 90 degrees, they are complementary.

💡Supplementary Angles

Supplementary angles are two angles whose measures add up to 180 degrees. They are called 'supplementary' because they complete each other to form a straight line. The video script explains that if two angles add up to 180 degrees, they are supplementary.

💡Slope

The slope of a line is a measure of its steepness or the rate at which it rises or falls. It is calculated as the change in the vertical direction (y) divided by the change in the horizontal direction (x), often written as 'rise over run'. In the context of the video, the slope is used to determine the parallelism and perpendicularity of lines.

Highlights

Parallel lines are defined as lines that do not intersect.

Parallel lines share the same slope.

Perpendicular lines intersect to form a right angle (90°).

The slope of a line perpendicular to one with a slope of 3/4 is 4/3.

A transversal line intersects two parallel lines, creating interior and exterior angles.

Alternate interior angles are congruent and are on opposite sides of the transversal.

Corresponding angles are congruent and are in the same position on each parallel line.

Consecutive interior angles add up to 180° and are supplementary.

Vertical angles are congruent when two lines intersect.

Complementary angles add up to 90°.

Supplementary angles add up to 180°.

The sum of interior angles of a triangle is 180°.

The sum of interior angles of a quadrilateral is 360°.

The general formula for the sum of interior angles of an n-sided polygon is (n - 2) * 180°.

Word problems involving angles can be solved by setting up equations based on their relationships.

The concept of vertical angles is used to solve for unknown angles in intersecting lines.

Understanding the properties of parallel and perpendicular lines is crucial for solving geometric problems.

Transcripts

Browse More Related Video

Parallel & Perpendicular Lines, Alternate Interior & Exterior Angles, Transversals

Types of Angles and Angle Relationships

Parallel, Intersecting, and Perpendicular Lines | Geometry | Math with Mr. J

Graphing Parallel and Perpendicular Lines

Parallel Lines and Perpendicular Lines - Nerdstudy

Ch. 1.10 Lines

Related Tags

Geometry Basics Parallel Lines Perpendicular Lines Transversals Angles Types Math Tutorial Educational Content Problem Solving Mathematics Education Video Lesson