Work/energy problem with friction | Work and energy | Physics | Khan Academy
TLDRIn this educational video, the presenter tackles a physics problem involving the conservation of energy with a twist: friction. Using a real-world scenario of a 90 kg bike and rider descending a 500-meter long hill with a 5-degree incline, the video demonstrates how to calculate the biker's speed at the bottom. The problem incorporates non-conservative forces, showing that not all potential energy is converted to kinetic energy due to energy loss from friction, which is visualized as heat. The detailed calculation leads to a final velocity of 13.7 meters per second, offering viewers a deeper understanding of energy conservation and friction's role.
Takeaways
- 📚 The problem involves a 90 kg bike and rider starting from rest at the top of a 500-meter long hill with a 5-degree incline.
- 🚵♂️ The biker has potential energy at the start, with no kinetic energy since they are stationary.
- 📈 The initial potential energy is calculated using the formula: mass × gravity × height, which equals 38,455 joules.
- 🌟 The height of the hill is determined using trigonometry: 500 meters (hypotenuse) × sin(5°) ≈ 43.6 meters.
- 🔧 Friction is introduced as a non-conservative force that reduces the total mechanical energy of the system.
- 🚫 The average friction force acting against the biker's motion is 60 newtons.
- 🔄 The work done by friction is negative, as it acts in the opposite direction of the biker's movement.
- 🔋 The final energy at the bottom of the hill is the initial energy minus the work done by friction, which is 8,455 joules.
- 🏎️ The final velocity of the biker is calculated using the kinetic energy formula, resulting in 13.7 meters per second.
- 🌡️ The energy lost to friction is converted into heat, which could be felt as warmth on the bike or rider.
- 💡 The problem demonstrates the concept of energy conservation with the inclusion of non-conservative forces like friction.
Q & A
What is the main topic of the video?
-The main topic of the video is the conservation of energy in a physics problem involving a bike and rider going down a hill with the presence of friction.
What is the mass of the bike and rider combined?
-The combined mass of the bike and rider is 90 kilograms.
What is the length of the hill that the bike and rider are descending?
-The hill is 500 meters long.
What is the average friction force acting against the bike and rider?
-The average friction force is 60 newtons.
How is the hill represented in the problem?
-The hill is represented as a 5-degree incline, or a wedge-like shape, which can be analyzed using trigonometry.
What is the initial form of energy the bike and rider have at the top of the hill?
-The initial form of energy is potential energy, which is calculated as mass times the acceleration due to gravity times height.
How is the height of the hill calculated using trigonometry?
-The height is calculated by using the sine of the incline angle (5 degrees) as the ratio of the opposite side (height) to the hypotenuse (500 meters). The sine of 5 degrees is approximately 0.087, so the height is 500 * 0.087, which equals 43.6 meters.
What is the initial potential energy of the bike and rider?
-The initial potential energy is calculated as 90 kg * 9.8 m/s^2 * 43.6 m, which equals approximately 38,455 joules.
How is the work done by friction represented?
-The work done by friction is represented as negative work because it acts in the opposite direction of the motion. It is calculated as the friction force (60 N) times the distance (500 m), which equals -30,000 joules.
What is the final energy of the bike and rider after descending the hill?
-The final energy is the initial potential energy minus the work done by friction, which is 38,455 J - 30,000 J, equaling 8,455 joules.
What is the speed of the biker at the bottom of the hill?
-The final speed of the biker is calculated by converting the remaining energy into kinetic energy, resulting in a speed of approximately 13.7 meters per second.
What happens to the energy lost to friction?
-The energy lost to friction is not destroyed; it is converted into heat due to the non-conservative nature of frictional forces.
Outlines
🚴♂️ Introduction to Energy Conservation with Friction
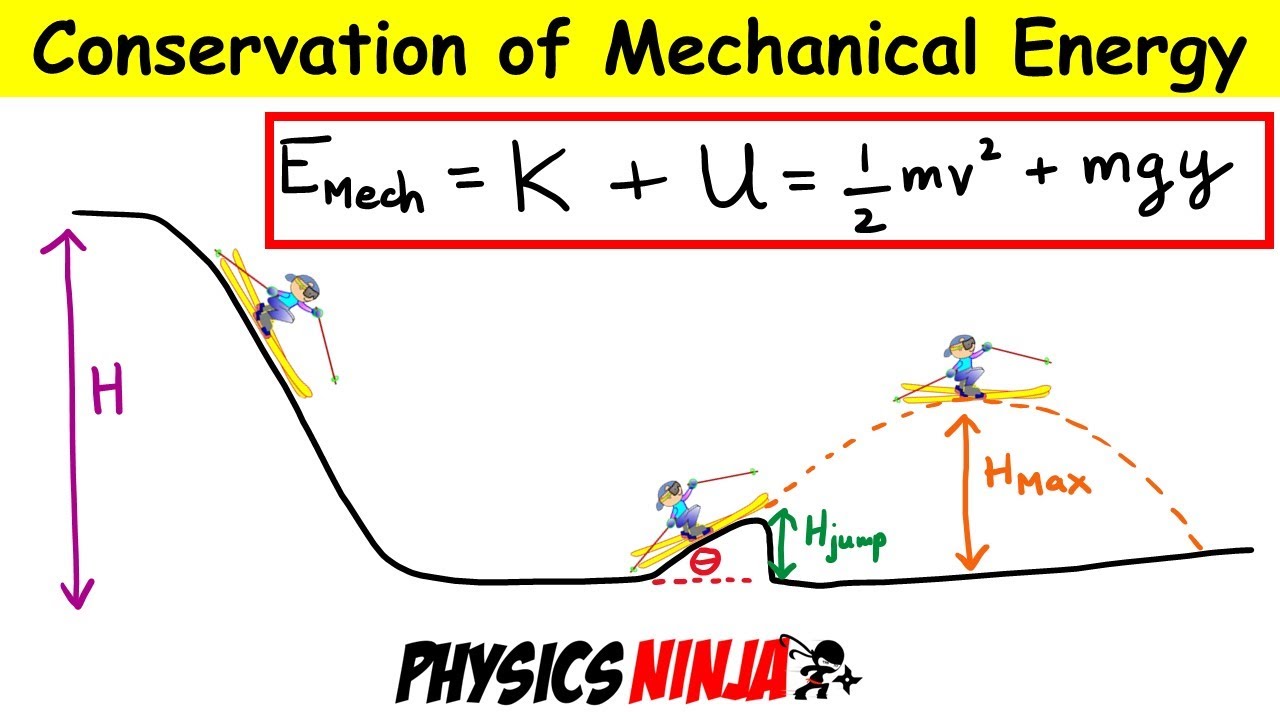
This paragraph introduces a physics problem involving energy conservation with an added twist of friction. The scenario involves a 90 kg bike and rider starting from rest at the top of a 500-meter long hill with a 5-degree incline. The problem aims to find the speed of the biker at the bottom of the hill, considering an average friction force of 60 newtons. The initial energy of the system is potential energy, calculated using mass, gravity, and the height of the hill, which is determined using trigonometry. The paragraph sets up the problem and explains the concept of conservative and nonconservative forces, with friction being a nonconservative force that causes energy loss.
🔧 Calculating Energy Loss Due to Friction
In this paragraph, the focus is on calculating the energy loss due to friction and determining the biker's final speed at the bottom of the hill. The initial potential energy is quantified, and the work done against friction is calculated by multiplying the friction force by the distance traveled. The final energy, which is entirely kinetic energy at the bottom of the hill, is found by subtracting the energy lost to friction from the initial potential energy. Using the kinetic energy formula, the final velocity of the biker is calculated to be 13.7 meters per second. The paragraph emphasizes the concept that friction converts some of the mechanical energy into heat, explaining why energy is not completely conserved in this scenario.
Mindmap
Keywords
💡Conservation of Energy
💡Conservative Forces
💡Friction
💡Potential Energy
💡Kinetic Energy
💡Mechanical Energy
💡Trigonometry
💡Work
💡Incline
💡Acceleration due to Gravity
💡Final Velocity
Highlights
Introduction to a conservation of energy problem with an additional twist of friction.
The problem is sourced from the University of Oregon's physics problem set.
A 90 kg bike and rider start from rest at the top of a 500-meter long hill with a 5-degree incline.
The average friction force acting against the bike and rider is 60 newtons.
The potential energy of the system at the start is calculated using mass, gravity, and height.
The height of the hill is determined using trigonometry, with the sine of the incline angle.
The initial potential energy is calculated to be approximately 38,455 joules.
Friction is introduced as a non-conservative force that reduces the total mechanical energy of the system.
The negative work done by friction is calculated based on the force and distance.
The final energy of the system, after friction, is the kinetic energy of the bike and rider at the bottom of the hill.
The kinetic energy formula is used to find the speed of the biker at the bottom of the hill.
The final velocity of the biker is calculated to be 13.7 meters per second.
Energy lost to friction is transformed into heat, which is a practical application of the concept.
The problem demonstrates the impact of non-conservative forces on the conservation of mechanical energy.
The problem allows for understanding the balance between potential and kinetic energy in the presence of friction.
The example illustrates how to solve physics problems involving both conservative and non-conservative forces.
The problem highlights the practical implications of friction in real-world scenarios, such as biking down a hill.
The video concludes by reinforcing the concept of energy conservation with the inclusion of friction.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: