Intro to springs and Hooke's law | Work and energy | Physics | Khan Academy

Khan Academy
15 Apr 200810:05
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the principles of springs, specifically Hooke's Law, which states that the force needed to compress or elongate a spring is directly proportional to the displacement. The demonstration uses a visual example of a spring on the floor, showing how applying different forces (5 Newtons and 10 Newtons) results in a linear compression. The spring constant, denoted as K, is determined through experimentation, and the law's formula is explained as the restorative force being equal to -K times displacement. The concept is further clarified with an additional problem involving a 2 Newton force and a 1-meter displacement, leading to the conclusion that a 4 Newton force would be needed for a 2-meter displacement.

Takeaways
  • 🌟 Springs naturally rest at a certain position without any force acting on them.
  • 📏 Applying a force of 5 Newtons compresses the spring by a distance of 10 meters in the example given.
  • 🔗 The relationship between the force applied to a spring and its compression or elongation is linear, as described by Hooke's Law.
  • ⚖️ Hooke's Law states that the restoring force of a spring is proportional to its displacement, expressed as F = -kx, where k is the spring constant and x is the displacement.
  • 🔄 The restoring force always acts in the opposite direction of the displacement.
  • 🧪 Experimentation is suggested as a way to understand the linear relationship between force and spring displacement.
  • 🏗️ The spring constant (k) can be determined by applying a known force and measuring the resulting displacement.
  • 📐 When a 10-Newton force is applied, the spring's displacement is twice that of a 5-Newton force (20 units).
  • 🔄 If the spring is stretched with a force of 2 Newtons by 1 meter, the spring constant (k) is calculated to be -2.
  • 🔢 To find the force required to stretch or compress the spring by a certain distance, use the formula derived from Hooke's Law (F = kx).
  • 📹 The video script serves as an educational explanation of the principles of springs and Hooke's Law.
Q & A

  • What is the natural state of a spring?

    -The natural state of a spring is when it is not subjected to any external force, and it rests in its equilibrium position along the floor.

  • What happens to a spring when a force is applied to it?

    -When a force is applied to a spring, it either compresses or elongates depending on the direction of the force, altering its shape from its natural state.

  • How does the spring's behavior relate to the force applied to it?

    -According to Hooke's Law, the force exerted by a spring is linearly proportional to the displacement from its natural state, meaning the more force applied, the greater the compression or elongation.

  • What is Hooke's Law and how is it represented mathematically?

    -Hooke's Law states that the restoring force of a spring is equal and opposite to the product of the spring constant (K) and the displacement (x). Mathematically, it is represented as F = -Kx, where F is the restoring force, K is the spring constant, and x is the displacement.

  • What is the significance of the negative sign in Hooke's Law?

    -The negative sign in Hooke's Law indicates that the restoring force always acts in the opposite direction of the displacement, whether the spring is compressed or stretched.

  • How can you determine the spring constant (K) from the given force and displacement?

    -You can determine the spring constant (K) by rearranging Hooke's Law equation to K = -F/x, where F is the force applied and x is the resulting displacement of the spring.

  • What happens if a spring is compressed or stretched beyond its reasonable tolerance?

    -If a spring is compressed or stretched beyond its reasonable tolerance, it may not return to its original shape, indicating a non-linear behavior or permanent deformation.

  • What is the relationship between the force applied and the distance a spring compresses?

    -The relationship between the force applied and the distance a spring compresses is linear, as described by Hooke's Law. Doubling the force applied would double the compression distance, assuming the spring behaves elastically within its limits.

  • How does the spring constant (K) change if the material or characteristics of the spring change?

    -The spring constant (K) is a measure of the spring's stiffness and depends on factors such as the material, length, wire diameter, and coil spacing. Changing the material or any of these characteristics will result in a different value of K, affecting the spring's behavior under force.

  • What is the role of the spring constant (K) in Hooke's Law?

    -The spring constant (K) in Hooke's Law quantifies the stiffness of the spring. A higher K value indicates a stiffer spring that requires more force to achieve the same displacement compared to a spring with a lower K value.

  • How can you predict the restorative force of a spring given its spring constant and the amount of displacement?

    -To predict the restorative force of a spring, you can use Hooke's Law, F = -Kx. By knowing the spring constant (K) and the displacement (x), you can calculate the magnitude and direction of the restorative force that the spring will exert.

Outlines
00:00
🌟 Introduction to Springs and Basic Concepts

This paragraph introduces the concept of springs and their behavior under force. It begins with a visual representation of a spring at rest against a wall, followed by an explanation of what happens when a force of 5 Newtons is applied, causing the spring to compress. The segment discusses the linear relationship between the force applied and the compression or elongation of the spring, leading to the concept of Hooke's Law. It explains that the spring's restoring force is proportional to its displacement and that this relationship is valid within a spring's elastic limit.

05:01
📐 Hooke's Law and Restoring Force

The second paragraph delves deeper into Hooke's Law, using a mathematical approach to explain the relationship between the force applied to a spring and its displacement. It describes an experiment where a 10-Newton force is applied to see the resulting compression and uses this to derive the spring constant (K). The paragraph clarifies that the restoring force is always opposite in direction to the displacement and is directly proportional to it. It also touches on the concept of spring's elastic limit and how exceeding this limit can result in permanent deformation.

10:02
🔍 Further Examples and Conclusion

The final paragraph provides additional examples to reinforce the understanding of Hooke's Law. It presents a scenario where a spring is stretched by 1 meter under a 2-Newton force and uses this to calculate the spring constant. The paragraph then applies this constant to determine the force required to stretch the spring by 2 meters. The video concludes with a brief mention of the next video, indicating a continuation of the topic.

Mindmap
Keywords
💡Spring
A spring is a mechanical device that can compress or elongate in response to an applied force and then return to its original shape when the force is removed. In the script, the spring serves as the primary subject to explore the concepts of force, displacement, and Hooke's Law. The narrative begins with a visualization of a spring at rest and then examines its behavior under forces of 5 Newtons and 10 Newtons, demonstrating how it compresses differently under these forces.
💡Force
Force, measured in Newtons, is a vector quantity representing an interaction that changes the motion of an object. The script discusses applying forces of 5 Newtons and 10 Newtons to a spring, causing it to compress. This application illustrates the principle that the deformation of a spring is directly related to the magnitude of the applied force.
💡Compression
Compression is the reduction in volume (compressing) of an object due to an applied force. In the video script, compression occurs when forces are applied to the spring, making it shorter and demonstrating how springs can store energy through deformation.
💡Displacement
Displacement in this context refers to the change in position of the spring's end from its original, rest position due to an applied force. The script uses displacement to describe how far the spring compresses or elongates, notably mentioning displacements of 10 meters and 20 meters under varying forces, illustrating the linear relationship between force and displacement as per Hooke's Law.
💡Hooke's Law
Hooke's Law is a principle of physics that states the force needed to extend or compress a spring by some distance is proportional to that distance. The script elaborates on Hooke's Law by showing that a spring's compression is linearly related to the applied force, leading to calculations involving the spring constant (K) and displacement (X) to determine the restorative force.
💡Restorative Force
The restorative force, also known as the restoring force, is the force exerted by a spring to return to its equilibrium state. The script discusses this concept in detail, explaining how a 5 Newton force applied to a spring generates a restorative force that opposes the deformation, thereby keeping the spring in balance.
💡Spring Constant (K)
The spring constant (K) is a value that describes the stiffness of a spring. It's a central part of Hooke's Law, symbolizing the ratio of the force affecting the spring to the displacement caused by it. The script uses this concept to calculate the spring's response to applied forces, revealing the spring's behavior under compression.
💡Equilibrium
Equilibrium refers to a state where all forces acting on an object are balanced, resulting in no net force and, consequently, no acceleration. The script touches on this when discussing how the restorative force of the spring balances out the applied force, keeping the spring in a state of equilibrium.
💡Vector
A vector is a quantity having both magnitude and direction, often used in physics to represent forces. The script differentiates between positive and negative vectors to describe forces and displacements, indicating directions to the left or right from the spring's rest position.
💡Proportional
Proportional relationship indicates that two quantities vary in such a way that if one quantity doubles, the other does as well. The script highlights the proportional relationship between force and displacement in the context of Hooke's Law, demonstrating how the spring's compression is directly proportional to the applied force.
Highlights

The introduction to springs and their basic principles.

The natural state of a spring and its representation.

The effect of a 5 Newton force on the spring and its compression.

The concept of spring compression and elongation with applied forces.

The linear relationship between force applied and spring compression.

The demonstration of Hooke's Law through experimentation.

The formula for the restoring force of a spring: F = -kx.

The calculation of spring constant K using a 5 Newton force.

The application of a 10 Newton force and the resulting spring compression.

The explanation of the restorative force and its direction.

The concept of spring displacement and its calculation.

The real-world application of springs in everyday items like beds and sofas.

The discussion on the limits of spring elasticity and its tolerance.

The calculation of the restorative force when applying different forces.

The explanation of Hooke's Law and its significance in physics.

The demonstration of Hooke's Law with a spring stretched by 2 Newtons.

The calculation of the spring constant K when the spring is stretched by 1 meter.

Transcripts

Browse More Related Video

Potential energy stored in a spring | Work and energy | Physics | Khan Academy

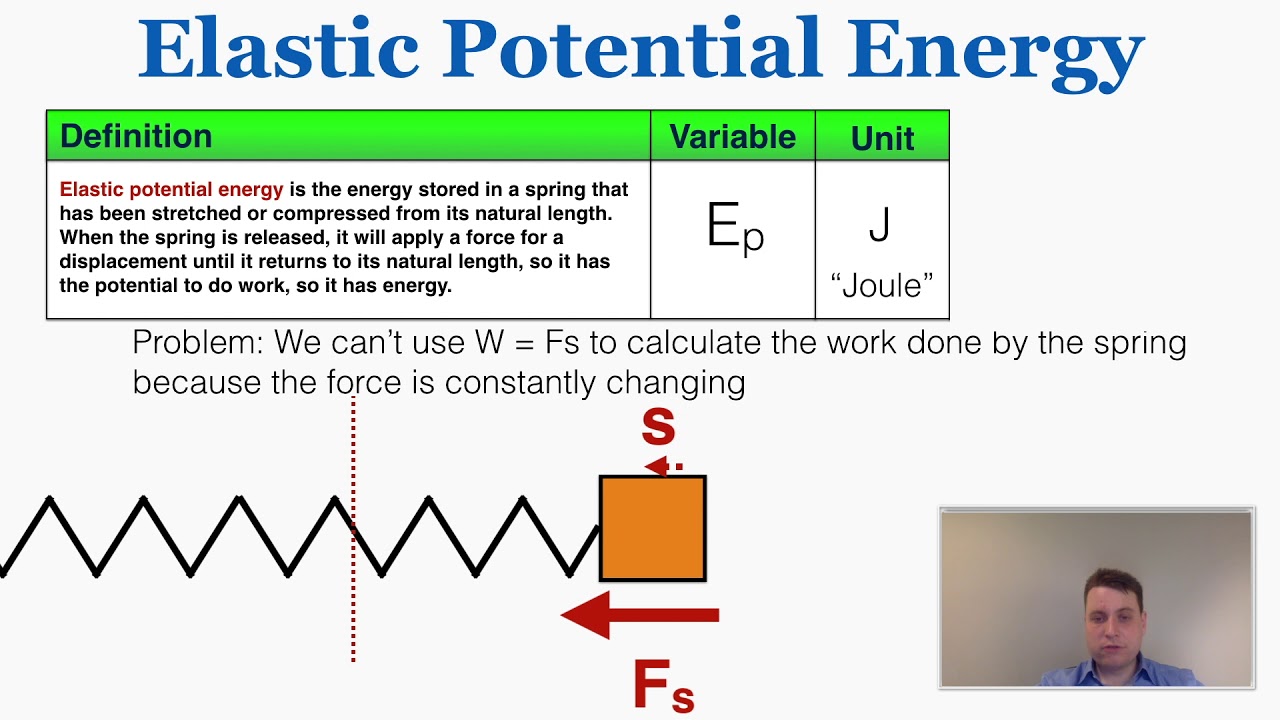
Elastic Potential Energy - IB Physics

Hooke's Law and Elastic Potential Energy

(previous version) Introduction to Elastic Potential Energy with Examples

GCSE Physics - Elastic Potential Energy and F = ke Equations #45

High School Physics - Springs and Hooke's Law

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Spring MechanicsHooke's LawPhysics EducationForce and DisplacementLinear ProportionalityMechanical SystemsRestorative ForceSpring ConstantEngineering ConceptsInteractive Learning