Work example problems | Work and energy | Physics | Khan Academy
TLDRThe video script explains how to calculate the work done on a 4 kg trashcan by various forces when it slides 10 meters on the ground and when it's lifted vertically 2 meters. It covers the work done by tension, kinetic friction, gravitational, and normal forces, using the work formula (Work = Fd cos θ). The net work is then used to determine the final speed of the trashcan using the work-energy principle. The example illustrates that perpendicular forces do no work and that constant velocity motion implies no change in kinetic energy.
Takeaways
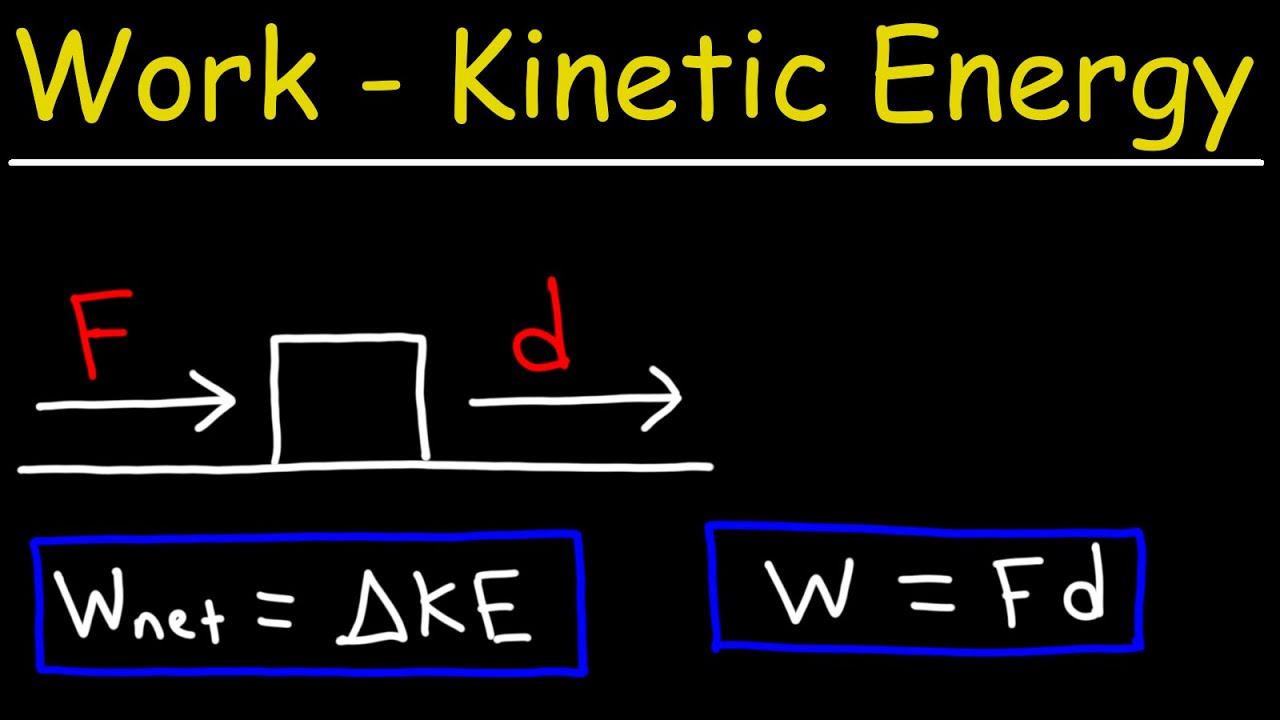
- 🔧 The concept of work in physics is calculated using the formula Work = Fd cos(theta), where F is the force, d is the displacement, and theta is the angle between the force and displacement.
- 🗑️ In the example of the 4 kg trashcan, the work done by the tension force is 500 joules, as the force and displacement are in the same direction (0 degrees).
- 🚫 The work done by friction is -300 joules because it opposes the displacement (180 degrees), resulting in a negative value.
- 📉 Gravitational and normal forces do no work on the trashcan during horizontal motion, as they are perpendicular to the displacement.
- 🌐 The net work done on the trashcan during sliding is 200 joules, which can be found by summing the work done by each individual force.
- 🏃 The work-energy principle states that the net work done on an object equals the change in its kinetic energy, used here to calculate the trashcan's final speed.
- 🔄 When lifting the trashcan vertically with constant velocity, the net work done is 0 joules because the work done by the lifting force is canceled out by the work done against gravity.
- ⏫ The work done in lifting the trashcan 2 meters is 78.4 joules, as the force exerted (equal to its weight) is in the same direction as the displacement.
- 🔄 The gravitational force does -78.4 joules of work during the lift, which is equal and opposite to the work done by the lifting force, leading to no change in kinetic energy.
- 📐 The angle between the force and displacement plays a crucial role in determining if work is done and the sign of that work (positive for same direction, negative for opposite, and zero for perpendicular).
- 📌 Understanding the work done by individual forces and the net work is essential for applying the work-energy principle to solve for changes in an object's kinetic energy.
Q & A
What is the mass of the trashcan mentioned in the example?
-The mass of the trashcan is 4 kilograms.
What force is applied to the trashcan by someone pulling the string?
-A force of 50 newtons is applied to the trashcan.
What is the force of kinetic friction acting on the trashcan as it slides?
-The force of kinetic friction on the trashcan is 30 newtons.
How far does the trashcan slide across the ground?
-The trashcan slides across the ground for a distance of 10 meters.
What is the formula used to calculate work in the context of the problem?
-The formula used to calculate work is Work = Fd cos(theta), where F is the force, d is the displacement, and theta is the angle between the force and the direction of displacement.
Why does the gravitational force not do any work on the trashcan when it slides across the ground?
-The gravitational force does not do any work on the trashcan because the angle between the gravitational force and the direction of displacement is 90 degrees, and the cosine of 90 degrees is 0.
How much work is done by the tension force on the trashcan?
-The work done by the tension force is 500 joules, as the force is in the same direction as the displacement and the angle is 0 degrees, resulting in a cosine value of 1.
What is the net work done on the trashcan as it slides across the ground?
-The net work done on the trashcan is 200 joules, calculated by summing the work done by each individual force.
What principle is used to determine the final speed of the trashcan after it has slid 10 meters?
-The work-energy principle is used to determine the final speed of the trashcan, stating that the net work done on an object is equal to the change in its kinetic energy.
What is the final speed of the trashcan after it has slid 10 meters?
-The final speed of the trashcan is 10 meters per second, calculated using the work-energy principle and the net work done on the trashcan.
How much work is done in lifting the trashcan upwards with a constant velocity for 2 meters?
-The work done in lifting the trashcan upwards is 78.4 joules, calculated using the force of gravity (39.2 newtons), the displacement (2 meters), and the angle of 0 degrees between the force and displacement.
Why is the net work done on the trashcan when it is lifted with constant velocity zero?
-The net work done on the trashcan is zero because the work done by the lifting force (78.4 joules) is exactly negated by the work done by the gravitational force (negative 78.4 joules), as there is no change in kinetic energy during constant velocity motion.
Outlines
🔧 Work Calculation for a Trashcan
The paragraph discusses the concept of work in physics through a practical example of a trashcan being moved. It introduces a 4 kg trashcan and describes the forces acting on it: a 50 N tension force, a 30 N kinetic friction force, gravitational force, and normal force. The work done by each force is calculated using the formula Work = Fd cos(theta), where theta is the angle between the force and the displacement. The net work done on the trashcan as it slides 10 meters is found to be 200 J, which is then used to determine the final speed of the trashcan using the work-energy principle. The paragraph also explores a scenario where the trashcan is lifted vertically for 2 meters, calculating the work done in both scenarios and noting that the net work is zero when moving at a constant velocity, indicating no change in kinetic energy.
Mindmap
Keywords
💡Work
💡Friction
💡Tension
💡Kinetic Energy
💡Displacement
💡Angle (theta)
💡Gravitational Force
💡Normal Force
💡Work-Energy Principle
💡Net Work
💡Cosine
Highlights
The problem involves calculating work done on a 4 kg trashcan.
A 50 N tension force is applied to the trashcan.
The trashcan experiences a 30 N kinetic friction force.
The trashcan slides 10 meters on the ground.
Work is calculated using the formula W = Fd cos(theta).
Tension force does 500 J of work as it's in the same direction as displacement.
Friction force does -300 J of work, opposite to the displacement direction.
Gravitational force does no work as it's perpendicular to displacement.
Normal force also does no work due to its perpendicularity to motion.
Net work done on the trashcan is 200 J.
Using the work-energy principle, the trashcan's final speed is 10 m/s.
Lifting the trashcan with constant velocity requires a 39.2 N force.
Work done in lifting the trashcan is 78.4 J.
Gravitational force does -78.4 J of work when lifting the trashcan.
Net work done during the lifting process is 0 J, indicating constant kinetic energy.
The examples demonstrate the application of work principles in real-world scenarios.
Understanding the relationship between force, displacement, and angle is crucial for work calculations.
Perpendicular forces do not contribute to the work done on an object in motion.
The work-energy principle is a fundamental concept for analyzing changes in kinetic energy.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: