2022 AP Physics 1 Free Response #5

Allen Tsao The STEM Coach
14 May 202213:29
EducationalLearning
32 Likes 10 Comments

TLDRThe script describes a physics experiment involving a spring with an unknown constant, k0, a lightweight hanger, a 5.5 kg object, and a motion detector. The experiment aims to calculate the spring constant by observing the object's oscillation and using the period of the motion. The script also discusses the conservation of energy, comparing kinetic and potential energies at different times, and how these relate to the system's total energy. The experiment is then repeated with a spring of a known constant, 4k0, to determine the new equilibrium position and plot the resulting motion graph.

Takeaways
  • πŸ“ˆ The spring constant (k) is calculated using the formula t/2Ο€ √(m/k), where t is the period of oscillation, m is the mass, and k is the spring constant.
  • πŸ” The period of the oscillation is observed to be 1.25 seconds from the motion detector's output.
  • πŸ€” The mass (m) of the object placed on the hanger is 5.5 kilograms.
  • πŸ“Œ The initial equilibrium position of the hanger is one meter above the motion detector, and the object's weight causes the spring to stretch by 0.4 meters.
  • πŸ“ The spring constant (k) is calculated to be approximately 12.6 N/m based on the given data.
  • πŸ”„ The feature graph indicates that the total kinetic energy of the system is the same at two different times, as shown by the equal slopes of the tangent lines at those points.
  • 🌐 The total potential energy at two different times is the same due to the conservation of energy principle, even though the individual contributions from spring potential energy and gravitational potential energy differ.
  • πŸ”§ The experiment is repeated with a spring constant of 4k0, and the new equilibrium position is determined to be 0.9 meters above the motion detector.
  • πŸ“‰ The new period of oscillation with the increased spring constant is 0.625 seconds, half of the original period.
  • πŸ“ The amplitude of the oscillation remains the same (5 cm or 0.05 meters) despite the change in spring constant.
  • 🎨 The motion of the object after being released from the new equilibrium position is represented by a sketch of a sine curve with adjusted period and amplitude.
Q & A

  • What is the setup of the experiment described in the transcript?

    -The experiment involves a spring of unknown spring constant (k0) attached to the ceiling with a lightweight hanger on the lower end. A motion detector is placed on the floor directly under the hanger. The setup also includes a 5.5 kilogram object placed on the hanger, which is initially at rest in the equilibrium position 1 meter above the motion detector.

  • How is the spring constant calculated in the experiment?

    -The spring constant is calculated using the period of oscillation observed by the motion detector. The period is determined to be 1.25 seconds. Using the formula for the period of a simple harmonic oscillator (T = 2Ο€βˆš(m/k)), where m is the mass (0.5 kg) and T is the period, the spring constant k is calculated by rearranging the formula to solve for k (k = m(T^2)/4Ο€^2) and substituting the known values.

  • What is the significance of the motion detector in this experiment?

    -The motion detector records the height of the bottom of the hanger as a function of time, which provides data on the oscillatory motion of the system. This data is essential for analyzing the system's behavior and for calculating the spring constant.

  • How does the total kinetic energy of the system relate to the graph provided by the motion detector?

    -The total kinetic energy of the system can be inferred from the graph by observing the slopes of the tangent lines at specific points. If the slopes are the same, it indicates that the velocities are the same, and thus the kinetic energies are the same at those points.

  • What happens when the spring constant is changed to 4 times the original value in the experiment?

    -When the spring constant is changed to 4 times the original value, the equilibrium position of the hanging object changes. The new equilibrium position is higher because the spring is stretched less (0.1 meters instead of 0.4 meters), resulting in a new height of 0.9 meters above the motion detector.

  • How does the period of oscillation change when the spring constant is quadrupled?

    -The period of oscillation is inversely proportional to the square root of the spring constant in a simple harmonic motion. When the spring constant is quadrupled, the period becomes half of the original period. Thus, if the original period was 1.25 seconds, the new period would be 0.625 seconds.

  • What is the expected motion of the object after it's released from the equilibrium position in the new setup?

    -The object is expected to oscillate about the new equilibrium position with a period of 0.625 seconds. The motion would still follow a sinusoidal pattern, but the amplitude would remain the same as in the original setup since the same displacement (d0) is given.

  • How can the conservation of energy principle be used to explain the total potential energy at different points in the system's motion?

    -According to the conservation of energy, the total energy in the system remains constant. Therefore, if the kinetic energy is the same at two different times, the total potential energy (spring potential energy plus gravitational potential energy) must also be the same at those times, despite the different heights and stretches of the spring.

  • What is the relationship between the displacement from equilibrium and the total potential energy in the system?

    -The total potential energy of the system is related to the displacement from equilibrium through the spring's potential energy (1/2 kx^2) and the gravitational potential energy (mgh). At two different times where the kinetic energy is the same, the total potential energy must be the same as well, indicating that the sum of the spring's potential energy and the gravitational potential energy is constant at those points.

  • How does the height of the hanger above the motion detector change when the spring constant is increased?

    -When the spring constant is increased, the equilibrium position of the hanger rises. Originally, the hanger was 0.6 meters above the motion detector. With the increased spring constant, the hanger's equilibrium position becomes 0.9 meters above the motion detector, as the spring is stretched less (0.1 meters instead of 0.4 meters).

  • What is the amplitude of the oscillation in the new setup with the increased spring constant?

    -The amplitude of the oscillation remains the same in the new setup, even though the spring constant is increased. This is because the same displacement (d0) from the equilibrium position is given when the object is released, which in this case is 5 centimeters or 0.05 meters.

Outlines
00:00
πŸ“ Calculating Spring Constant from Oscillation Data

The speaker begins by describing a physics experiment involving a spring (k0) with an unknown spring constant, a lightweight hanger, a motion detector, and a 5.5 kg object. The setup involves the object hanging from the spring, which is stretched downward from its equilibrium position and released. The motion detector records the height of the hanger over time, with the output displayed on a graph. The speaker aims to calculate the spring constant using the observed period of oscillation (1.25 seconds) and the mass of the object (0.5 kg). They use the formula for the period of a spring's oscillation (T = 2Ο€βˆš(m/k)) to solve for k, resulting in a calculated spring constant of 12.6 N/m. The speaker also discusses the conservation of energy in the system, particularly focusing on the kinetic energy at two different time points (0.75 and 1.13 seconds) and how the graph's features can indicate equal kinetic energies.

05:01
πŸ”„ Analyzing Energy Conservation in a Spring-Mass System

In this paragraph, the speaker delves deeper into the concept of energy conservation within the spring-mass system. They explain that the total potential energy (due to the spring and gravitational force) and kinetic energy must be the same at two different time points, despite the object being at different heights. The speaker argues that the total energy conservation is the key reason behind this equality. They also discuss the potential energy in terms of displacement from equilibrium and the challenges in making this argument without a detailed analysis. The speaker then describes a repeat of the experiment with a new spring of constant 4k0, where the equilibrium position changes due to the altered spring constant. They calculate the new equilibrium position to be 0.9 meters above the motion sensor, based on the original stretch of the spring and the new spring constant.

10:02
πŸ“ˆ Sketching Motion Graph with Adjusted Spring Constant

The speaker addresses the task of sketching the motion graph for the object after it's released from a new equilibrium position with the modified spring constant (4k0). They note that the period of oscillation will change and calculate the new period to be 0.625 seconds. The speaker then describes the process of plotting the motion graph, considering the amplitude (displacement from equilibrium) and the new period. They provide a step-by-step approach to sketching the graph, including the vertical axis labeling, numerical scale, and grid. Despite acknowledging the complexity of the task, the speaker attempts to estimate the points on the graph and the shape of the sine curve, ultimately expressing some frustration with the calculations involved.

Mindmap
Keywords
πŸ’‘spring constant
The spring constant, denoted as k, is a measure of the stiffness of a spring. It is defined by Hooke's Law as the ratio of the force exerted by the spring to the displacement caused by the force. In the video, the spring constant is initially unknown (k0) and is later doubled to 4k0 for a subsequent experiment. This change in spring constant affects the period of oscillation and the equilibrium position of the system.
πŸ’‘motion detector
A motion detector in the context of the video is a device used to record the height of the bottom of the hanger as a function of time. This data is crucial for analyzing the motion of the object attached to the spring and for determining the spring constant. The motion detector provides a graphical output that can be used to observe the characteristics of the oscillation, such as amplitude and period.
πŸ’‘equilibrium position
The equilibrium position refers to the position where the forces acting on the object are balanced, and there is no net force causing acceleration. In the context of the video, it is the position the object with the spring system settles into when at rest. The equilibrium position changes when the spring constant is altered, as the spring force equals the gravitational force at this point.
πŸ’‘Hooke's Law
Hooke's Law states that the force exerted by a spring is proportional to the displacement from its equilibrium position, which can be expressed as F = -kx. The negative sign indicates that the force direction is opposite to the displacement, aiming to restore the spring to its equilibrium position. This law is fundamental in understanding the behavior of the spring-mass system discussed in the video.
πŸ’‘oscillation
Oscillation refers to the repetitive back-and-forth motion of an object around an equilibrium position. In the video, the object hanging from the spring oscillates up and down due to the restoring force of the spring. The characteristics of this oscillation, such as amplitude and period, are central to the analysis and calculations performed in the video.
πŸ’‘period
The period of an oscillation is the time it takes for one complete cycle of the motion to occur. In the context of the video, the period is used to determine the spring constant and to analyze the system's behavior when the spring constant is changed. The period is a fundamental parameter in the study of oscillations and waves.
πŸ’‘kinetic energy
Kinetic energy is the energy an object possesses due to its motion, given by the formula KE = 0.5 * m * v^2, where m is the mass of the object and v is its velocity. In the video, the kinetic energy of the oscillating object is discussed in relation to the graph's features, indicating that the object has the same kinetic energy at specific times during its oscillation.
πŸ’‘potential energy
Potential energy is the stored energy an object has due to its position in a force field, such as gravitational potential energy (mgh) or elastic potential energy (0.5 * k * x^2). In the video, the potential energy of the spring-mass system is discussed in relation to the conservation of energy and how it changes during the object's oscillation.
πŸ’‘amplitude
Amplitude refers to the maximum displacement of an object from its equilibrium position during oscillation. It is a measure of the extent of the oscillation and is a characteristic of the oscillation's energy. In the video, the amplitude is implicitly considered when discussing the motion of the object and its energy at different points in time.
πŸ’‘displacement
Displacement in the context of the video refers to the change in position of the object from its equilibrium position. It is a vector quantity that can be positive or negative, depending on the direction of the movement relative to the equilibrium position. Displacement is crucial for calculating the potential energy and analyzing the system's energy conservation.
πŸ’‘energy conservation
The principle of energy conservation states that the total energy in an isolated system remains constant, though it may transform from one form to another. In the video, this principle is used to analyze the spring-mass system, where the sum of kinetic and potential energy at any given time is constant, assuming no energy loss due to external factors.
Highlights

A spring of unknown constant k0 is used in an experiment with a lightweight hanger and a motion detector.

The system is set up with the hanger one meter above the motion detector at equilibrium.

A 5.5 kg object is placed on the hanger and the spring is stretched downward from equilibrium before being released.

The motion detector records the height of the hanger as a function of time, providing data for analysis.

The spring constant is calculated using the observed period of oscillation and the mass of the object.

The period of the oscillation is found to be 1.25 seconds.

The mass involved in the experiment is corrected to 0.5 kg, not 5.5 kg.

The calculated spring constant is approximately 12.6 N/m.

The feature graph of the motion detector output indicates the total kinetic energy of the system at specific times.

Kinetic energy is analyzed based on the slopes of the tangent lines at points of interest on the graph.

Total potential energy is discussed in relation to the conservation of energy and the system's displacement from equilibrium.

The experiment is repeated with a spring constant of 4k0, and the new equilibrium position is determined.

The new equilibrium position is calculated to be 0.9 meters above the motion detector.

The period of oscillation changes with the new spring constant, being halved to 0.625 seconds.

The amplitude of the oscillation remains the same despite the change in spring constant.

A sketch of the new motion curve is attempted, considering the new period and amplitude.

The importance of careful calculation and consideration of all variables is emphasized to avoid errors.

Transcripts

Browse More Related Video

AP Physics Workbook 6.I Changing Mass and Period of a Mass Spring SYstem

Energy In a Simple Harmonic Oscillator - Maximum Velocity & Acceleration Calculations

AP Physics Workbook 4.H Potential Energy and Choice of Zero

AP Physics Workbook 2.O Spring Force and Acceleration

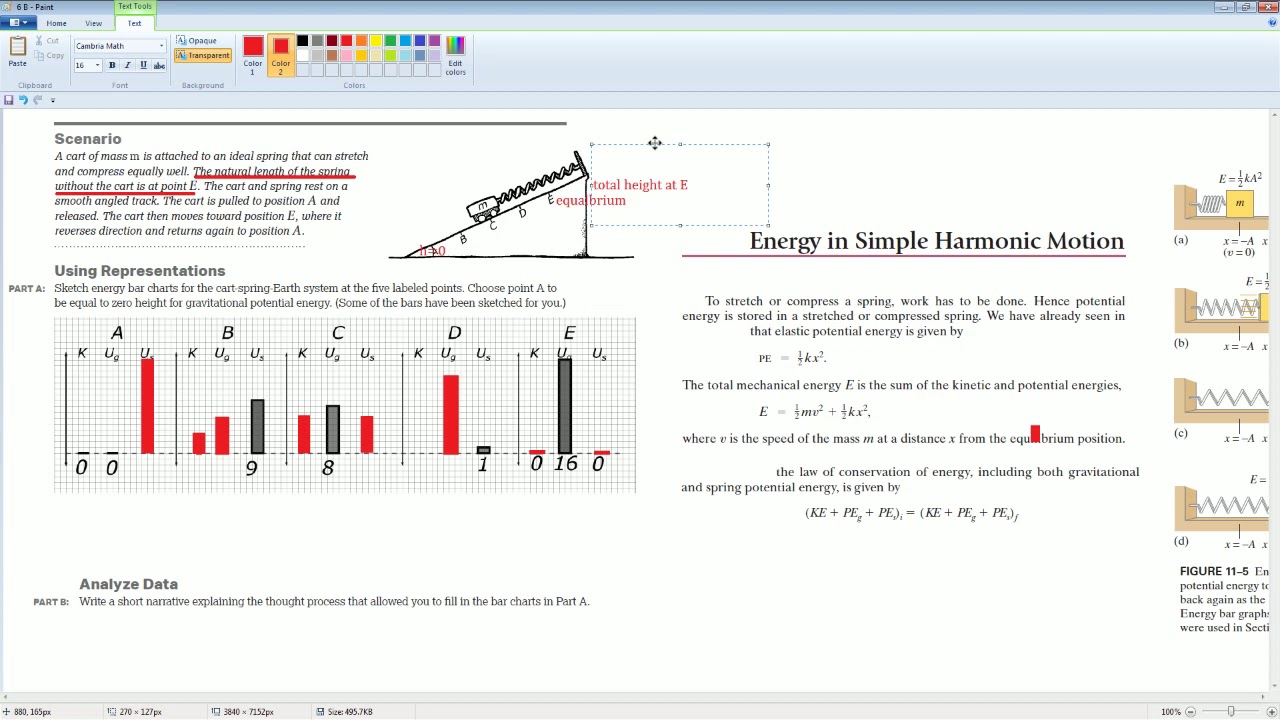
AP Physics Workbook 6.B Simple Harmonic Motion and Energy Review

2 | FRQ (Question 4/5: Short Answer) | Practice Sessions | AP Physics 1

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Spring-Mass OscillationEnergy ConservationPhysics ExperimentSpring Constant CalculationMotion DetectionGraph AnalysisMechanical WavesKinetic EnergyPotential EnergyDynamic Systems