Fractions Made EASY!
TLDRIn this informative video, John, the founder of Tablet Class Math, simplifies the often-dreaded topic of fractions. He introduces two key rules for handling fractions: an easy method for multiplication and division, and a 'bow tie' shortcut for addition and subtraction without the need for finding the lowest common denominator (LCD). John also addresses mixed numbers, emphasizing the importance of practice and understanding of basic fraction concepts for success in mathematics.
Takeaways
- 📚 Fractions can be intimidating, but with the right approach, they become manageable and even easy.
- 🤝 John, the founder of Tablet Class Math and an experienced math teacher, believes every student can succeed in math with clear instruction and practice.
- 🔢 There are two main rules for dealing with fractions: Rule One covers multiplication and division, while Rule Two focuses on addition and subtraction.
- 🗣️ Multiplication and division of fractions are straightforward: multiply or divide the numerators and denominators respectively.
- 🔄 To divide fractions, convert the division problem into a multiplication problem by flipping the denominator to its reciprocal.
- 🎯 When adding or subtracting fractions with the same denominator, simply add or subtract the numerators while keeping the denominator constant.
- 🔑 The Lowest Common Denominator (LCD) is crucial for adding or subtracting fractions with different denominators.
- 💡 The 'Bow Tie Method' is a shortcut for adding or subtracting fractions without having to find the LCD, applicable to both arithmetic and variable fractions.
- 📝 The Bow Tie Method involves multiplying the numerators from the bottom right and bottom left, then the numerators from the top right and top left, and finally combining them over the product of the denominators.
- 📈 Mixed numbers are converted to improper fractions before applying the Bow Tie Method to simplify the process.
- 🚀 Practice is essential for mastering fraction operations, and John offers resources like his pre-algebra course and YouTube channel for further learning.
Q & A
What are the two main rules for dealing with fractions mentioned in the transcript?
-The first rule involves the operations of multiplication and division with fractions, which is considered easy as you simply multiply or divide the numerators and denominators respectively. The second rule focuses on addition and subtraction of fractions, which typically requires finding a common denominator or using the 'bow tie' method as a shortcut.
How does one multiply fractions?
-To multiply fractions, you multiply the numerators together to get the new numerator, and multiply the denominators together to get the new denominator. For example, when multiplying two-thirds by one-fifth, you multiply 2 (the numerator of the first fraction) by 1 (the numerator of the second fraction) to get 2, and then multiply 3 (the denominator of the first fraction) by 5 (the denominator of the second fraction) to get 15. The result is 2/15.
What is the process for dividing fractions?
-Dividing fractions is converted into multiplication by taking the reciprocal of the second fraction (flipping the numerator and denominator) and then multiplying it with the first fraction. For example, to divide 2/3 by 1/5, you flip 1/5 to become 5/1 and then multiply 2/3 by 5/1, resulting in 10/3.
What is the 'bow tie' method mentioned in the transcript and how is it used?
-The 'bow tie' method is a shortcut for adding and subtracting fractions without having to find the lowest common denominator (LCD). You start from the bottom right, multiply the numerators, and place the result in the answer. Then, you go from the bottom left, multiply the denominators, and place that result in the answer as well. This method works for both arithmetic and variable fractions, though the final answer may need to be reduced.
How does the 'bow tie' method change the process of adding fractions with different denominators?
-The 'bow tie' method simplifies the process by allowing you to add fractions with different denominators without finding the LCD. Instead, you multiply the numerators and denominators from the rightmost fraction and then do the same with the leftmost fraction, adding or subtracting the results as necessary.
What are the key points to remember when adding or subtracting fractions with the same denominator?
-If the denominators are the same, you simply add or subtract the numerators and keep the same denominator. The process is straightforward and does not require finding a common denominator or using the 'bow tie' method.
What happens when you need to add or subtract fractions with different denominators?
-When the denominators are different, you must first rewrite the fractions so that they have the same denominator, which is typically the lowest common denominator (LCD). Once the fractions have been rewritten, you can add or subtract the numerators as if they had the same denominator.
How does the transcript suggest dealing with mixed number fractions?
-For mixed number fractions, the transcript suggests rewriting them as improper fractions before applying the multiplication, division, or 'bow tie' methods. This allows for easier computation without the need to separately handle the whole number and fractional parts.
What is the importance of understanding fractions in mathematics?
-Fractions are fundamental to mathematics as they are used in all levels of math, from elementary to advanced topics. Understanding fractions is crucial for success in various mathematical concepts and problem-solving.
What resources does the speaker recommend for further learning and practice with fractions?
-The speaker recommends their pre-algebra course, which includes a chapter on fractions, as well as their YouTube channel, which contains numerous videos covering fractions and other math topics from basic to advanced levels.
How does the transcript address the common struggles students have with fractions?
-The transcript acknowledges that many students find fractions challenging and often avoid them. However, it emphasizes that with clear instruction and practice, all students can become successful in understanding and working with fractions.
Outlines
📚 Introduction to Fractions
The speaker, John, introduces the topic of fractions and acknowledges the common frustrations students face when dealing with them. He offers reassurance that with his guidance, understanding fractions will become easier. John also briefly explains the importance of practice and clear instruction in learning mathematics successfully. He introduces himself as the founder of Tablet Class Math and a middle and high school math teacher with decades of experience.
🧮 Multiplication and Division of Fractions
John explains the process of multiplying and dividing fractions, emphasizing that these operations are relatively straightforward. He details that to multiply fractions, one multiplies the numerators together and the denominators together. For division, fractions are converted into multiplication by taking the reciprocal of the second fraction. John also addresses mixed numbers, explaining how to convert them into improper fractions for easier calculation. He assures viewers that mastering these rules will make dealing with fractions much simpler.
🔢 Adding and Subtracting Fractions
The speaker delves into the more complex aspect of fractions, which is adding and subtracting them. He introduces the concept of the lowest common denominator (LCD) and provides a method for finding equivalent fractions with the same denominator. John then presents a shortcut method, the 'bow tie' method, for adding and subtracting fractions without the need to find the LCD. He demonstrates this method with examples and assures viewers of its accuracy, although sometimes the result may need to be simplified.
🎓 Bow Tie Method for Fractions
John elaborates on the 'bow tie' method for adding and subtracting fractions, emphasizing its simplicity and effectiveness. He provides a step-by-step guide on how to use this method, starting from the bottom right and moving diagonally to the top left, multiplying numerators and denominators in a specific order. He demonstrates the method with a subtraction example and a mixed number example, showing that it can be applied to various fraction problems without needing to find the LCD.
📈 Final Thoughts and Resources
In the conclusion, John reiterates the importance of understanding fractions as they are fundamental to all levels of math. He encourages viewers to practice and offers his pre-algebra course and YouTube channel as resources for further learning. John also invites viewers to subscribe to his channel for a wide range of math content and thanks them for their time, wishing them success in their mathematical endeavors.
Mindmap
Keywords
💡fractions
💡lowest common denominator (LCD)
💡multiplication
💡division
💡addition
💡subtraction
💡mixed numbers
💡reciprocal
💡bow tie method
💡practice
Highlights
The video introduces two main rules for dealing with fractions, which simplifies the process and makes it more approachable for students.
Multiplication and division of fractions are considered one rule, which is straightforward and easy to understand.
To multiply fractions, simply multiply the numerators together and the denominators together.
Division of fractions is converted into multiplication by flipping the second fraction upside down to find its reciprocal.
For addition and subtraction of fractions, the focus is on finding or working with the lowest common denominator (LCD).
When adding or subtracting fractions with the same denominator, you keep the denominator and directly add or subtract the numerators.
A 'bow tie' method is introduced as a shortcut for adding and subtracting fractions without finding the LCD, which can simplify the process.
The bow tie method involves multiplying the bottom right and top left numbers first, then the bottom left and top right, creating a crisscross pattern.
The video emphasizes the importance of practicing fractions and understanding their applications across different levels of math.
Mixed numbers are converted into improper fractions to simplify the process of addition and subtraction.
The bow tie method can also be applied to mixed number fractions, further demonstrating its versatility.
The video offers additional resources for learning about fractions, including a pre-algebra course and a YouTube channel with over a thousand math videos.
The presenter, John, has decades of teaching experience and believes that every student can succeed in math with the right instruction and practice.
The video aims to make students more comfortable with fractions and to provide them with techniques that can help them throughout their mathematical journey.
Transcripts
Browse More Related Video
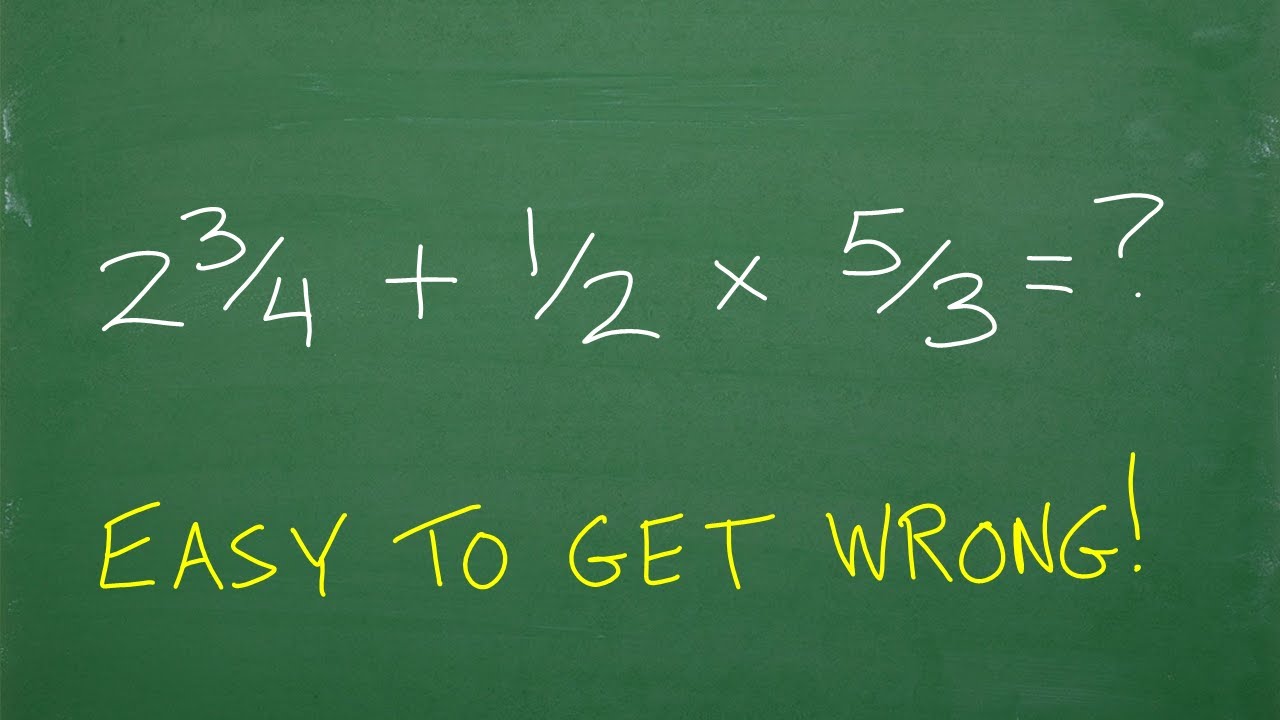
(2 and 3/4) plus 1/2 times 5/3 = ? What’s the first thing you should be thinking in this problem?
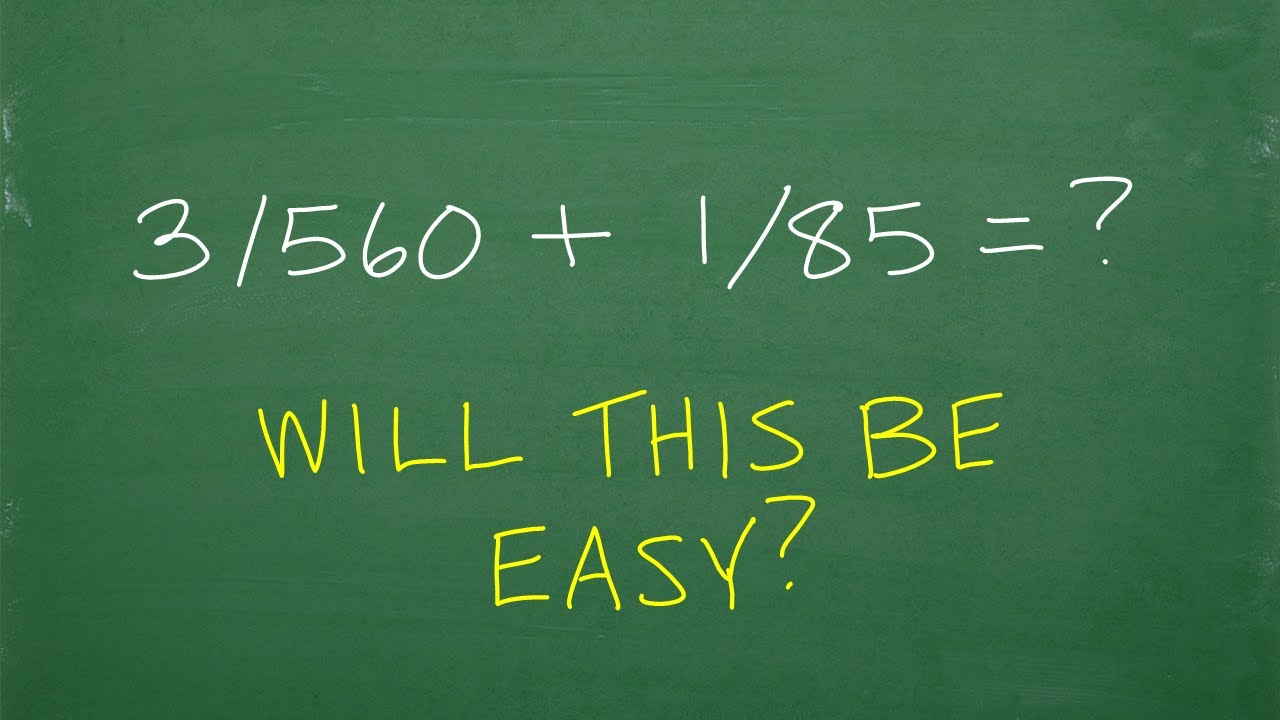
3/560 + 1/85, will this be EASY?
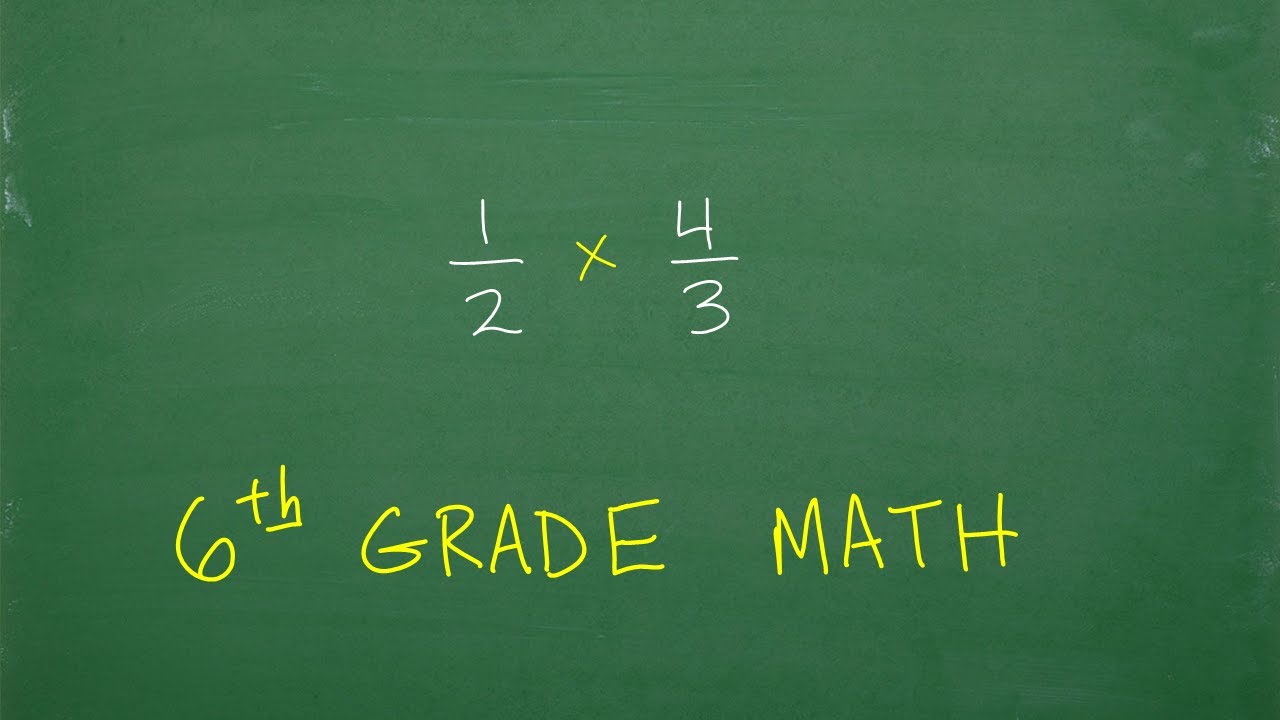
How to Multiply Fractions – 6th Grade Math

How To Use The Order of Operations (PEMDAS) – Example Problem

3/2(x + 4) = 5 – 1/3(4 – x), many don’t know the EASY way to solve!
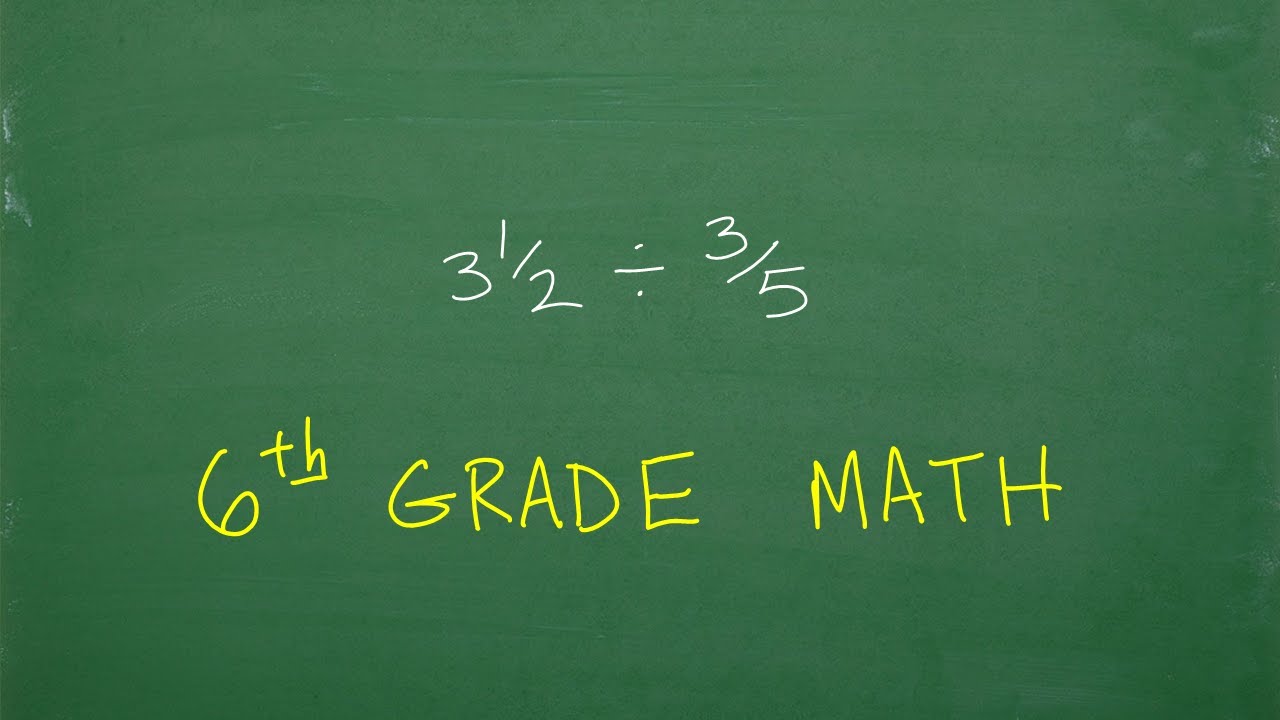
How to Divide Fractions – 6th Grade Math
5.0 / 5 (0 votes)
Thanks for rating: