Work as area under curve | Work and energy | Physics | Khan Academy
TLDRThe video script explores the concept of work done in physics, particularly when pushing a hamburger as an example. It explains that work, defined as the force applied in the direction of motion times the displacement, can be calculated using the work formula or by understanding the geometrical significance of force over distance. The script introduces an alternate method for calculating work, especially useful for varying forces, by considering the area under the force-graph. This is demonstrated through a step-by-step explanation of how the area under a rectangle (for constant force) or a triangle (for varying force) can represent the work done. The concept is further clarified with examples of negative work and varying force, emphasizing the practical application of this approach in solving complex physics problems without calculus.
Takeaways
- 👍 The work done on an object, like pushing a hamburger, can be calculated by multiplying the force applied in the direction of motion by the distance moved.
- 📈 A constant force applied over a distance results in work that can be visualized as the area under a force vs. position graph.
- 💭 An alternative to the standard work formula involves understanding the geometric significance of work through the area under the force graph.
- 🔨 When the force is constant, the area under the force vs. position graph (a rectangle) directly represents the work done.
- 🤔 For varying forces, calculating work becomes more complex as the force applied changes over the distance.
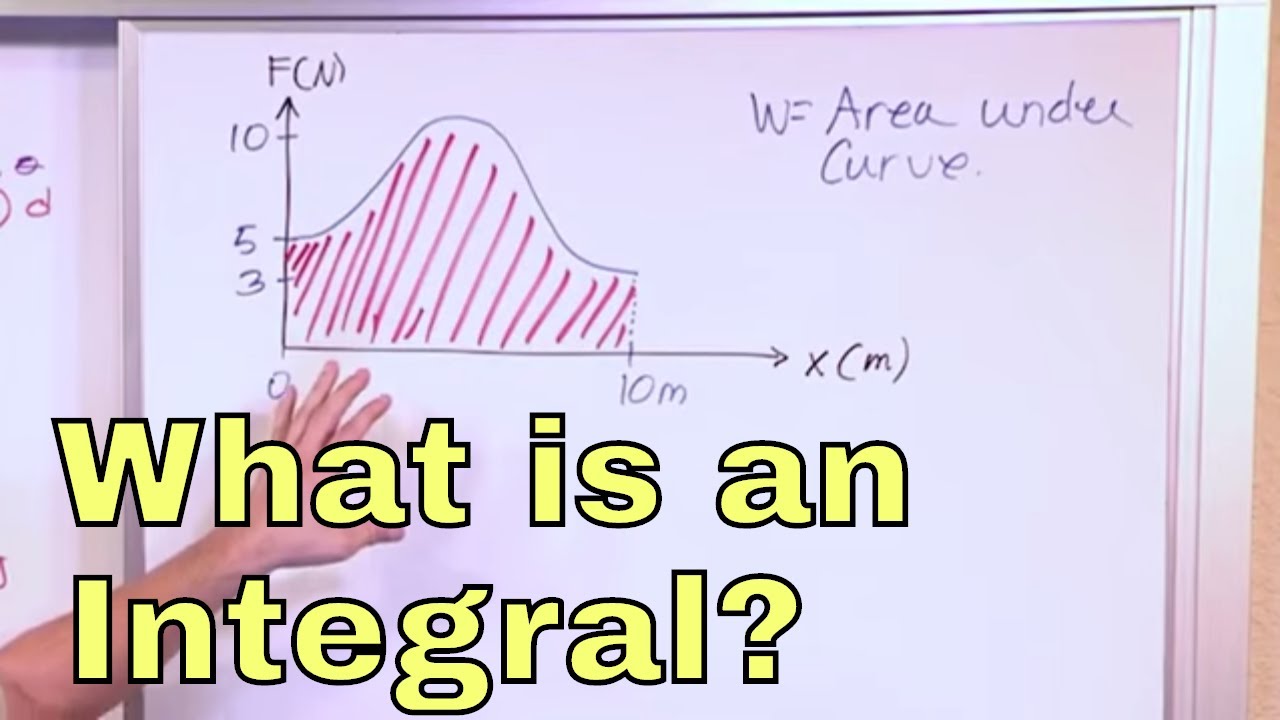
- 👀 Demonstrates that for non-constant forces, the area under the force vs. position graph still equals the work done, using a conceptual approach involving infinitesimally small rectangles.
- 📊 The area under a triangle in a force vs. position graph can represent work done by a force that diminishes to zero over a distance.
- ✅ Highlights the power of this geometric approach to work, enabling the calculation of work done without relying on calculus for varying forces.
- 📃 Explains that the concept of calculating work as the area under the force graph applies universally, not just for constant forces or simple shapes like rectangles and triangles.
- ⚡ Warning that when calculating the total work from a force vs. position graph, one must consider the area between the force line and the x-axis, especially when forces can have negative values.
Q & A
What is the scenario described in the transcript?
-The scenario involves pushing a hamburger to the right with a force of four newtons over a distance of five meters and discussing the concept of work done in this process.
How much work was done in the hamburger example with a constant force?
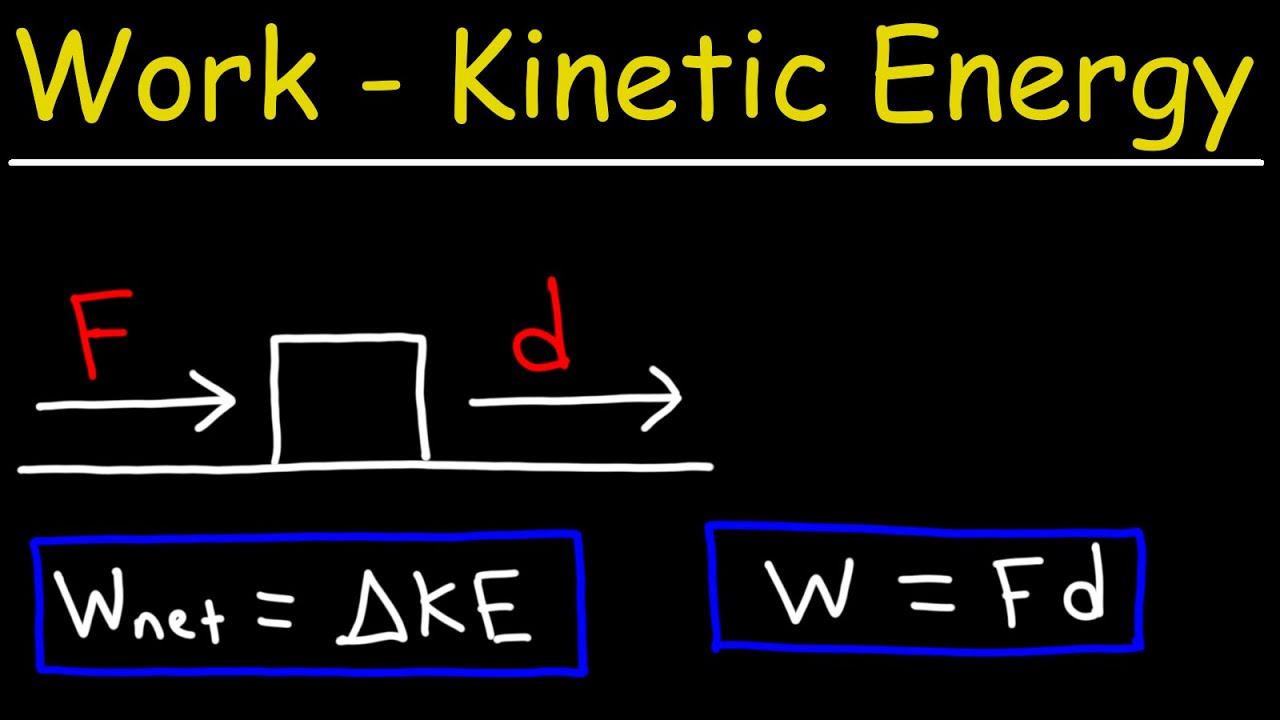
-The work done was 20 joules, calculated as the force (4 newtons) times the displacement (5 meters).
What is the significance of the horizontal line in the force graph?
-The horizontal line signifies that a constant force of four newtons was applied throughout the entire displacement of five meters.
Why is the cosine theta term not needed in this example?
-The cosine theta term is not needed because the force was already in the direction of motion, making the angle zero, and cosine of zero is one, which does not change the value.
What is the alternative method to calculate work when the force is not constant?
-The alternative method is to find the area under the force versus position graph, which represents the work done by the force, even when it is varying.
How does the area under the force graph represent work done?
-The area under the force graph represents the work done because it accounts for the total effect of the force applied over the displacement, considering the varying magnitude of the force if applicable.
What is the process of breaking down the force into infinitesimal rectangles to find the area under a varying force graph?
-The process involves dividing the force into many small constant forces over tiny displacements, calculating the area of each small rectangle (force times displacement), and summing these areas to approximate the total area under the graph, which equals the work done.
How is negative work represented in the context of this problem?
-Negative work is represented when the force is applied in the opposite direction of motion, resulting in a negative area under the force graph, indicating that the force is doing work against the direction of displacement.
What is the formula for work when the force is constant?
-The formula for work when the force is constant is W = Fd cos(theta), where W is work, F is the force, d is the displacement, and theta is the angle between the force and displacement vectors.
How does the shape of the force graph affect the calculation of work?
-The shape of the force graph determines how the area under it is calculated. Different shapes (e.g., rectangles, triangles) require different formulas to find the area, but the principle that the area under the graph equals the work done remains the same.
What is the total work done if the force starts negative and becomes positive, as in the example of pushing to the left then to the right?
-The total work done is the sum of the work done in each segment. For the portion where the force was negative (pushing to the left), the work was -1 joule, and for the portion where the force was positive (pushing to the right), the work was +4 joules, resulting in a total work of +3 joules.
Outlines
🍔 Understanding Work Done with Constant Force
This paragraph introduces a scenario where a hamburger is pushed to the right with a constant force of four newtons over a distance of five meters. The instructor explains that the work done can be calculated using the work formula, but instead, they present an alternative method. This method involves visualizing the force as a horizontal line on a graph and recognizing that the area under this line (which forms a rectangle) represents the work done. The instructor calculates the work as positive 20 joules and emphasizes that when the force is constant, the area under the force graph equals the work done. This concept is further extended to handle more complex situations where the force is not constant.
📈 Calculating Work with Varying Force Using Graphs
In this paragraph, the instructor discusses how to calculate work done when the force is not constant. They propose breaking down the force into infinitesimally small rectangles, each representing a small displacement with a constant force. By summing the areas of these rectangles, the total work done is found, which is equivalent to the area under the force graph. The concept is illustrated with an example of pushing the hamburger with decreasing force, resulting in a triangular force graph. The instructor explains that the area under this triangle can be found using the formula for the area of a triangle, yielding the work done as ten joules. The key takeaway is that the area under any force versus position graph, regardless of the force's constancy, equals the work done, providing a powerful tool for calculating work in various situations without the need for calculus.
🔄 Dealing with Negative Work and Variable Forces
The final paragraph addresses a situation where the force starts negative and becomes positive, representing a change in direction of the force. The instructor explains how to calculate the total work done by considering the area under the force curve from the force line to the x-axis. They clarify that the work done is represented by the finite area under the curve, not an infinite area. The example given involves pushing the hamburger first to the left (negative work) and then to the right (positive work). The areas under the respective force triangles are calculated, with negative work being represented by a negative area. The total work done is the sum of the positive and negative work, resulting in a net work of three joules. The paragraph emphasizes the importance of correctly identifying the area under the graph that corresponds to the work done and highlights the versatility of using force graphs to calculate work regardless of the force's variability.
Mindmap
Keywords
💡work
💡force
💡displacement
💡newtons
💡joules
💡cosine theta
💡area under the graph
💡calculus
💡infinitesimal
💡negative work
💡mechanical processes
Highlights
Exploring the concept of work done in physics, specifically in the context of pushing a hamburger.
Introducing an alternate way to think about work beyond the traditional formula.
Using a geometrical approach to understand work as the area under a force graph.
Demonstrating that work done is equivalent to the area of a rectangle when force is constant.
Explaining that the work formula can be simplified by removing the cosine theta term when the force is in the direction of motion.
Calculating the work done on the hamburger as positive 20 joules using the area under the force graph.
Discussing the application of this concept for varying forces, where calculus might otherwise be necessary.
Describing a method for calculating work done by a varying force by breaking it down into infinitesimal constant forces.
Using the area under a triangle to find the work done when force diminishes over a distance.
Providing a clear explanation of how to handle negative work and the significance of the direction of force.
Clarifying that the total work done is the sum of the work done over discrete segments of the force graph.
Emphasizing that the area under the force graph represents work done, even when the force is not constant.
Explaining that the area under the force graph must be considered from the force line to the x-axis to accurately represent work done.
Illustrating how to find the work done with a changing force by calculating the area of triangles under the graph.
Summarizing the key takeaway that the area under any force versus position graph equals the work done, providing a powerful tool for various scenarios.
Reiterating that for constant forces, the traditional work formula can be used, but for varying forces, the area under the graph is the preferred method.
Concluding with the practical application of determining work done by simply finding the area under a force versus position graph, regardless of the force's constancy.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: