AP Physics Workbook 4.C Energy Graphs
TLDRThe video script discusses the concept of work, energy, and the conservation of mechanical energy in the context of a ball falling from a height H. It explains the relationship between potential energy (U), kinetic energy (K), and the total mechanical energy of the system, emphasizing that these energies are conserved and how they change as the ball falls. The script provides a detailed analysis of the energy graphs versus distance fallen and time, highlighting the linear and quadratic relationships, and explains the energy conversion from potential to kinetic energy at different stages of the fall.
Takeaways
- 📈 The problem involves graphing potential energy (U), kinetic energy (K), and total mechanical energy for a ball falling from rest at a height H, ignoring air resistance.
- 🌐 Potential energy (U) is given by the formula U = mgh, where m is mass, g is the acceleration due to gravity, and h is the height.
- ⚽ Kinetic energy (K) is calculated using K = (1/2)mv^2, with m being mass and v being velocity.
- 📊 The potential energy graph starts at the top and decreases linearly to the bottom as the ball falls.
- 🏃 The kinetic energy graph starts at zero and increases quadratically as the ball accelerates due to gravity.
- 🔄 At the midpoint of the fall (H/2), the potential and kinetic energies are equal, representing a balance in the system's total mechanical energy.
- 🔢 The total mechanical energy of the system remains constant throughout the fall, assuming no energy loss to air resistance.
- 🕒 When graphing energy as a function of time, the potential energy decreases quadratically, while the kinetic energy increases quadratically over time.
- 🎯 At half the fall time (T = √(2gH)/2g), there is more potential energy than kinetic energy, as the ball has not yet reached the midpoint of its fall.
- 📉 The rate of change of energy starts slow and increases over time due to the quadratic nature of the gravitational and kinetic energy equations.
- 📌 The key to solving the problem is understanding the relationship between potential and kinetic energy, and how they convert into each other as the ball falls.
Q & A
What is the scenario described in the transcript?
-The scenario involves a ball released from rest at a height H above the floor, considering the system to be the ball and the Earth, with air resistance being negligible.
What are the three types of energy being graphed in the scenario?
-The three types of energy being graphed are gravitational potential energy (UG), kinetic energy (K), and total mechanical energy for the system.
How is potential energy (UG) calculated in this problem?
-Potential energy (UG) is calculated as mgh, where m is mass, g is the gravitational field strength, and h is the height.
What is the relationship between potential energy and distance fallen in the transcript's explanation?
-The potential energy is linearly related to the distance fallen, represented by mgΔy, where Δy is the distance fallen.
How is kinetic energy (K) described in terms of velocity in the transcript?
-Kinetic energy (K) is described as one-half mv^2, where m is mass and v is velocity.
What is the significance of the point where the ball has fallen half the distance?
-At the point where the ball has fallen half the distance, the total mechanical energy of the system is equally divided between potential and kinetic energy.
How does the total mechanical energy of the system change as the ball falls?
-The total mechanical energy of the system remains constant during the fall, as potential energy is converted into kinetic energy.
What is the relationship between gravitational potential energy and time in the transcript's explanation?
-Gravitational potential energy is quadratically related to time, as described by the equation Δy = (1/2)gt^2, where g is the acceleration due to gravity and t is time.
How does the kinetic energy of the ball change with time?
-The kinetic energy of the ball changes quadratically with time, starting slow and then increasing as time progresses, due to the quadratic nature of the relationship between velocity (v = gt) and time.
At what time is there more potential energy than kinetic energy in the system?
-There is more potential energy than kinetic energy in the system when the time is less than half of the total fall time, as indicated by the quadratic nature of the energy with respect to time.
What is the conclusion drawn from the analysis of the energy graphs?
-The conclusion is that the total mechanical energy of the system remains constant, with the conversion between potential and kinetic energy being directly proportional and maintaining a linear relationship when graphed against distance fallen.
Outlines
📚 Introduction to AP Physics: Work and Energy
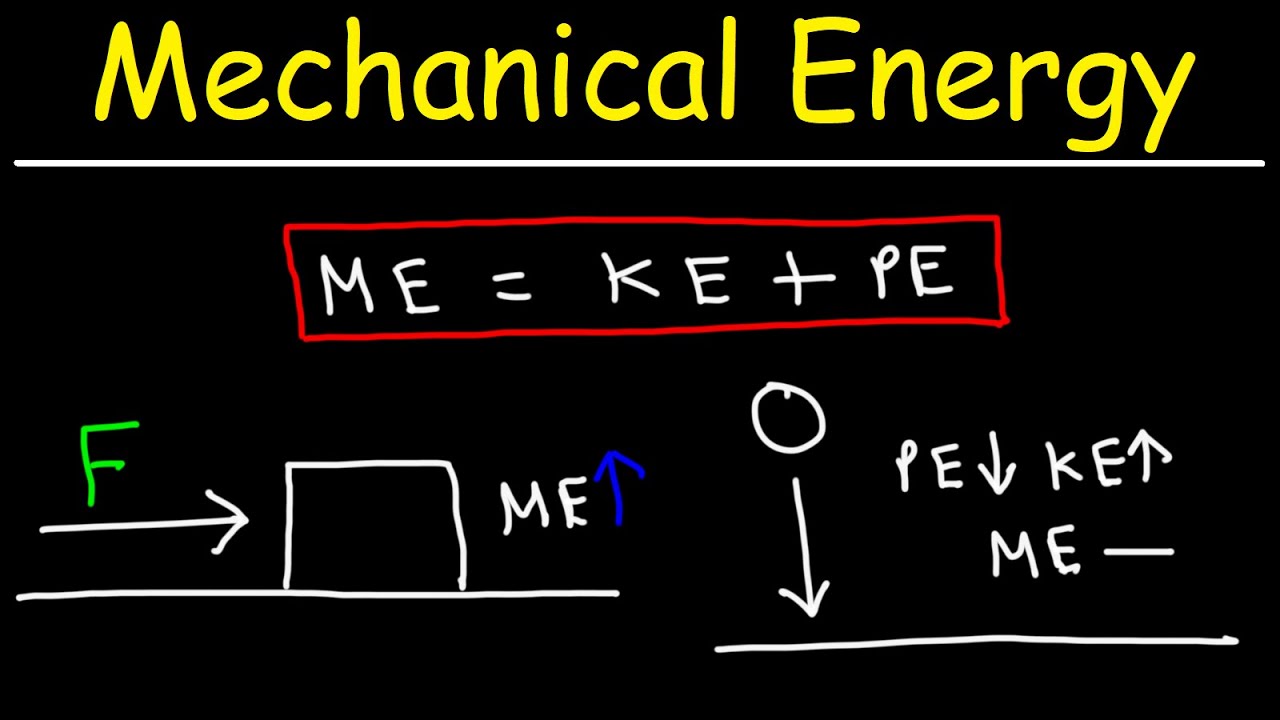
This paragraph introduces the topic of work and energy in the context of AP Physics. It sets the scenario of a ball released from rest at a height H above the floor, considering the system to be the ball and the Earth. It emphasizes the importance of air resistance being negligible. The main task is to graph the potential energy (U) versus the distance fallen (K), as well as kinetic energy versus distance fallen, and the total mechanical energy for the system. The paragraph provides notes on labeling the graphs and introduces the formula for potential energy (PE = mgh) and kinetic energy (KE = 1/2mv^2), highlighting the need for kinematic equations to solve the problem. The discussion includes the visual representation of how gravitational energy decreases and kinetic energy increases linearly as the ball falls, and how the total energy of the system remains constant, resulting in a linear graph for potential and kinetic energy versus distance.
📉 Graphing Energy as a Function of Time
This paragraph delves into graphing energy as a function of time rather than distance. It explains how the potential and kinetic energies are quadratic in nature when plotted against time. The paragraph details the kinematics equations used to derive the quadratic relationship, particularly focusing on the relationship between height (ΔY), gravitational acceleration (g), and time (t). It describes the graph of potential energy decaying quadratically from the start and how kinetic energy builds up gradually due to its quadratic nature. The paragraph also addresses the point at half the distance fallen, explaining the balance of potential and kinetic energy at that point. The summary emphasizes the constant total mechanical energy of the system and how the energy conversion between potential and kinetic is directly proportional, maintaining the system's mechanical energy throughout the fall. The paragraph concludes with an explanation of why at half the time, there is more potential energy than kinetic energy, providing a deeper understanding of the energy dynamics at play.
Mindmap
Keywords
💡Potential Energy
💡Kinetic Energy
💡Mechanical Energy
💡Gravitational Energy
💡Kinematics
💡Conservation of Energy
💡Acceleration Due to Gravity
💡Distance Fallen
💡Linear and Quadratic Relationships
💡Graphs
💡Work
Highlights
The scenario involves a ball released from rest at a height H above the floor, considering the system to be the ball and the earth with air resistance ignored.
The task is to graph the potential energy U_G versus distance falling K, kinetic energy versus distance fallen, and the total mechanical energy versus distance falling for the system.
Labels should be included on the images to clarify the different types of energy being represented.
Potential energy (U_G) is represented by the formula U_G = m*g*H, where m is mass, g is the acceleration due to gravity, and H is the height.
Kinetic energy (K) is given by the formula K = 0.5*m*v^2, with m being mass and v being velocity.
Kinematics are essential for understanding the relationship between potential and kinetic energy as the ball falls.
The total mechanical energy of the system remains constant, as the sum of potential and kinetic energy at any point equals the initial potential energy at the top.
The potential energy graph starts at the top and decreases linearly to the bottom, representing the loss of gravitational potential as the ball falls.
The kinetic energy graph starts at zero and increases quadratically, reflecting the ball's accelerating motion as it falls.
At the midpoint of the fall (H = 0.5*H), the potential and kinetic energies are equal, showing a direct proportionality between them.
When graphed as a function of time, both gravitational and kinetic energies are quadratic in nature, with the kinetic energy starting slow and then increasing over time.
At half the time of the fall, there is more potential energy than kinetic energy, as the ball has not yet reached the halfway point in its descent.
The total mechanical energy graph is a flat line, representing the conservation of mechanical energy throughout the ball's fall.
Understanding the energy conversions and their graphical representations is crucial for solving problems in physics, particularly those involving work and energy.
The kinematics equations are fundamental in relating potential and kinetic energy in terms of distance and time, as demonstrated by the equations used throughout the explanation.
This analysis provides a clear understanding of the conservation of mechanical energy and the relationship between potential and kinetic energy in a falling object scenario.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: