Disk & Washer Method - Calculus
TLDRThis video tutorial explains how to calculate the volume of a solid formed by rotating a region around the x-axis or y-axis using the disc method and washers method. The key concept is to find the cross-sectional area, which becomes a circle when rotated, and then integrate this area over the given interval to find the total volume. The video provides clear examples and step-by-step instructions, making it easy to understand and apply these mathematical techniques.
Takeaways
- 📚 The concept of calculating the volume of a solid by rotating a region around an axis is introduced, specifically the x-axis or y-axis.
- 🔄 Two primary methods for such calculations are discussed: the disc method and the washers method.
- 💿 The disc method involves calculating the volume by considering cross-sectional areas as discs when rotated around the x-axis, forming a cylinder-like shape.
- 📊 The volume of a cylinder is determined by multiplying the cross-sectional area (πr²) by the height (h), leading to the integral ∫πr²h dx when finding volumes.
- 🔄 For rotation around the y-axis, the process is similar, but the cross-sectional area is considered as washers, leading to the integral ∫πr²dy.
- 📈 The radius (r) for the x-axis rotation is determined by the distance from the curve to the x-axis, and for the y-axis rotation, it's the distance to the y-axis.
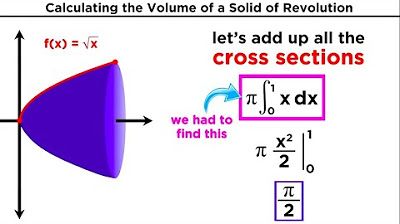
- 📝 Examples are provided to illustrate the process, including the function y = √x rotated around the x-axis from x=0 to x=4, resulting in a volume of 8π cubic units.
- 🌀 The function y = 1/x rotated around the x-axis from x=1 to x=3 is used to demonstrate the disc method, yielding a volume of 2π/3 cubic units.
- 🔄 Another example involves the function y = x² rotated around the y-axis from y=0 to y=4, with the volume calculated using the integral ∫π(√y)² dy, resulting in a volume of 8π cubic units.
- 📊 The final example showcases the function y = x^(2/3) rotated around the y-axis from y=0 to y=1, with the volume calculated using the integral ∫πy^(3/2) dy, leading to a volume of π/4 cubic units.
- 🔑 The key to solving these problems is understanding how to express the radius (r) in terms of the variable associated with the axis of rotation and how to set up and evaluate the appropriate integrals.
Q & A
What is the main topic of the video?
-The main topic of the video is how to calculate the volume of a solid formed by rotating a region around the x-axis or y-axis using the disc method and washers method.
What is the disc method?
-The disc method involves taking the cross-sectional area of a region revolved around an axis, treating it as the radius of a disc, and calculating the volume by integrating the area of these discs over the given interval.
How is the volume of a cylinder calculated?
-The volume of a cylinder is calculated by multiplying the area of the cross-sectional circle (pi * r^2) by the height of the cylinder.
What is the formula for finding the volume of a solid when revolving around the x-axis?
-The formula for finding the volume when revolving around the x-axis is V = pi * ∫[a, b] (r(x)^2) dx, where r(x) is the radius as a function of x.
What is the formula for finding the volume of a solid when revolving around the y-axis?
-The formula for finding the volume when revolving around the y-axis is V = pi * ∫[c, d] (r(y)^2) dy, where r(y) is the radius as a function of y.
How do you find the volume of the solid formed by rotating the curve y = √x from x = 0 to x = 4 around the x-axis?
-The volume is found by integrating the function: V = pi * ∫[0, 4] (√x)^2 dx, which simplifies to V = pi * ∫[0, 4] x dx, and upon evaluating the integral, the result is 8pi.
What is the function y = 1/x rotated around the x-axis bounded by x = 1 and x = 3?
-Rotating the function y = 1/x around the x-axis from x = 1 to x = 3 forms a solid. The volume of this solid is found by the integral V = pi * ∫[1, 3] (1/x)^2 dx, which evaluates to V = 2pi/3.
How do you determine the radius for the washers method?
-In the washers method, the radius is determined by the distance from the axis of rotation to the curve. Depending on the axis of rotation, this could be the distance from the x-axis or y-axis to the curve.
What is the relationship between r of x and r of y in the context of volume calculations?
-r of x represents the distance from the x-axis to the curve when revolving around the x-axis, and r of y represents the distance from the y-axis to the curve when revolving around the y-axis. These are used to determine the radius for volume calculations.
How do you find the volume of the solid formed by rotating the curve y = x^2 around the y-axis from x = 0 to x = 4?
-The volume is calculated using the integral V = pi * ∫[0, 4] (x)^2 dy, with the radius in terms of y being x, which simplifies to V = pi * ∫[0, 4] y^2 dy. The result of this integration is 8pi.
What is the volume of the solid formed by rotating the curve y = x^(2/3) around the y-axis from y = 0 to y = 1?
-The volume is found by integrating the function: V = pi * ∫[0, 1] (y^(3/2))^2 dy, which simplifies to V = pi * ∫[0, 1] y^3 dy. The evaluated integral gives a result of pi/4.
Outlines
📚 Introduction to Calculating Volumes by Rotation
This paragraph introduces the concept of calculating the volume of a solid by rotating a region around the x-axis or y-axis using the disc method and washers method. It explains that the disc method involves taking a cross-sectional area, turning it into a disc by rotation around the x-axis, and then integrating the areas of all these discs to find the total volume. The paragraph also mentions that the volume of a cylinder, which is the shape formed by the rotation, is calculated by multiplying the cross-sectional area (πr^2) by the height (h). The key idea is that the cross-sections used in this technique are circles with an area of πr^2, where r is a function of x when revolving around the x-axis.
🧮 Example: Volume of a Solid Rotated Around the X-Axis
The paragraph presents an example of calculating the volume of a solid formed by rotating the curve y = √x around the x-axis from x = 0 to x = 4. It explains the process of plotting the function, determining the radius as the distance from the curve to the axis of rotation, and setting up the integral for volume calculation. The example demonstrates how to evaluate the integral by finding the antiderivative of the function and applying the limits of integration, resulting in a final volume of 8π cubic units.
📈 Calculating Volumes with Functions Rotated Around the X-Axis
This paragraph continues with another example of finding the volume of a solid generated by rotating the function y = 1/x around the x-axis between the lines x = 1 and x = 3. It explains the process of plotting the function, determining the radius r(x) as the distance from the x-axis to the curve, and setting up the integral for volume calculation. The integral involves the function 1/x^2, which is rewritten as x^(-2), and its antiderivative is found using the power rule. The final answer for the volume is calculated as 2π/3 cubic units.
📊 Volumes of Solids Rotated Around the Y-Axis
The paragraph discusses the process of calculating the volume of solids when a curve is rotated around the y-axis. It provides an example where the curve y = x^2 is bounded by the lines x = 0 and y = 4. The paragraph explains how to graph the function, identify the radius in terms of y (r(y) = x), and set up the integral for volume calculation. The integral involves the function x^2, and its antiderivative is found and evaluated from the bounds, resulting in a volume of 8π cubic units.
🔄 Calculating Volumes with Rotations Around the Y-Axis
The final paragraph focuses on calculating the volume of a solid formed by rotating the curve y = x^(2/3) around the y-axis between the lines x = 0 and y = 1. It explains the process of graphing the function, determining the radius in terms of y (r(y) = x), and solving for x in terms of y. The integral for volume calculation is set up with the function y^(3/2), and its antiderivative is found and evaluated from the bounds, resulting in a final volume of π/4 cubic units.
Mindmap
Keywords
💡Volume
💡Disc Method
💡Washers Method
💡Integration
💡Cross-Sectional Area
💡Cylinder
💡Radius
💡Rotation
💡Curve
💡Solid
💡Antiderivative
Highlights
The video discusses calculating the volume of a shape by rotating it around the x-axis or y-axis using the disc method and washers method.
The disc method involves taking a cross-sectional area and turning it into a disc by rotating the region around an axis, forming a shape similar to a cylinder.
The volume of a cylinder is calculated by multiplying the cross-sectional area (pi r squared) by the height.
To find the volume of a solid, one must integrate the cross-sectional area from one point to another on the axis of rotation.
When revolving around the x-axis, the radius is a function of x and the volume is found by integrating pi r squared dx from a to b.
For revolving around the y-axis, the volume is calculated using pi times the integration of r of y squared dy from c to d, where r is a function of y.
An example is provided where the function y equals the square root of x is rotated about the x-axis between x equals 0 and x equals 4.
The radius for the square root of x function is found by plotting the function and determining the distance from the curve to the x-axis.
The volume calculation for the square root of x function involves integrating pi times the square root of x squared from 0 to 4.
The integral of the square root of x squared is x squared over 2, and the final volume is found by evaluating this from 0 to 4, resulting in 8 pi.
Another example involves rotating the function y equals 1/x about the x-axis between x equals 1 and x equals 3.
The radius for the 1/x function is the function itself, 1/x, and the volume is found by integrating pi times 1/x squared from 1 to 3.
The integral of 1/x squared is -1/x, and the final volume is calculated by evaluating this from 1 to 3, resulting in 2 pi/3.
The video also covers examples of finding the volume when rotating around the y-axis, such as with the function y equals x squared between the lines x equals 0 and y equals 4.
For the x squared function, the radius in terms of y is x, and the volume is found by integrating pi times x squared from 0 to 4.
The final volume for the x squared function, when rotated about the y-axis, is 8 pi after integrating and evaluating the function.
A final example involves rotating the function y equals x to the 2/3 power about the y-axis between the lines x equals 0 and y equals 1.
The radius in terms of y for the x to the 2/3 power function is y to the 3/2 power, and the volume is found by integrating pi times y to the 3/2 power from 0 to 1.
The integral of y to the 3/2 power is y to the 4/4 power over 4, and the final volume is pi over 4 after evaluation.
Transcripts
Browse More Related Video

Solid of Revolution (part 5)

Washer method rotating around vertical line (not y-axis), part 1 | AP Calculus AB | Khan Academy

Calculus 1 Lecture 5.2: Volume of Solids By Disks and Washers Method

Calculating Volume by Cylindrical Shells
Calculating the Volume of a Solid of Revolution by Integration

Solid of Revolution (part 2)
5.0 / 5 (0 votes)
Thanks for rating: