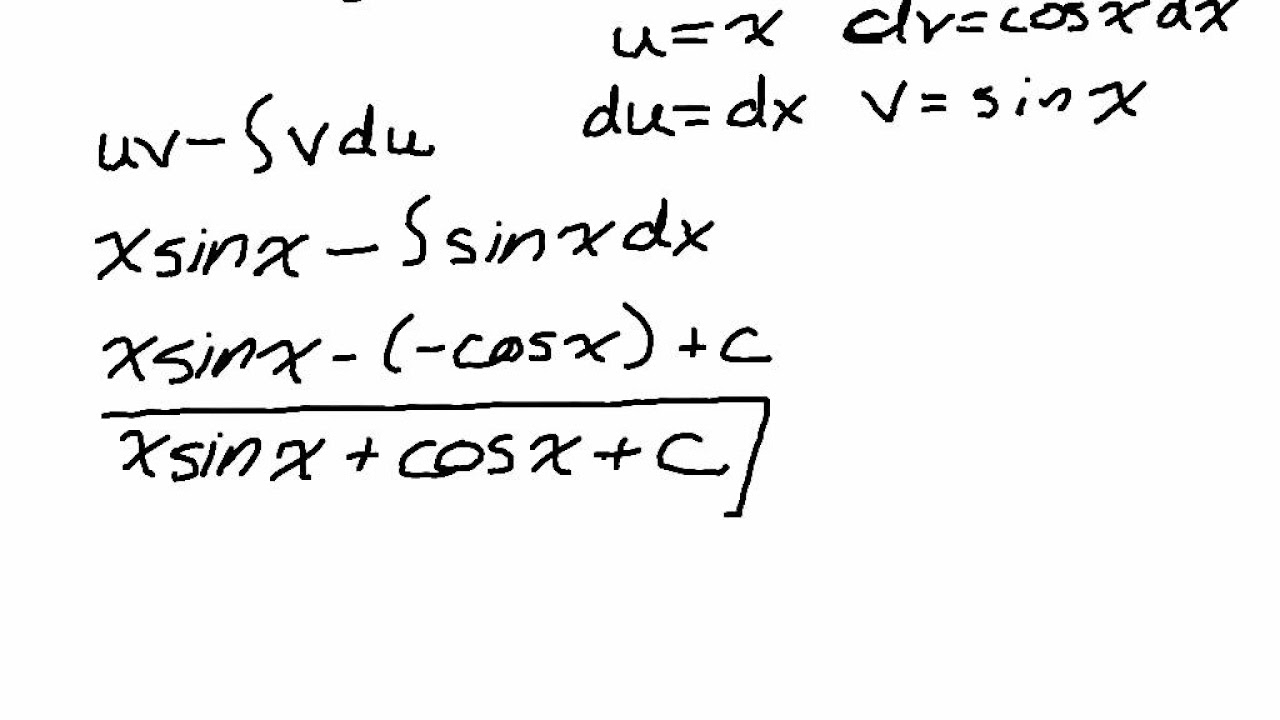Integration By Parts
TLDRThe transcript outlines a comprehensive guide to solving indefinite integrals using integration by parts. It demonstrates the process through various complex examples, such as integrating products of functions like x and e^x, x*sin(x), x^2*ln(x), and natural log functions. The method involves selecting appropriate u and dv, calculating derivatives and integrals, and applying the formula u*v - v*du. The examples showcase the application of chain rule, moving constants, and simplifying expressions to reach the final answer, which includes a constant of integration, c.
Takeaways
- 📚 Integration by parts is a technique used to find the indefinite integral of certain functions, where the integral of a product of two functions is expressed in terms of the product of the first function and the integral of the second function.
- 🌟 When applying integration by parts, it's useful to set the first function as 'u' if its derivative is simpler or a constant, making the integration process easier.
- 🔄 The formula for integration by parts is ∫(uv)'dx = uv - ∫v(du)dx, where 'u' and 'dv' are chosen parts of the integrand.
- 📈 In the case of ∫x * e^x dx, setting u = x and dv = e^x dx results in the integral being simplified to x * e^x - ∫e^x dx, with the latter being e^x + C.
- 🧮 For the integral of x * sin(x) dx, u = x and dv = sin(x) dx leads to the result of -x * cos(x) + sin(x) + C after applying integration by parts.
- 📊 When integrating x^2 * ln(x), it's beneficial to set u = ln(x) and dv = x^2 dx, which results in the integral 1/3 * x^3 * ln(x) - 1/9 * x^3 + C.
- 🤔 For anti-derivative of ln(x), integration by parts can be applied by setting u = ln(x) and dv = dx, leading to the result x * ln(x) - x + C.
- 🌐 For the integral of x^2 * sin(x), a two-step integration by parts process is required, resulting in the expression -x^2 * cos(x) + 2x * sin(x) + 2 * cos(x) + C.
- 💡 When dealing with integrals of the form x^2 * e^x, it's necessary to use integration by parts twice, ultimately yielding x^2 * e^x - 2 * x * e^x + 2 * e^x + C.
- 📝 For the integral of ln(x)^2 dx, setting u = ln(x)^2 and dv = dx allows us to find the integral as x * ln(x)^2 - 2 * x * ln(x) + 2 * x + C.
- 🌟 The strategy of moving constants to the front and factoring out common terms can simplify the process of solving complex integrals, as seen in the example of ∫e^(3x) * cos(4x) dx.
Q & A
What is the main integration technique used in the script to find indefinite integrals?
-The main integration technique used in the script is Integration by Parts.
How is Integration by Parts defined and when is it best to use it?
-Integration by Parts is defined as the method where the integral of u dv is equal to u times v minus the integral of v du. It is best to use when dealing with products of two functions, especially when one of the functions is easily integrable and the other is a simple power function.
What function does the script use as an example to demonstrate Integration by Parts?
-The script uses the function x times e^x as an example to demonstrate Integration by Parts.
How does the script suggest choosing u and dv in Integration by Parts?
-The script suggests choosing u to be the function that becomes simpler or easier to integrate when differentiated, and dv to be the remaining function.
What is the final result of the Integration by Parts example with x times e^x?
-The final result is x times e^x minus the integral of e^x dx, which simplifies to x times e^x plus C, where C is the constant of integration.
What is the significance of the constant C in the context of indefinite integrals?
-The constant C represents the arbitrary constant of integration that is added to the antiderivative to account for the infinite number of possible antiderivatives that exist for a given derivative.
How does the script handle the integration of more complex functions like x squared times ln x?
-The script handles the integration of complex functions like x squared times ln x by using Integration by Parts multiple times and strategically choosing u and dv to simplify the integration process.
What is the final result of the integration of x squared ln x?
-The final result is one third times x cubed times ln x minus one ninth times x cubed plus C.
How does the script approach the integration of products involving sine and cosine functions?
-The script approaches the integration of products involving sine and cosine functions by using Integration by Parts, carefully selecting u and dv, and using the derivatives and antiderivatives of these trigonometric functions.
What is the final result of the integration of x squared times sine x?
-The final result is negative x squared times cosine x plus 2x times sine x plus 2 times cosine x plus C.
How does the script demonstrate the use of Integration by Parts for repeated integration?
-The script demonstrates the use of Integration by Parts for repeated integration by applying the method multiple times to the same or similar integral expressions, showing how to break down complex integrals into simpler forms.
Outlines
📚 Introduction to Integration by Parts
This paragraph introduces the concept of integration by parts, a technique used to find the indefinite integral of functions. It explains the formula (∫udv = uv - ∫vdu) and provides a step-by-step process for selecting u and dv. The paragraph demonstrates the application of this method on the function x*e^x and shows how to determine the appropriate functions for u and dv. The integration by parts is performed, resulting in the final answer x*e^x - ∫e^x dx, which simplifies to x*e^x + C, where C is the constant of integration. The paragraph also presents another example, the integration of x*sin(x) dx, and explains how to apply integration by parts to find the antiderivative.
🧠 Solving Complex Integrals Using Integration by Parts
This paragraph delves into more complex integrals and the application of integration by parts. It covers the integration of functions such as x^2*ln(x) and natural log of x, explaining the selection of u and dv in each case. The paragraph demonstrates the step-by-step process of integrating x^2*ln(x) to obtain the result (1/3)x^3*ln(x) - (1/9)x^3 + C. It also tackles the integral of x^2*sin(x) by applying integration by parts twice and arriving at the final answer -x^2*cos(x) + 2x*sin(x) + 2*cos(x) + C. The paragraph emphasizes the importance of understanding the technique and being able to adapt it to various functions.
🌟 Advanced Integration by Parts
This paragraph presents more advanced applications of integration by parts, focusing on problems where the integral cannot be easily found using basic techniques. It covers the integration of x^2*e^x and demonstrates the need for applying integration by parts multiple times. The paragraph explains the process of selecting u and dv, integrating, and simplifying to obtain the final result x^2*e^x - 2xe^x + 2e^x + C. It also addresses the integral of ln(x)^2 and shows how to use integration by parts effectively to arrive at the solution x*ln(x^2) - x^2/2 + C. The paragraph highlights the importance of mastering integration by parts for solving complex integrals in calculus.
📈 Integration of Trigonometric and Exponential Functions
This paragraph focuses on the integration of trigonometric and exponential functions using integration by parts. It explains the process of integrating x^2*e^x*sin(x) and demonstrates how to simplify the expression using integration by parts. The paragraph shows the step-by-step calculation, which leads to the final result (1/2)e^(x)*sin(x) - (1/2)e^(x)*cos(x) + C. It also covers the integration of ln(x)^2/x and explains the method of rewriting the problem and applying integration by parts to find the antiderivative. The paragraph emphasizes the importance of understanding the properties of the functions being integrated and the correct application of integration techniques.
🔢 Definite Integrals and Factoring
This paragraph discusses the calculation of definite integrals and the use of factoring to simplify the process. It presents the problem of finding the definite integral of e^(3x)*cos(4x) and illustrates how to apply integration by parts and factor out common terms. The paragraph shows the step-by-step integration process, leading to the result (1/3)e^(3x)*cos(4x) + (4/9)e^(3x)*sin(4x) + C. It also emphasizes the importance of factoring out common factors, such as e^(3x) and 1/3, to simplify the expression and make it easier to evaluate the definite integral. The paragraph highlights the application of integration techniques in solving complex problems and the significance of factoring in obtaining a simplified result.
Mindmap
Keywords
💡Indefinite Integral
💡Integration by Parts
💡Derivative
💡Antiderivivative
💡Constants
💡Chain Rule
💡Power Rule
💡Trigonometric Functions
💡Exponential Functions
💡Integration Techniques
💡Arbitrary Constant
Highlights
The use of integration by parts to find the indefinite integral of x times e^x.
Setting u = x and dv = e^x dx simplifies the integration process.
The integral of u dv is u times v minus the integral of v du.
For the integral of x times sine x, u = x and dv = sine x dx are chosen.
Integration by parts can be applied multiple times for complex integrals.
The integral of x^2 ln x is found by setting u = x^2 and dv = ln x dx.
The use of the chain rule is necessary for differentiating ln x^2.
Integration by parts is a powerful tool for integrals involving products of functions.
The integral of the natural log of x is found using u = ln x and dv = dx.
For the integral of x^2 sine x, integration by parts is applied twice.
The integral of x squared e^x involves setting u = x^2 and dv = e^x dx, and using integration by parts twice.
The integral of ln x^2 involves setting u = ln x^2 and dv = dx, and using the chain rule.
The integral of ln x to the seventh power is simplified by rewriting it as 7 ln x.
The integral of e^x sine x is found by setting u = sine x and dv = e^x dx, and applying integration by parts.
The integral of ln x squared divided by x is solved by rewriting the expression and setting appropriate u and dv.
The definite integral of e^(3x) cosine(4x) is found by applying integration by parts and simplifying the expression.
Integration by parts is a versatile technique that can handle a wide range of integrals, including those involving trigonometric and exponential functions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: